3. По формуле обращения (обратного преобразования Фурье) находим

реакцию

(10)

На практике для аналитически заданных x(t) и W(j) операции (8) и (10) выполняются с помощью таблиц соответствия между оригиналами и изображениями. Если нет аналитических выражений или они сложны, то прибегают к численным методам интегрирования (8), (10) с помощью ЭВМ.

Характер преобразования входного сигнала звеном или системой определяется частотной передаточной функцией или соответствующими ей частотными характеристиками. Виды частотных характеристик тесно связаны с формами записи комплексных чисел, поскольку для =const частотная передаточная функция является комплексным числом. Существует три формы записи комплексного числа

1. Обычная форма W=W_x+jW_y, j= 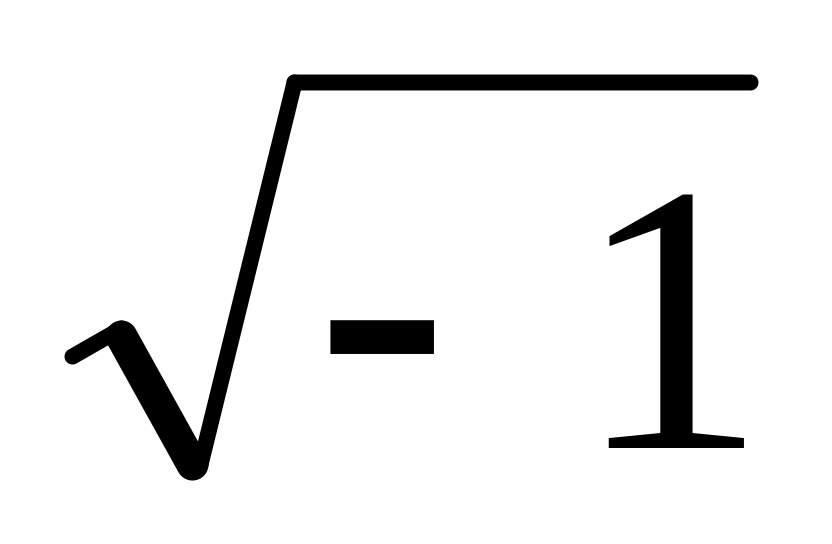; (11)

2. Тригонометрическая форма W=A(cos+jsin); (12)

3. Показательная форма W=Ae^j (13)

Комплексное число представляет точку на комплексной плоскости с действительной и мнимой частями W_x, W_y. Точке соответствует вектор с длиной (модулем) А и аргументом  (рис. 1).

Положительное направление отсчета углов – против часовой стрелки. Из (11) –(13) и рис. 1 вытекают соотношения

W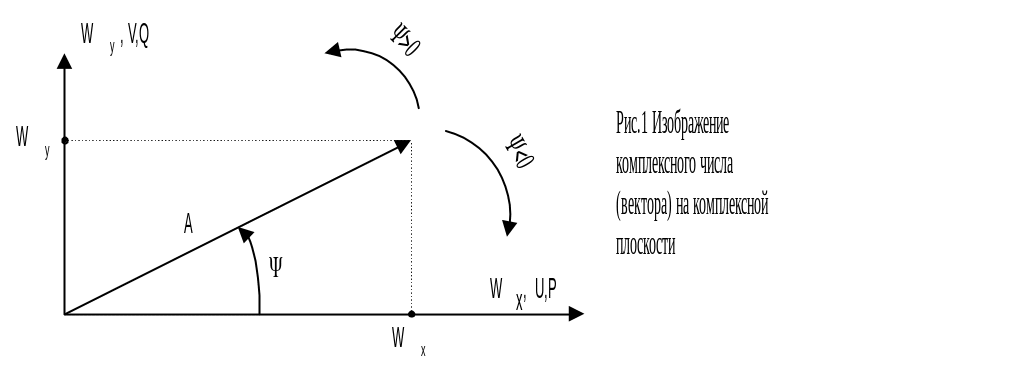 _x=Acos; ;

W_y=Asin; . (14)

Пусть W₁=A₁e^j1 и W₂=A₂e^j2

Тогда _; (15)

, (16)

т. е. при перемножении комплексных чисел их модули перемножаются, а аргументы складываются. В случае деления комплексных чисел их модули делятся, а аргументы вычитаются.

Заметим также, что произведение комплексно-сопряженных чисел дает квадрат модуля, т.е.

WW^*=(W_x+jW_y) (W_x-jW_y)=W_x²+W_y²=A². (17)

Если имеем дробь

, (18)

то для определения вещественной и мнимой частей надо умножить числитель и знаменатель (18) на число комплексно-сопряженное знаменателю. В результате получим

, (19)

где

. (20)

Заметим, что W_y (20) не содержит мнимой единицы, имеющейся в записи (19). Если нужно найти модуль и аргумент числа (19), то следует воспользоваться правилом (16), а не искать W_Х, W_y по (20) с последующим нахождением А и  по (14).

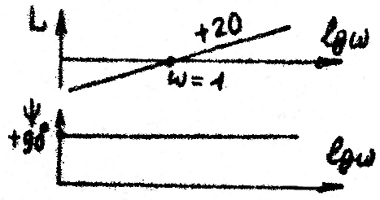
Перечислим теперь основные частотные характеристики (рис.2).

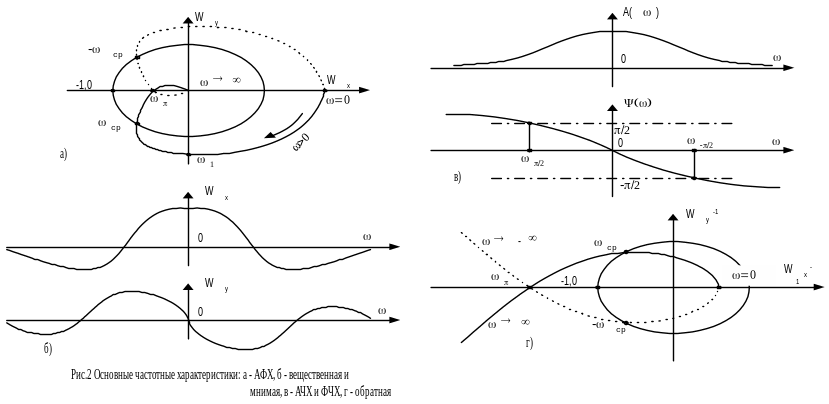
Наиболее широкое применение нашли логарифмические характеристики:

Логарифмическая амплитудная характеристика (ЛАХ):

L()=20lgA()=20lgW(j). (22)

Логарифмическая фазовая характеристика (ЛФХ):

()=argW(j). (23)

Амплитуда измеряется в децибелах, фаза – в градусах, а по оси частот откладывается частота в логарифмическом масштабе, т. е. lg. Для удобства следует делать разметку оси абсцисс непосредственно в значениях  (рад/с), например, с помощью делений на логарифмической линейке (рис. 3).

Если ₂/₁=10, то расстояние между частотами равно одной декаде (lg10=I), если ₂/₁=2, то расстояние равно одной октаве. Так как lg(=0)=-, то точка =0 находится на бесконечности слева. Поэтому ось ординат проводят в любом месте с таким расчетом, чтобы на график попал интересующий диапазон частот. Так как 20lg1=0, то L()>0, если А()>1 и L()<0, если А()<1. Если А()0, то L().

З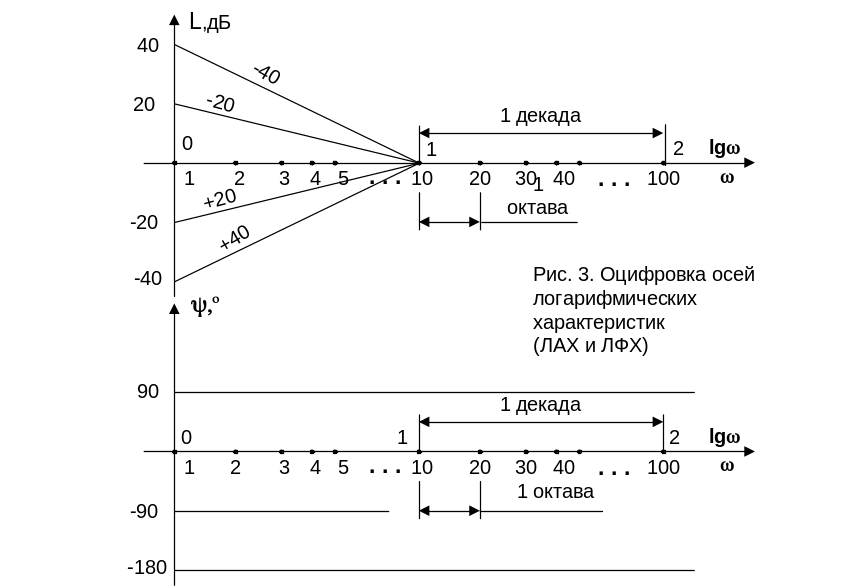 аметим, что реальные (физически реализуемые) звенья и системы имеют ограниченную полосу пропускания, т. е. А()0 при 0 или W(j)0 при . Для выполнения этого условия в формулах (1), (6), (7) должны иметь n>m, т. е. степень знаменателя передаточной функции должна быть больше степени числителя. Тем не менее рассматриваются звенья, для которых условие физической осуществимости не выполняется. Это правомерно в определенном диапазоне частот. Если спектр сигнала на входе звена выходит за пределы этого диапазона, то возникнут искажения в реакции, не предусмотренные передаточной функцией звена. Попутно остановимся на физическом смысле отрицательных частот. Они являются математической абстракцией и их необходимость можно пояснить с помощью формулы (10), которая представляет оригинал – вещественную функцию y(t) в виде суммы (интеграла) элементарных гармоник . Элементарную гармонику можно изобразить на диаграмме в виде вектора, вращающегося против часовой стрелки со скоростью . Сумма всех векторов должна быть действительным числом. Для этого каждому элементарному вектору, вращающемуся против часовой стрелки (0) должен соответствовать аналогичный (симметричный) вектор, вращающийся по часовой стрелке, т.е. с отрицательной скоростью (-0). Сумма двух элементарных векторов (по правилу параллелограмма) дает вектор, направленный по действительной оси, т.е. действительное число (рис.4).

П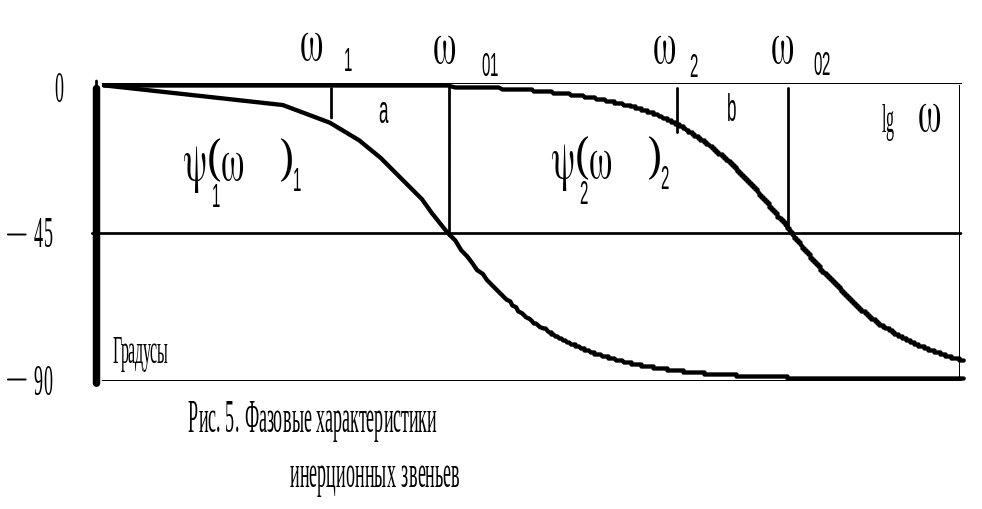 оэтому сумма всех пар элементарных векторов, т. е. y(t) будет действительным числом.

Х арактеристики основных (типовых) звеньев приведены в табл. 1.

Логарифмические характеристики звеньев Таблица 1.1

№ п/п	Название звена		ЛАХ, ЛФХ
1	Идеальное интегрирующее
2	Инерционное
3	Колебательное
4	Идеальное дифференцирующее
5	Форсирующее
6	Обратное колебательному

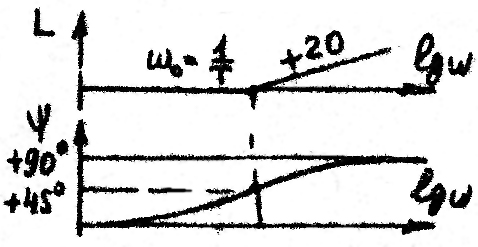
Рассмотрим ЛФХ двух инерционных звеньев с сопрягающими частотами (рис. 5). Вычислим сдвиги по фазе на частотах ₁ и ₂ для обоих звеньев . Если , то ₁=₂.

Но первое равенство означает, что расстояния между соответствующими частотами в логарифмическом масштабе равны, т. е. а=b. Поэтому, если сместить первую кривую вправо вдоль оси частот до совмещения точек обеих кривых с ординатами -45, то кривые совпадут.. Это позволяет при построении фазовых характеристик инерционных и обратных им (форсирующих) звеньев пользоваться одним шаблоном, построенным, например, для звена с 1/с.

Значения () инерционного звена для построения шаблона приведены в табл. 2. Для построения ЛФХ правее точки сопряжения можно учесть, что она кососимметрична относительно точки (₀, -45).

ЛФХ инерционного звена [град] Таблица 2

	0.01	0.06	0.10	0.20	0.40	0.60	0.80	1.0	2.0	4.0	6.0	10	30
-	0.6	3.4	5.7	11.3	21.8	31	38.7	45	63.4	76	80.5	84	8