
Задачи для самостоятельного решения
I. Проверить, образует ли метрическое пространство.
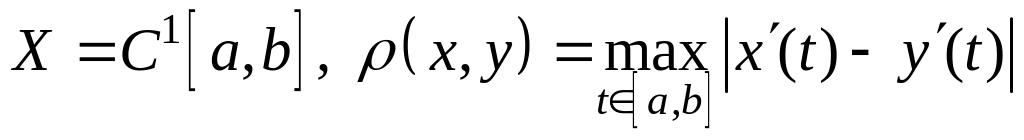 ;
;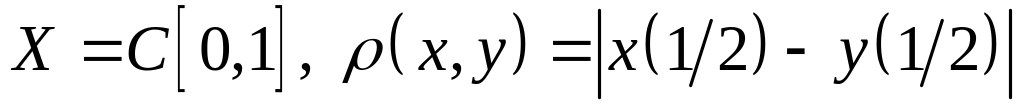 ;
;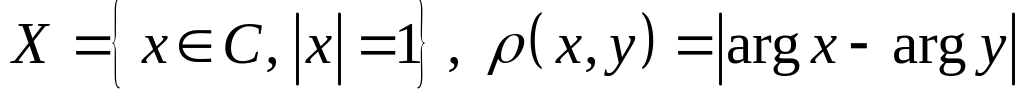 ;
; ;
;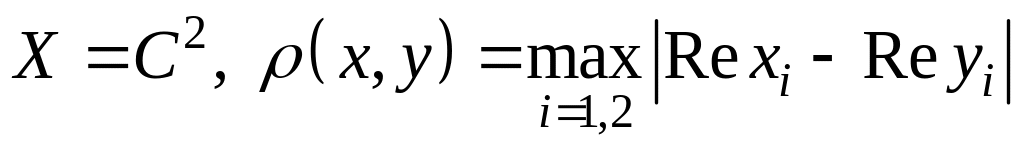 ;
;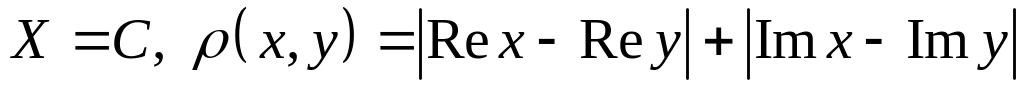 ;
; ;
;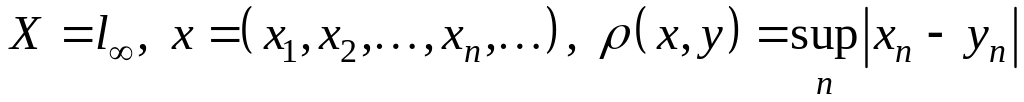 ;
; ;
;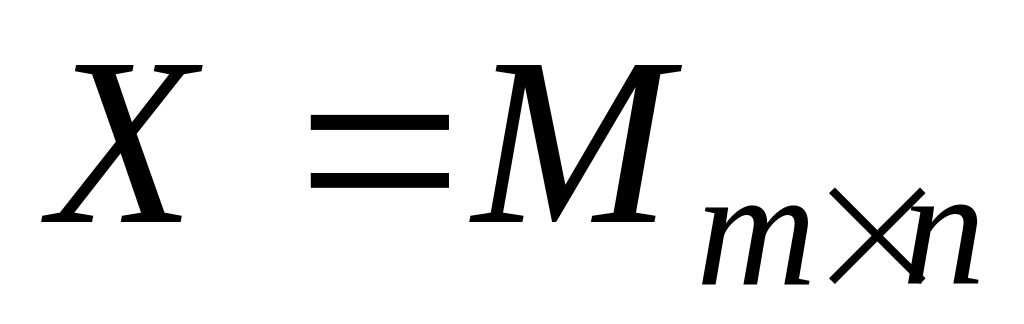 -
матрицы размером
-
матрицы размером
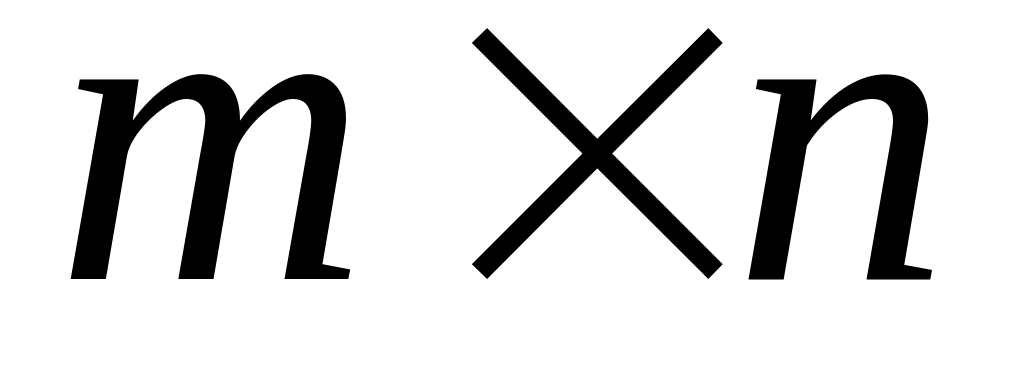 ,
,
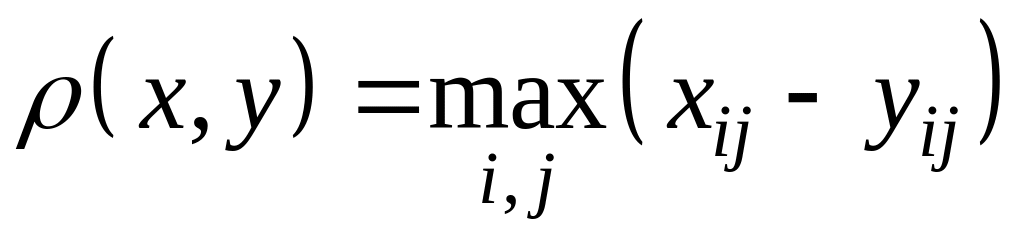 ;
; ;
;- сфера в трехмерном пространстве
 ,
- длина хорды, соединяющей точки
,
- длина хорды, соединяющей точки
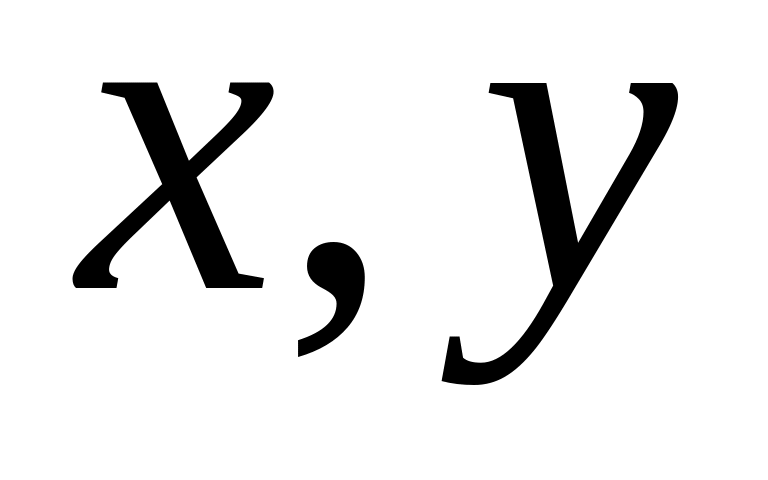 ;
;- сфера в трехмерном пространстве , - длина кратчайшей дуги большого круга, проходящего через точки ;
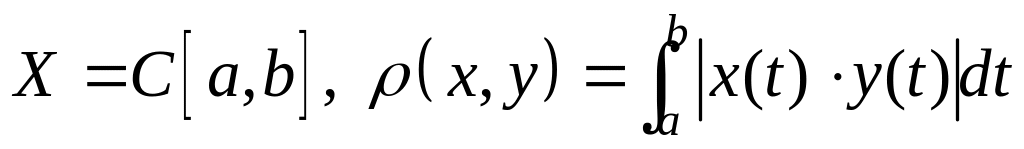 ;
;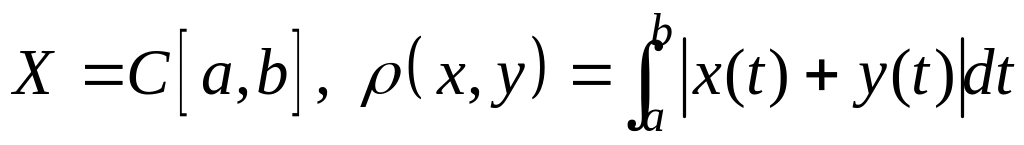 ;
; ;
;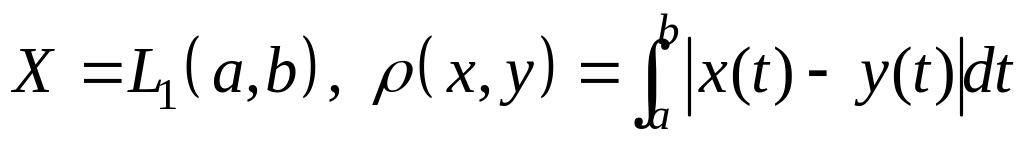 ;
;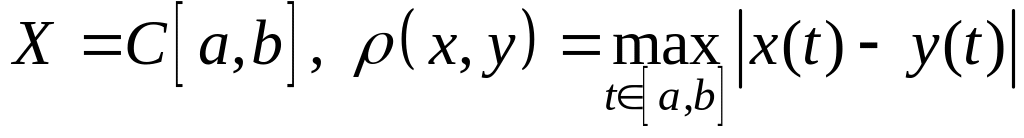 ;
;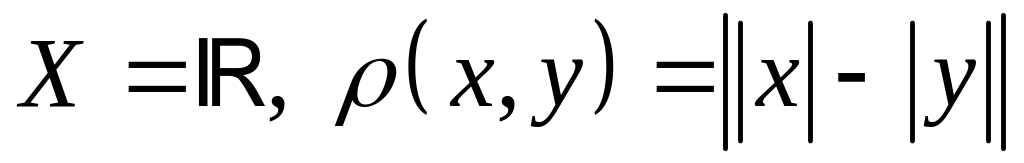 ;
;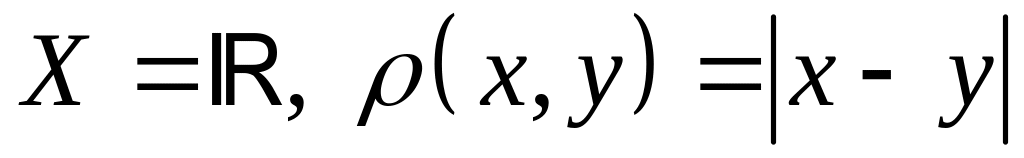 .
.
II. Проверить, можно ли ввести норму указанным образом.
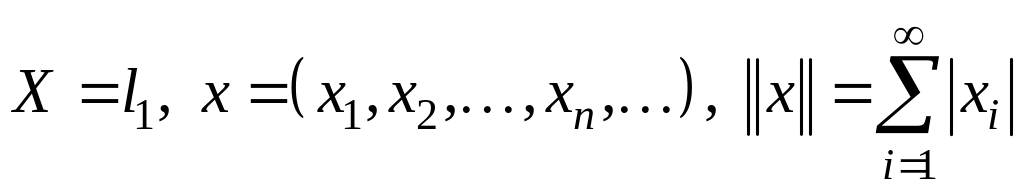 ;
; ;
;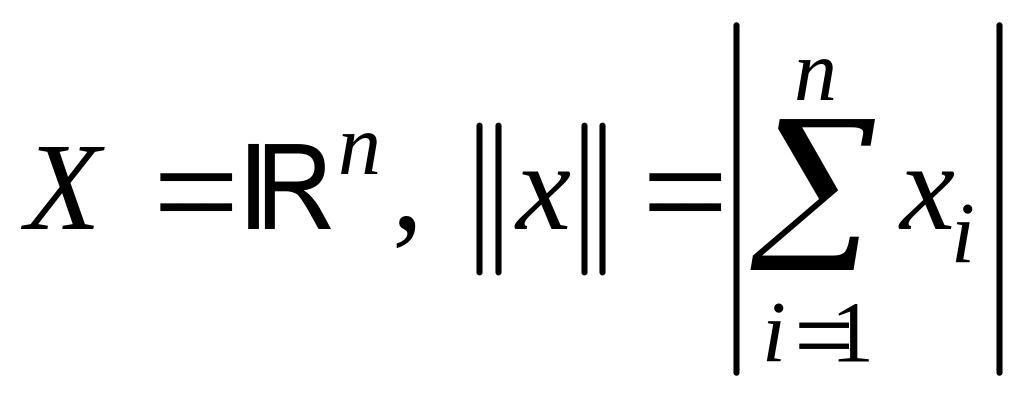 ;
;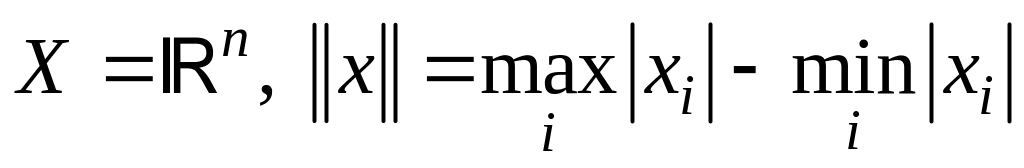 ;
; ;
;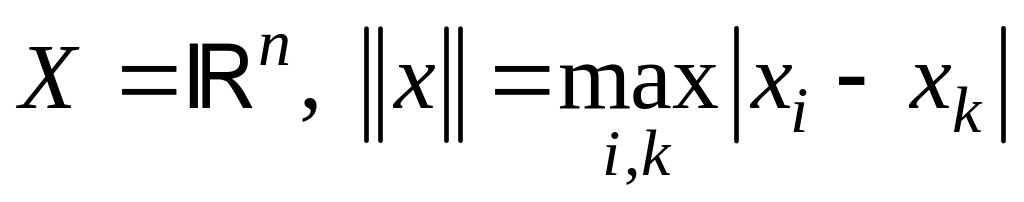 ;
; ;
;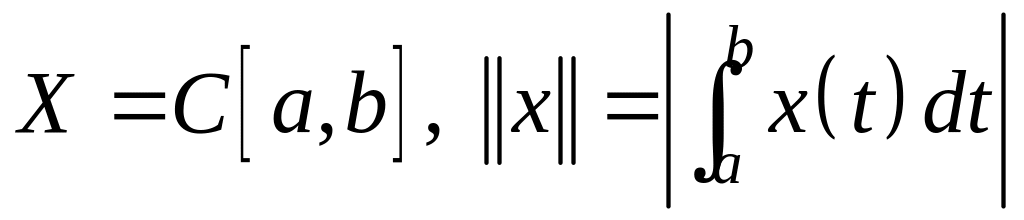 ;
; ;
;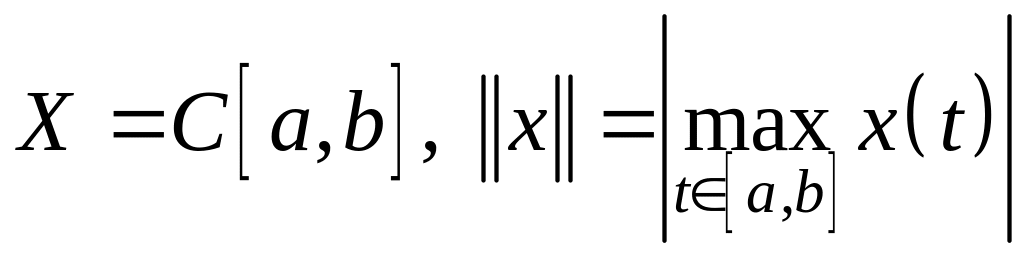 ;
; ;
;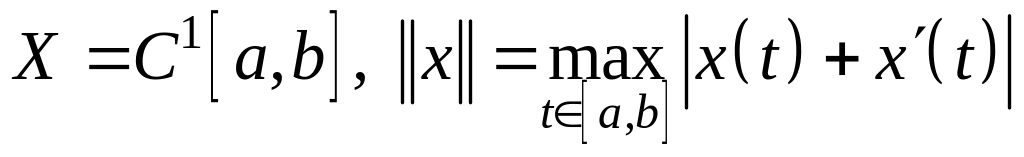 ;
;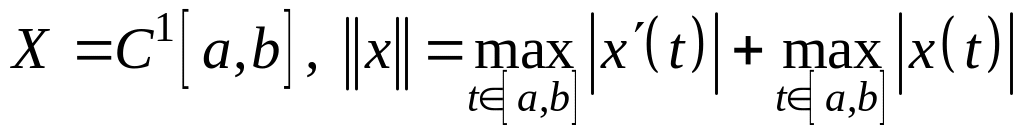 ;
;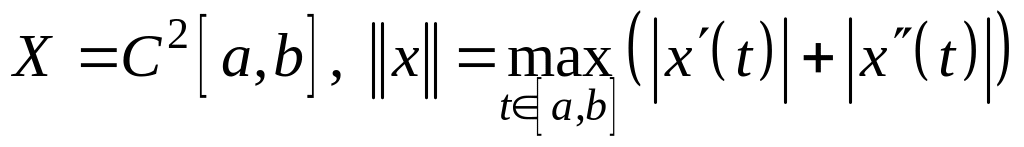
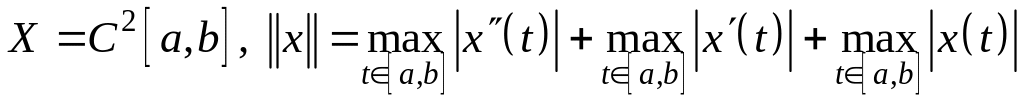 ;
;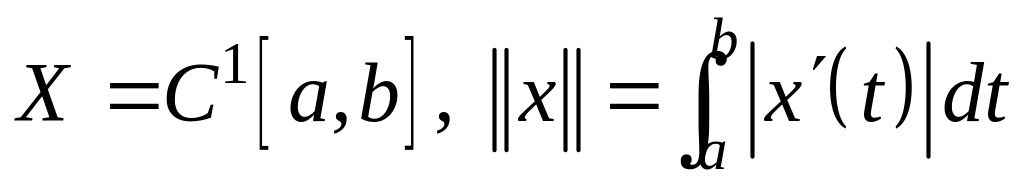 ;
;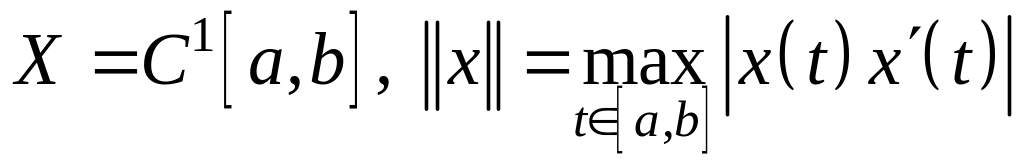 ;
;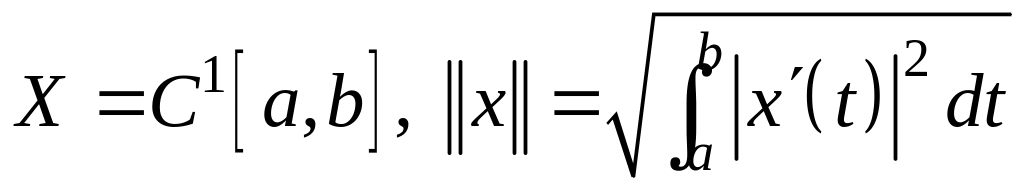 ;
;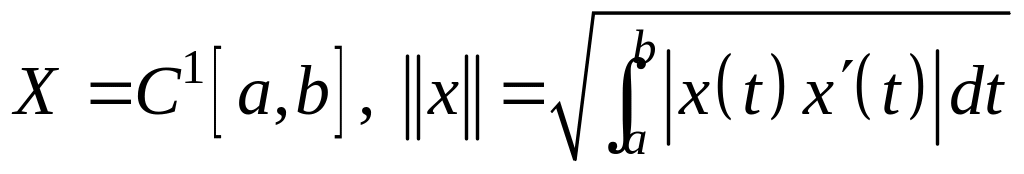 ;
;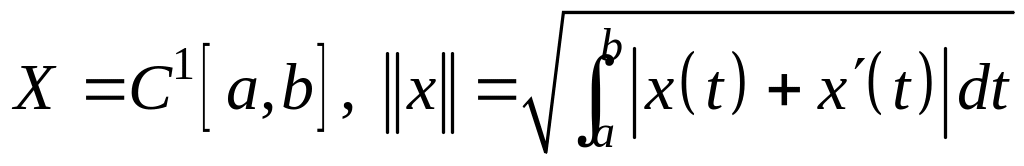 .
.
III. В пространстве найти проекцию элемента на подпространство, порожденное .
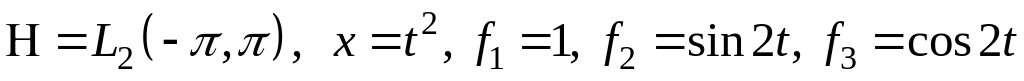 ;
;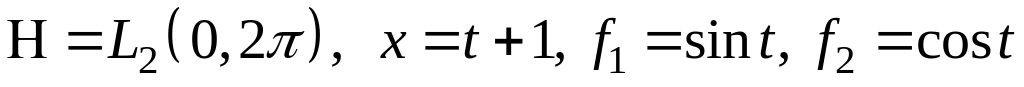 ;
;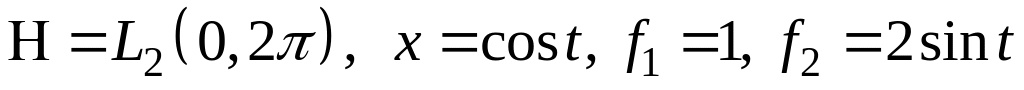 ;
;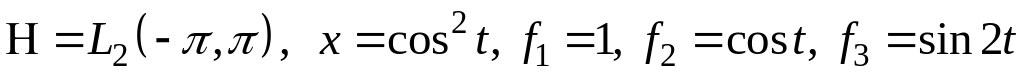 ;
;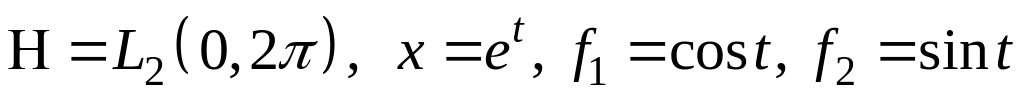 ;
; ;
;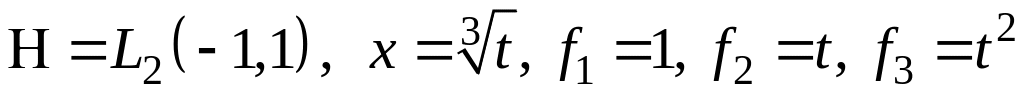 ;
;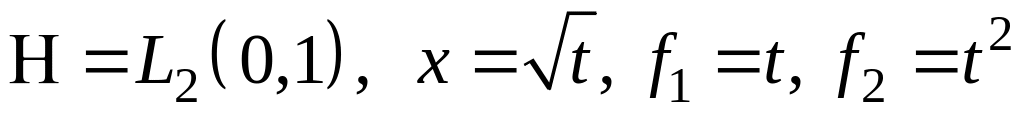 ;
;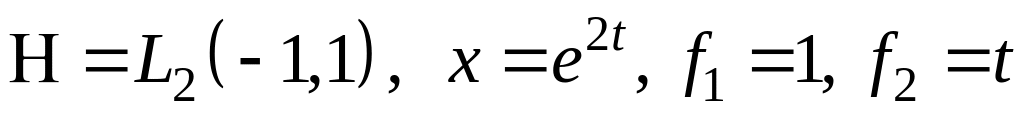 ;
; ;
;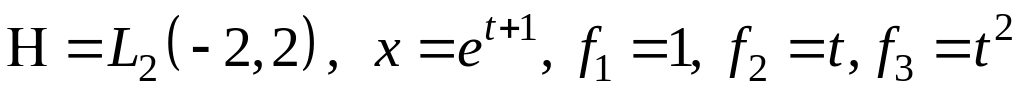 ;
;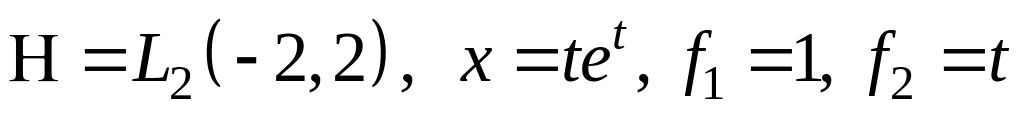 ;
;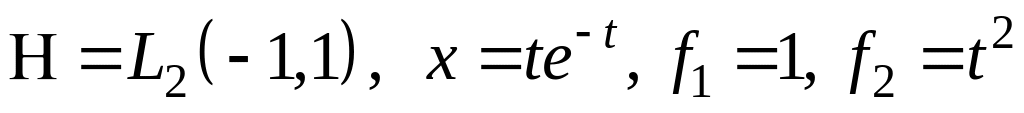 ;
;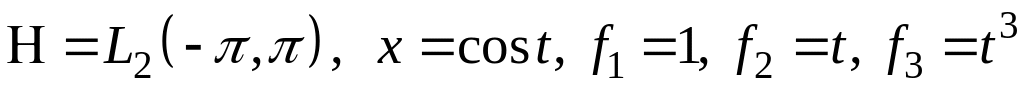 ;
;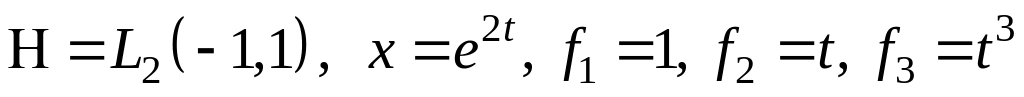 ;
;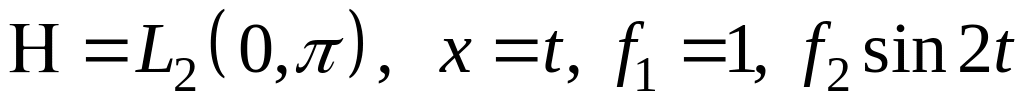 ;
;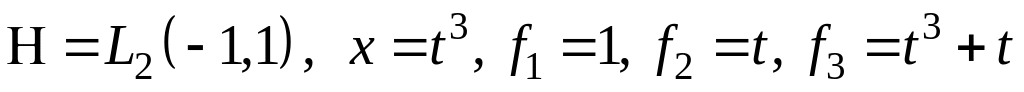 ;
;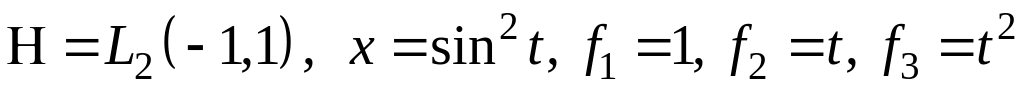 ;
;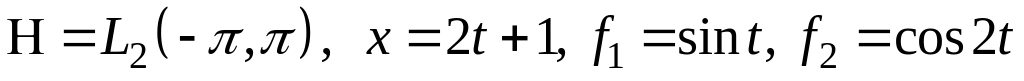 ;
;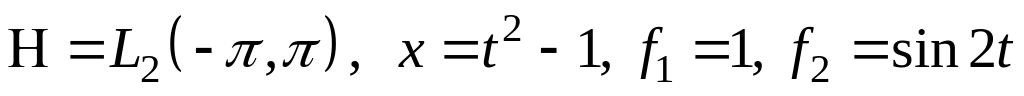 .
.
IV. Показать, что оператор ограничен в пространстве , и найти его норму.
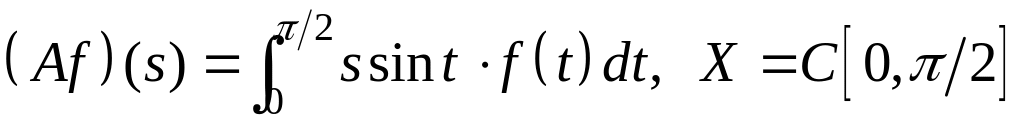 ;
;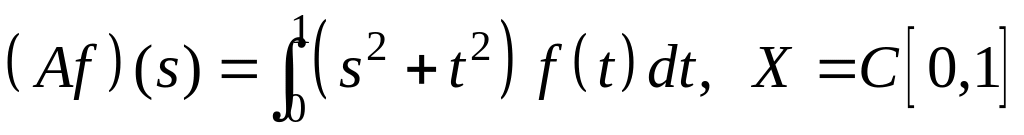 ;
; ;
;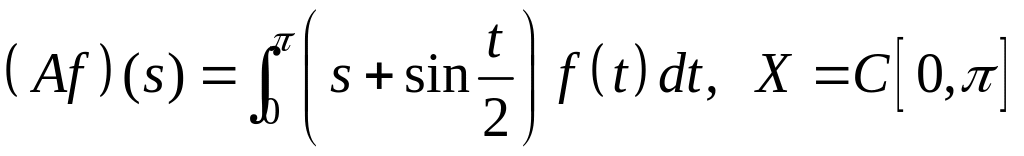 ;
;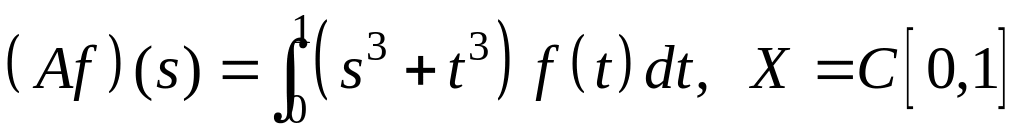 ;
;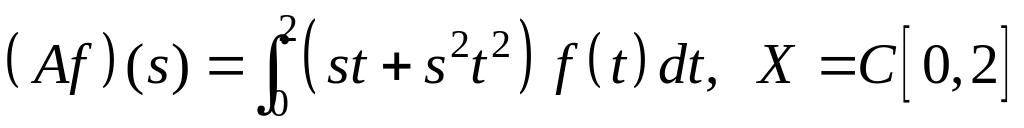 ;
; ;
;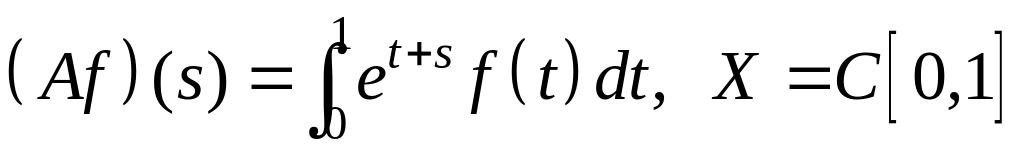 ;
;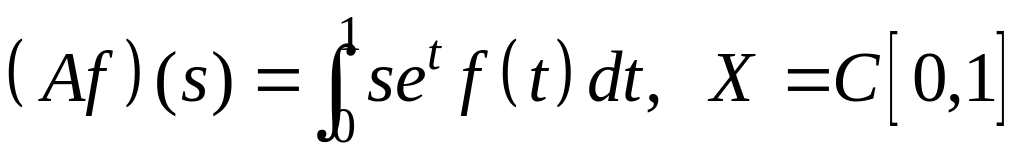 ;
;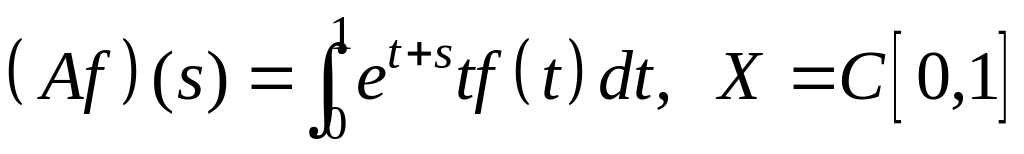 ;
;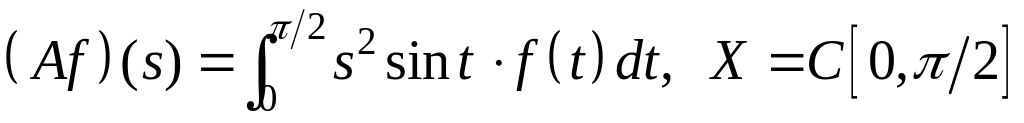 ;
; ;
;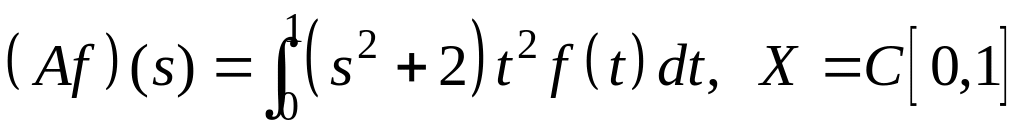 ;
;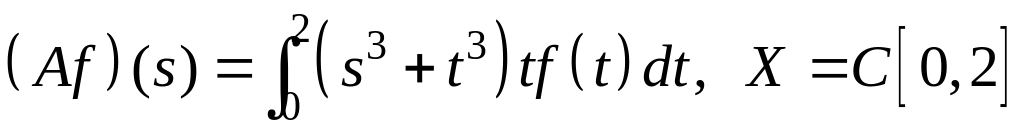 ;
; ;
;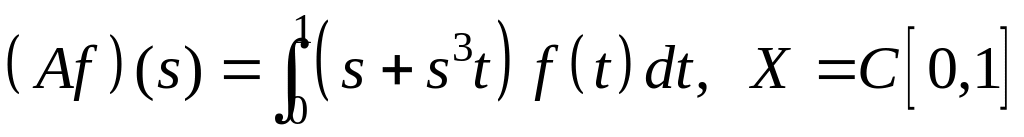 ;
;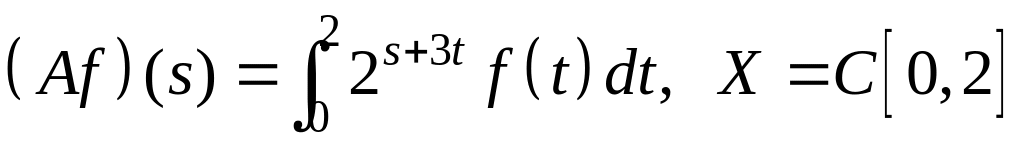 ;
;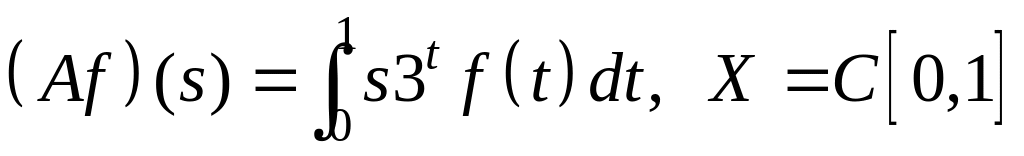 ;
;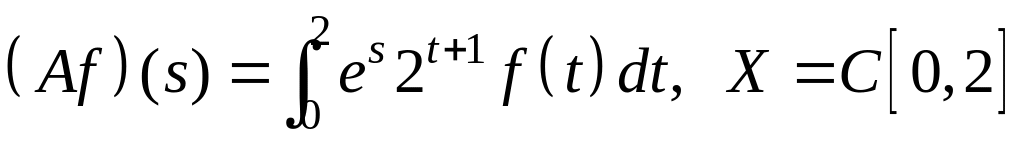 ;
;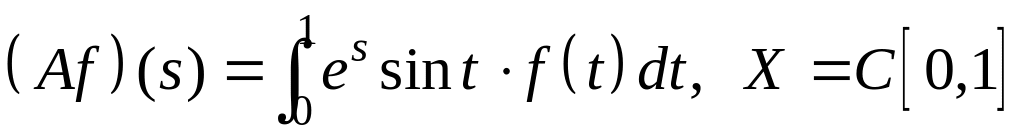 .
.
V.
Найти точечный спектр и собственные
функции оператора A
в
![]() .
.
 ;
;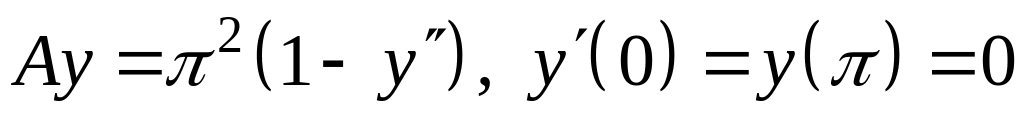 ;
;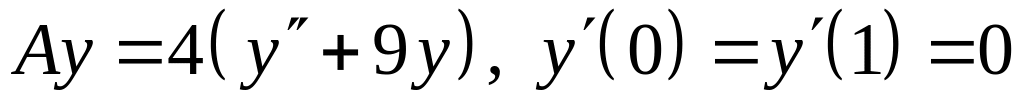 ;
;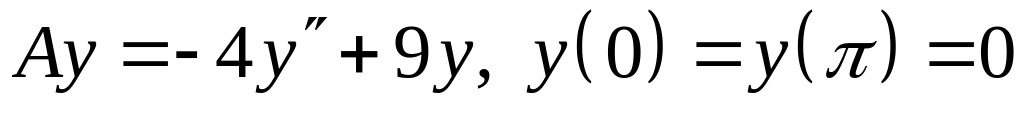 ;
;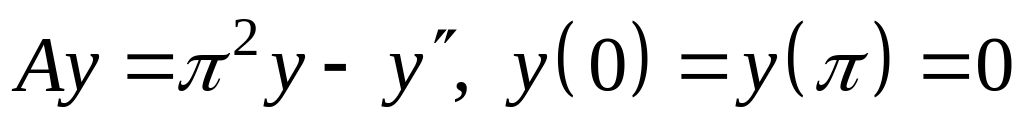 ;
;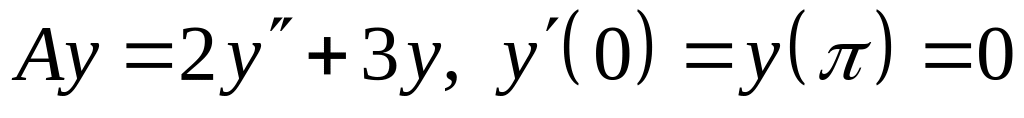 ;
;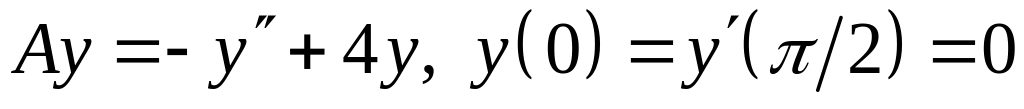 ;
; ;
;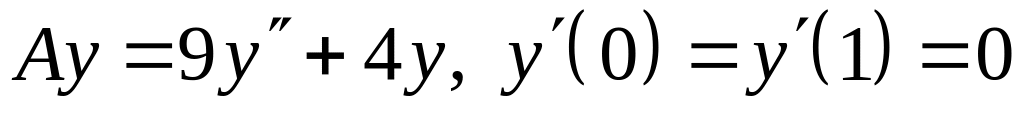 ;
;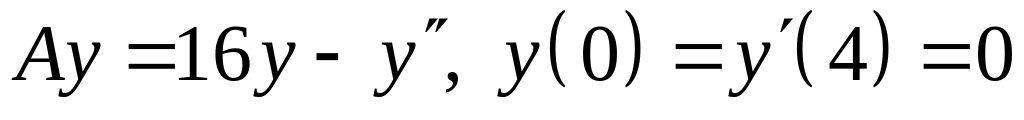 ;
;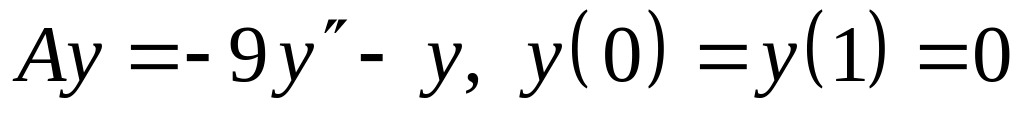 ;
;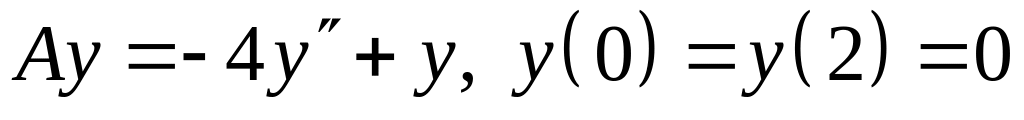 ;
; ;
; ;
;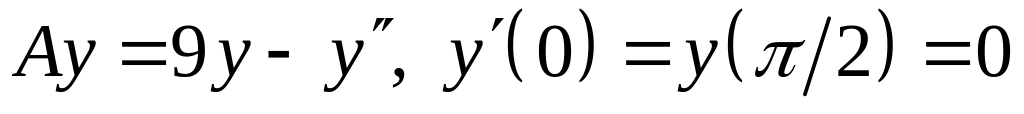 ;
;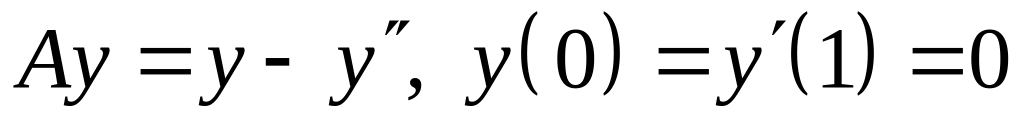 ;
;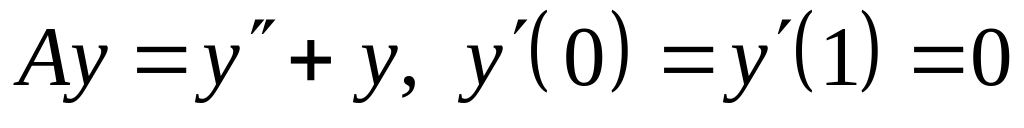 ;
; ;
;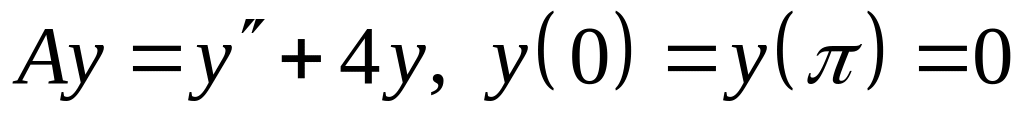 ;
;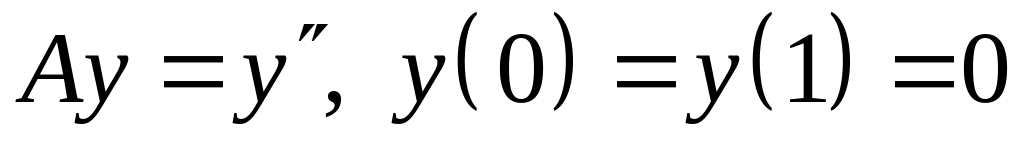 .
.
VI. Проверить, является ли оператор двукратного дифференцирования , определенный в комплексном пространстве на дважды непрерывно дифференцируемых функциях, удовлетворяющих указанным граничным условиям, симметричным. Каким граничным условиям удовлетворяют функции из области определения сопряженного оператора?
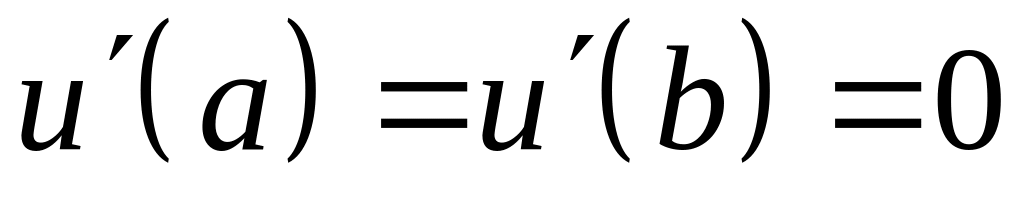 ;
;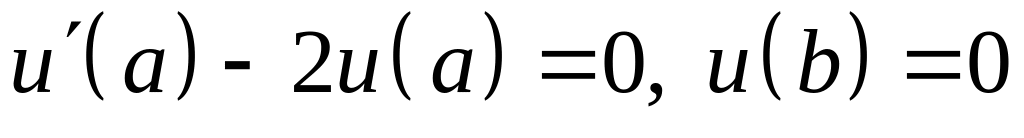 ;
;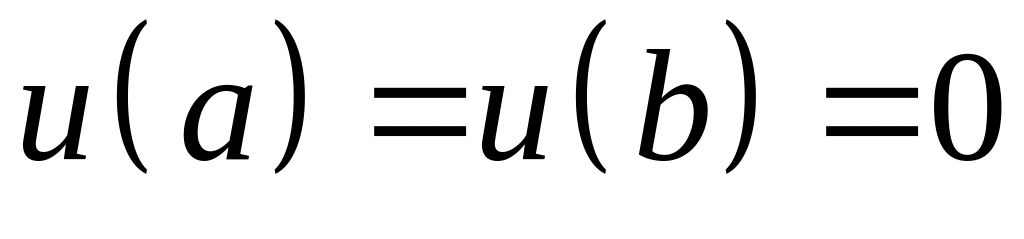 ;
;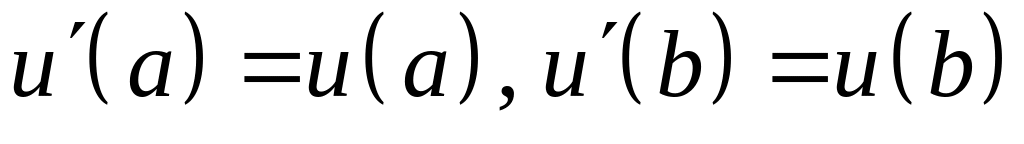 ;
; ;
; ;
; ;
;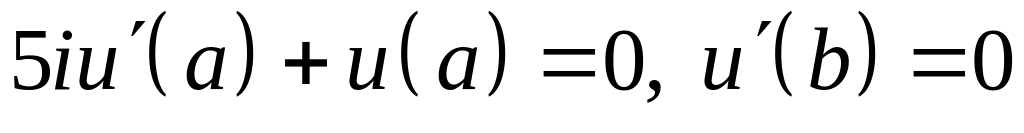 ;
;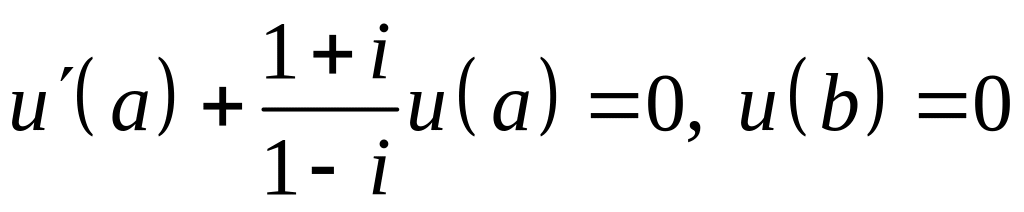 ;
;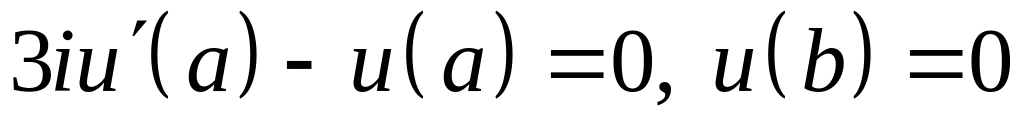 ;
;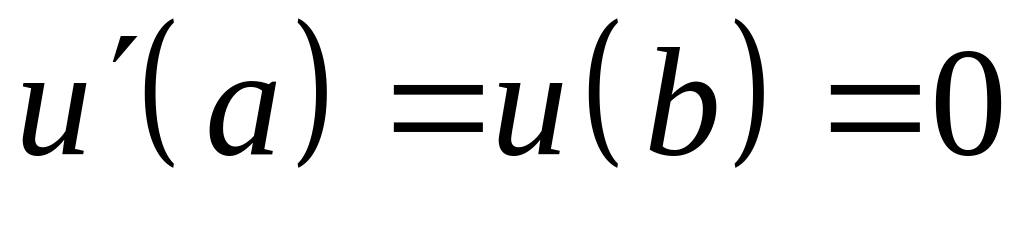 ;
;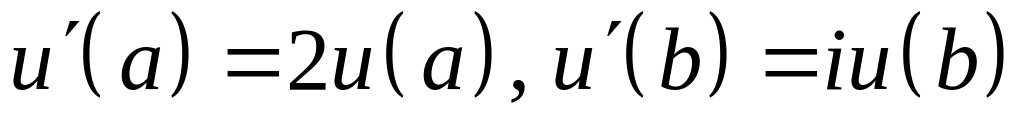 ;
;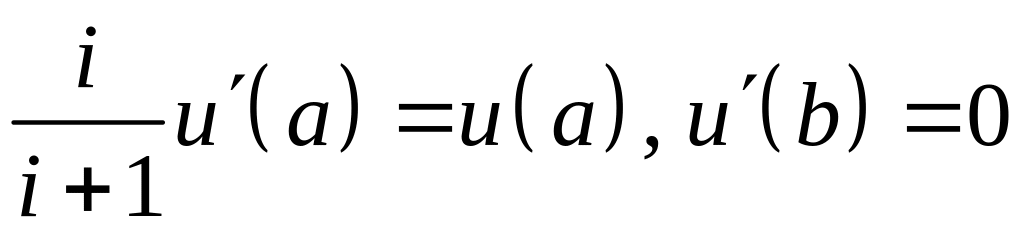 ;
;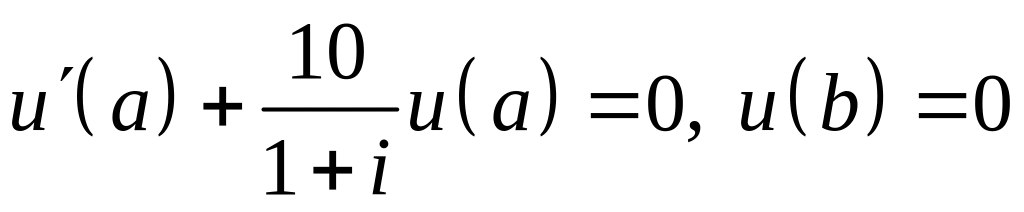 ;
;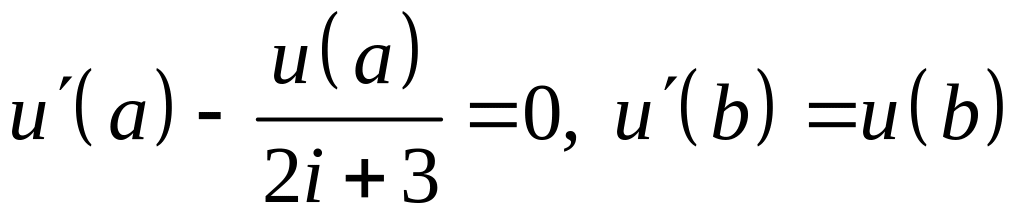 ;
;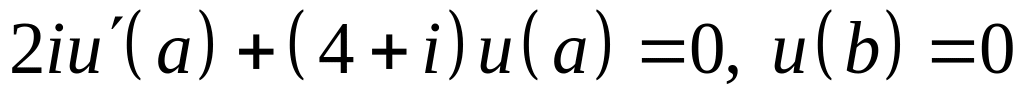 ;
; ;
; ;
; ;
;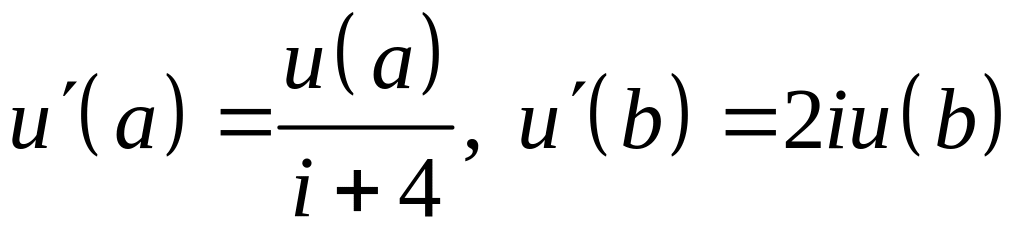 .
.
Типовой расчет № 2 «Интегральные уравнения»
I.
Для заданного ядра
![]() интегрального оператора, заданного на
отрезке
интегрального оператора, заданного на
отрезке
![]()
1) построить резольвенту Фредгольма тремя способами:
а) с помощью ряда Неймана;
б) с помощью рядов Фредгольма;
в) как для вырожденного ядра.
2) найти характеристические значения и собственные функции двумя способами:
а) как для вырожденного ядра;
б) через особенности резольвенты Фредгольма.
1)
Пусть
![]() ,
,
![]() ,
,
![]() .
.
Речь идет о решении интегрального уравнения
![]() ,
(1)
,
(1)
где
![]() - интегральный оператор с ядром
:
- интегральный оператор с ядром
:
![]() ,
(2)
,
(2)
![]() -
заданная функция.
-
заданная функция.
а) Решение уравнения (1) будем искать методом последовательных приближений. Для этого полагаем
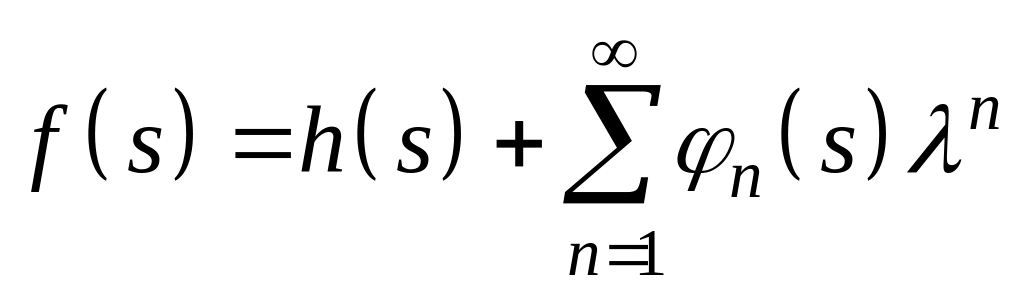 ,
,
где
функции
![]() задаются формулами:
задаются формулами:
![]() ,
,
![]() для
для
![]() ,
,
где
![]() называется итерированным ядром и
определяется как
называется итерированным ядром и
определяется как
![]() , (3)
, (3)
![]() .
.
Тогда
решение уравнения (1) может быть найдено
в виде
![]() ,
где
,
где
![]() - интегральный оператор с ядром
- интегральный оператор с ядром
![]() ,
называемым резольвентой Фредгольма.
Для резольвенты Фредгольма справедливо
равенство
,
называемым резольвентой Фредгольма.
Для резольвенты Фредгольма справедливо
равенство
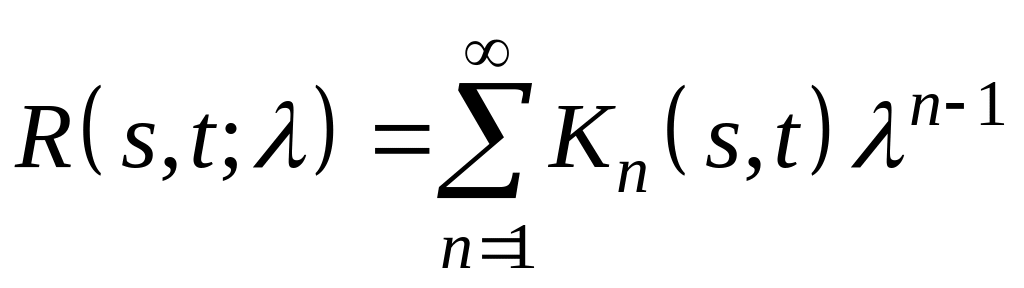 ,
(4)
,
(4)
где ряд, стоящий справа, называется рядом Неймана.
Найдем последовательно итерированные ядра, следуя формуле (3). Имеем
![]() ,
,
![]() ,
,
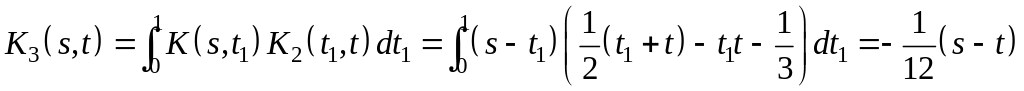 ,
,
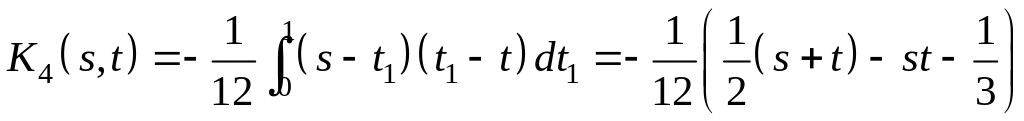 ,
,
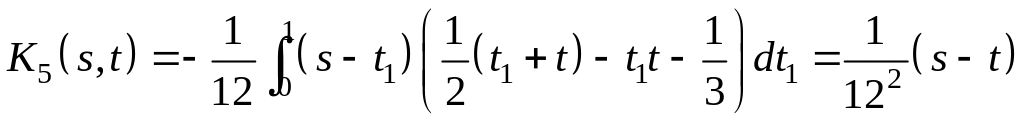 .
.
Методом математической индукции можно доказать, что итерированные ядра имеют вид:
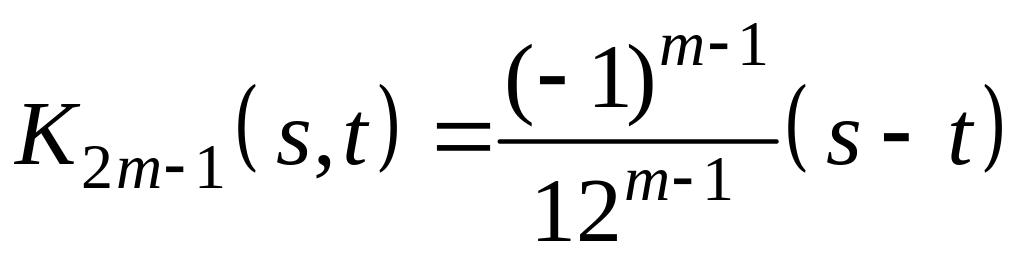 ,
,
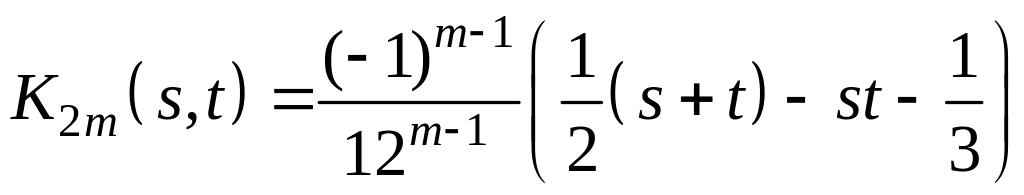 ,
,
где
![]() .
.
Тогда ряд Неймана для резольвенты примет вид
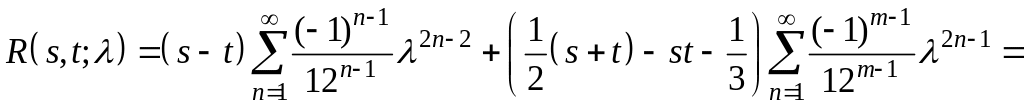
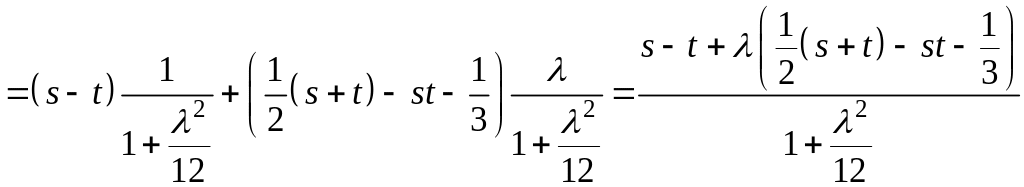 .
.
б) Резольвента Фредгольма уравнения (1) может быть найдена по формуле:
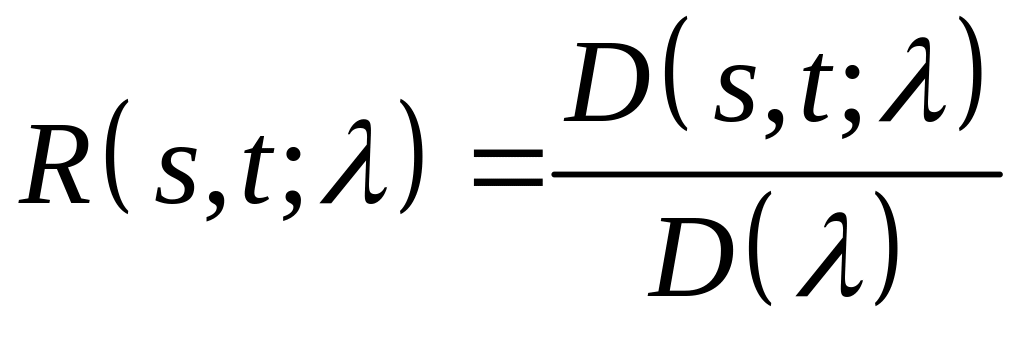 ,
,
где
функции
![]() и
и
![]() находятся с помощью рядов Фредгольма:
находятся с помощью рядов Фредгольма:
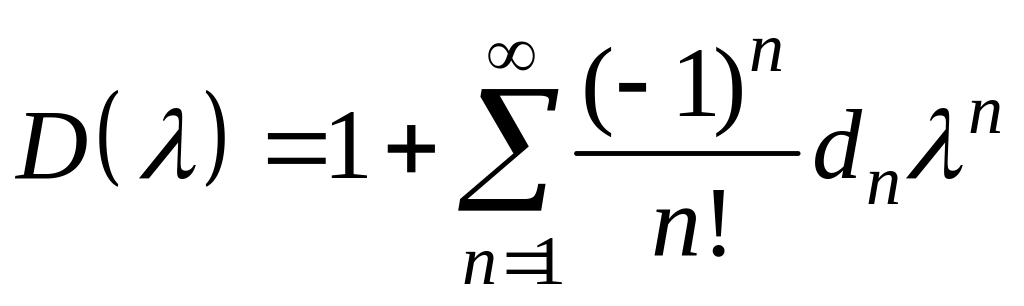 ,
,
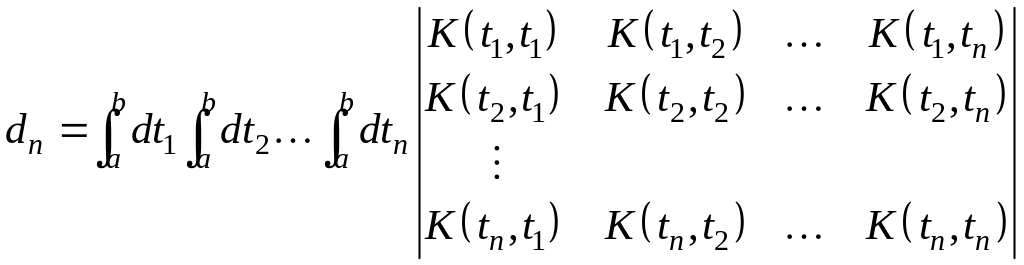 ,
,
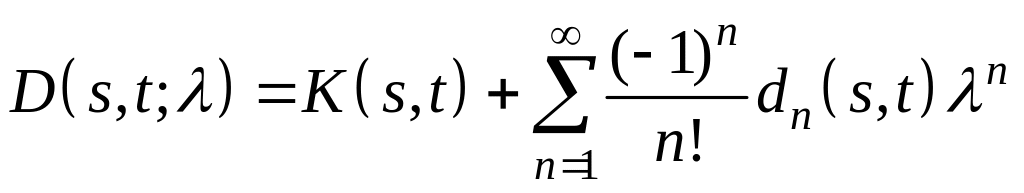 ,
,
 .
.
Имеем
![]() ,
,
 ,
,
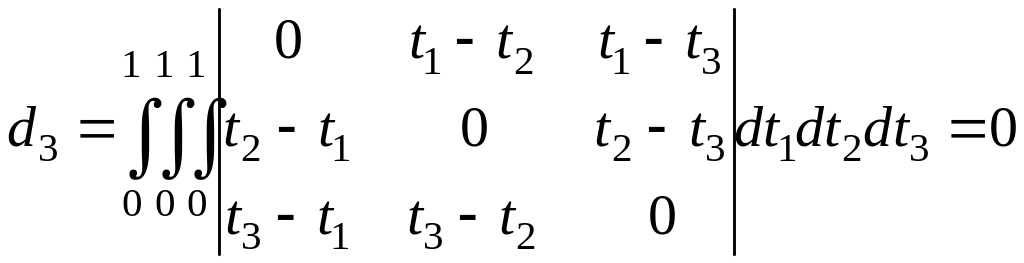 ,
,
так
как подынтегральный определитель равен
нулю. Очевидно, что
![]() при
при
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Далее,
 ,
,
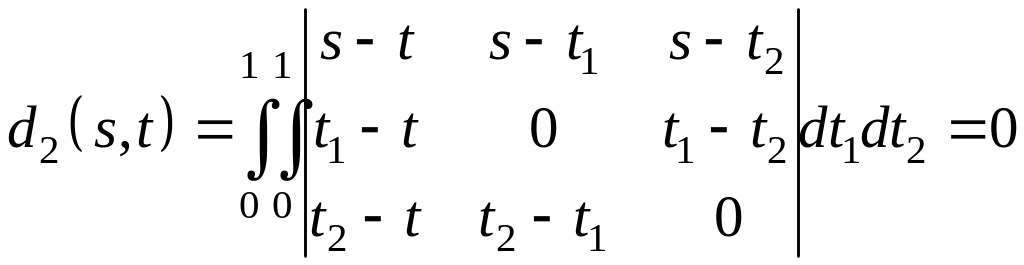 ,
,
так
как подынтегральный определитель равен
нулю. Очевидно, что
![]() при
.
Следовательно,
при
.
Следовательно,
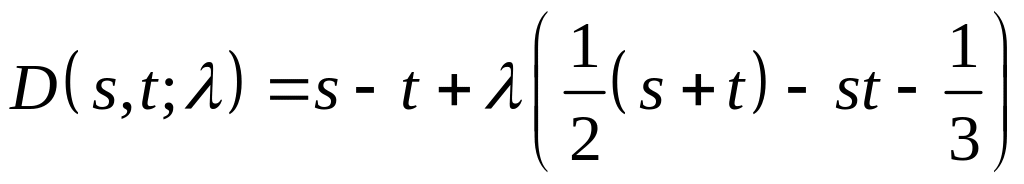 .
.
Окончательно, получаем резольвенту
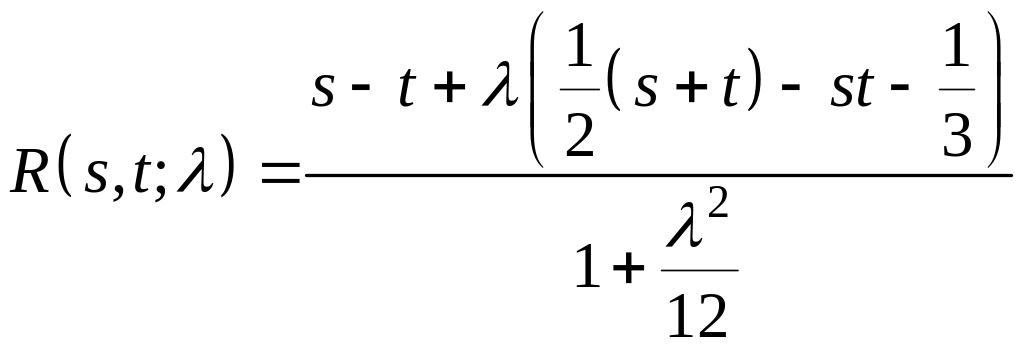 .
.
в) Перепишем уравнение (1) в виде
![]() .
.
Введем обозначения
![]() ,
,
![]() .
(5)
.
(5)
Тогда уравнение (1) равносильно равенству
![]() .
(6)
.
(6)
Подставим
выражение (6) в равенства (5). Получим
систему уравнений для
![]() и
и
![]() :
:
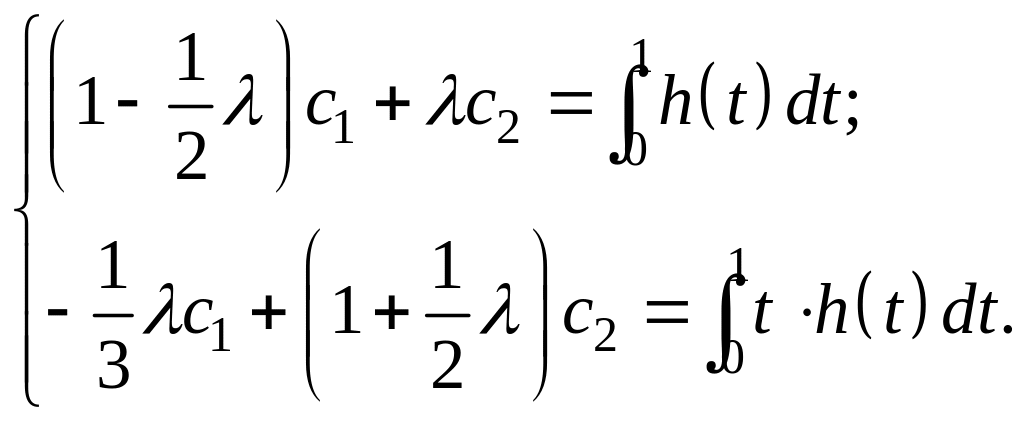
Решение этой системы имеет вид
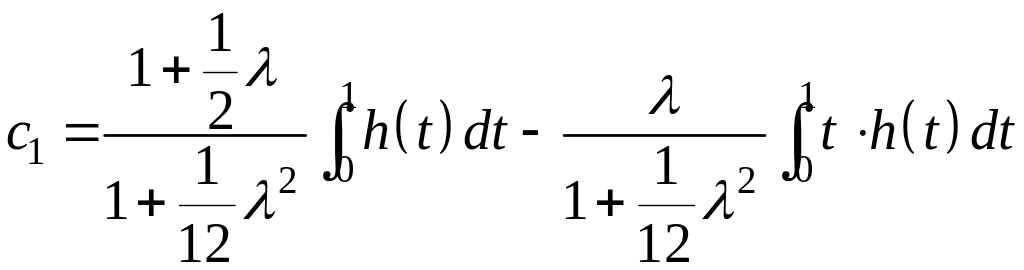 ,
,
 .
.
Далее, записывая решение (6) уравнения (1), получаем резольвенту Фредгольма
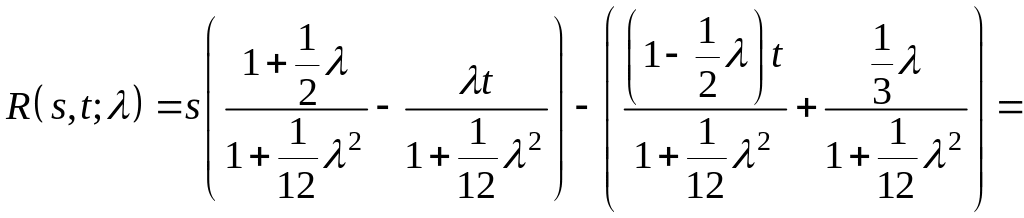
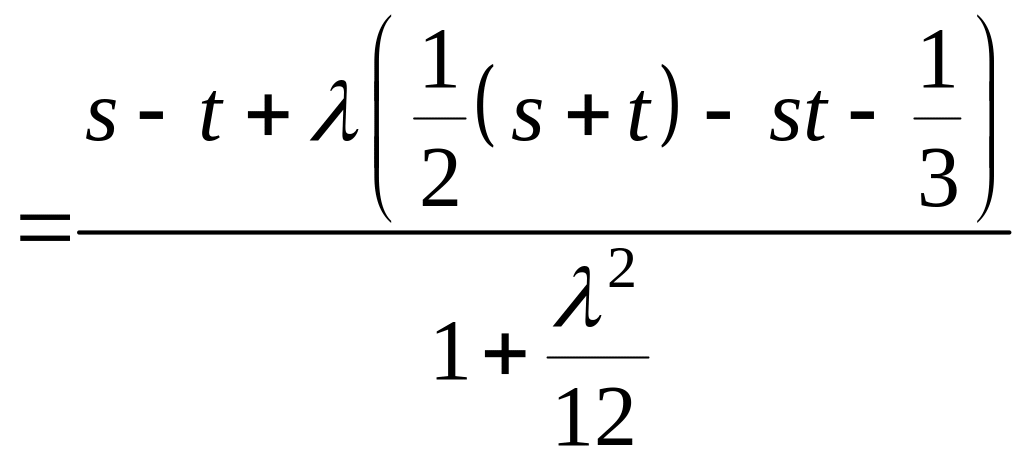 .
.
2)
Пусть
![]() ,
,
.
,
,
.
а) Запишем однородное уравнение Фредгольма в виде
![]() .
.
Вводя обозначения
, ,
получим
![]() .
.
Тогда для и имеем систему уравнений:
 (7)
(7)
Из условия существования нетривиального решения

находим
характеристические значения
![]() .
.
Так
как из (7) следует, что
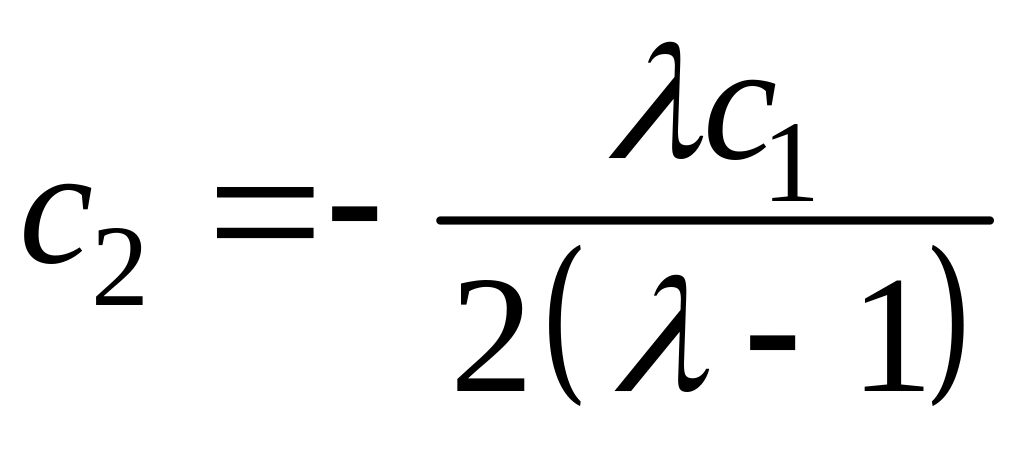 ,
то подставляя
,
то подставляя
![]() ,
получаем выражения для собственных
функций:
,
получаем выражения для собственных
функций:
![]() ,
,
где
![]() .
.
б)
Известно, что характеристические числа
интегрального уравнения являются
полюсами резольвенты
(как функции от
![]() ),
а ее коэффициенты рядов Лорана (в
выколотых окрестностях этих полюсов)
при наибольшей по модулю отрицательной
степени дают соответствующие этим
значениям собственные функции (как
функции от первого аргумента при любом
значении
),
а ее коэффициенты рядов Лорана (в
выколотых окрестностях этих полюсов)
при наибольшей по модулю отрицательной
степени дают соответствующие этим
значениям собственные функции (как
функции от первого аргумента при любом
значении
![]() ).
).
Пусть для ядра , , резольвента уже найдена:
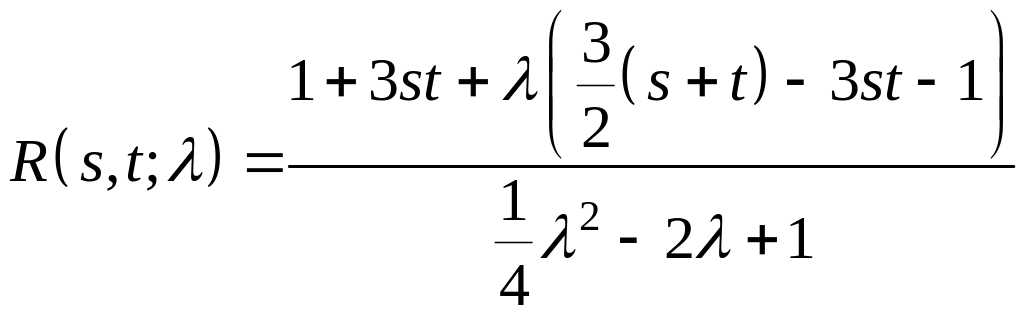 .
.
Числа - ее простые полюса. Имеем для собственной функции
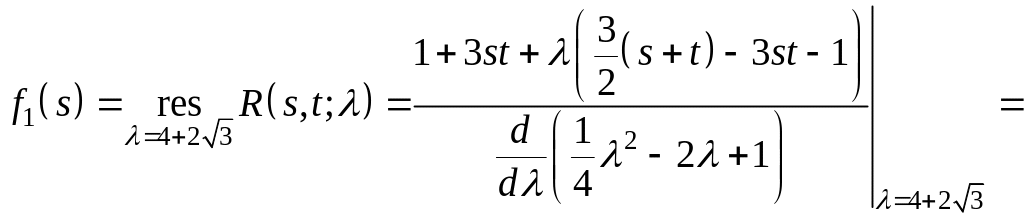
![]() ,
,
где
![]() .
.
Аналогично
находится
![]() .
.
II. Решить уравнение или систему уравнений.
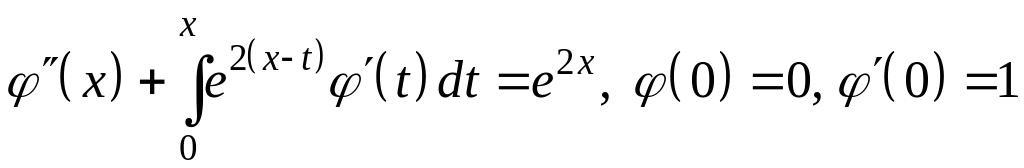 .
.
Применим
преобразование Лапласа к левой и правой
частям. Обозначим образ функции
![]() .
Имеем для правой части
.
Имеем для правой части
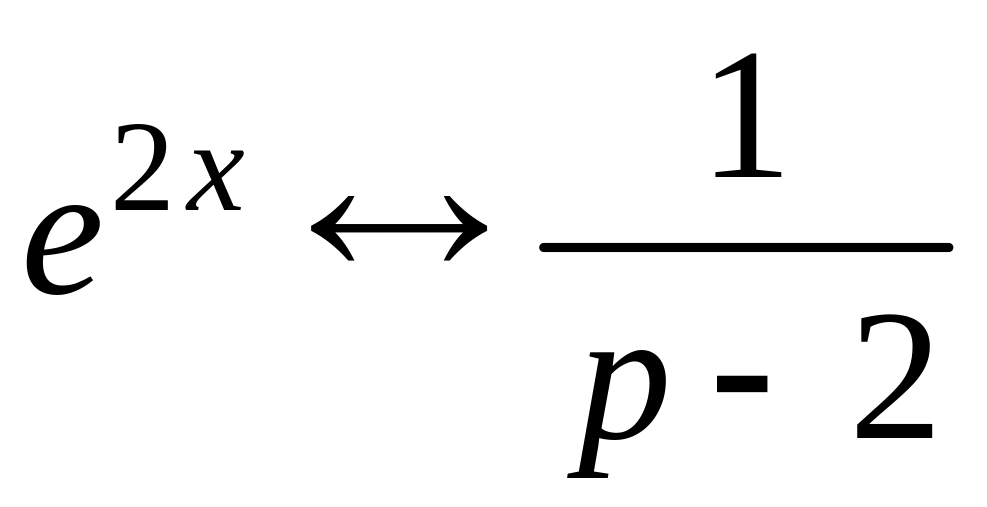 .
.
В силу правила дифференцирования оригинала и учитывая данные начальные условия, получим
![]() ,
,
![]() .
.
Пользуясь свойством умножения изображений, получим
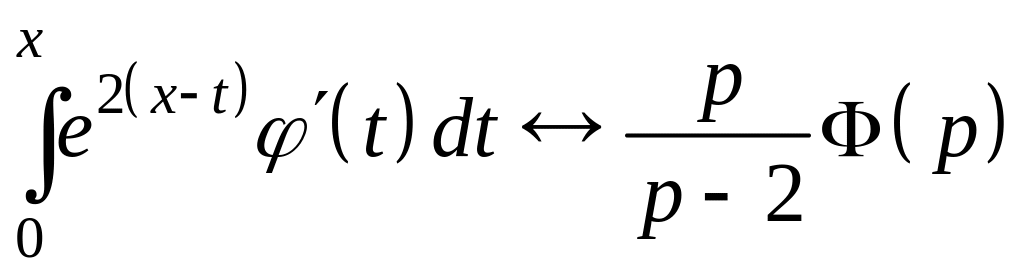 .
.
Тогда уравнение для образа искомой функции примет вид
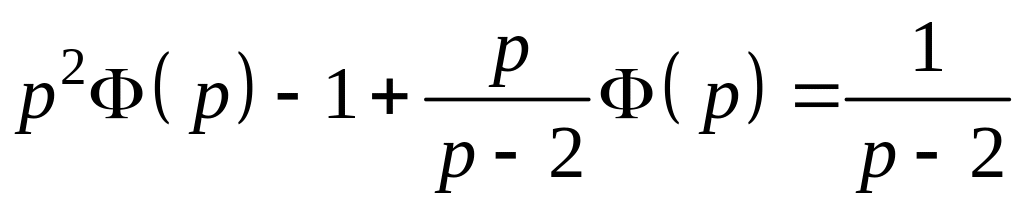 .
.
Решая
его, получим
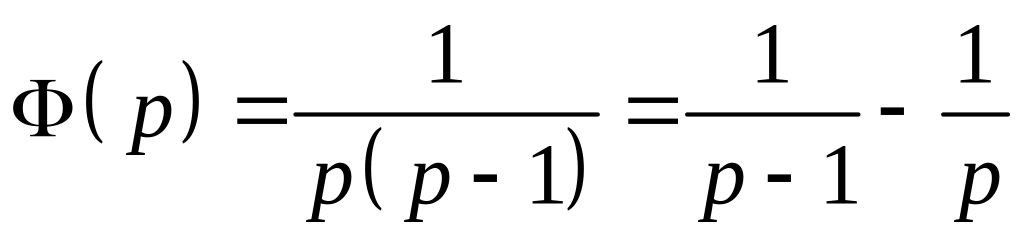 .
Следовательно, решение исходного
уравнения с данными начальными условиями
имеет вид
.
Следовательно, решение исходного
уравнения с данными начальными условиями
имеет вид
![]() .
.
