4.3. Метод векторных диаграмм

4.3.1. Метод векторных диаграмм дает возможность заменить ал­гебраическое сложение синусоидальных величин геометрическими дей­ствиями над векторами в соответствии с правилами векторного анализа.

4.3.2. Метод векторных диаграмм состоит в следующем:

каждой синусоидальной величине соответствует вектор этой вели­чины;

направление вектора синусоидальной величины определяется началь­ной фазой;

модуль вектора синусоидальной величины пропорционален действу­ющему значению или амплитуде этой величины;

векторы синусоидальных величин одинаковой угловой частоты мож­но складывать геометрически как обычные векторы.

Положительное направление угла отсчитывается против хода часовой стрелки.

4.3.3. Таким образом, если нужно опреде­лить ток

то в соответствии с первым законом Кирхго­фа (рис. 4.1) можно провести такие алгебраи­ческие действия:

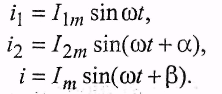
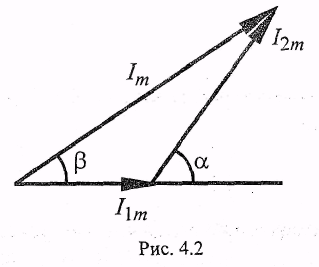Амплитуду и начальную фазу тока определить очень трудно. Согласно методу векторных диаграмм этот ток проще определить с помощью вектор­ной диаграммы, которая обязательно строится в масштабе (рис. 4.2).

4.4. Символический метод

4.4.1. Для расчета цепей синусоидального тока применяется также символический метод.

Символический метод дает возможность заменить геометрические действия над векторами алгебраическими. При этом расчеты цепей переменного тока проводят таким же способом, что и цепей постоянно­го тока.

4.4.2. Символический метод состоит в следующем:

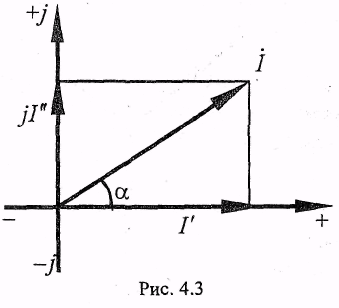
а) каждый вектор I раскладывается на составляющие и на осях прямоугольной системы координат (рис. 4.3);

б) ось абсцисс называют осью действительных значений и обознача­ют знаками «+» и «-». Ось ординат называют осью мнимых значений. Составляющую вектора на мнимой оси выделяют особым символом j. По­этому данный метод называется символическим. Вектор

в) умножение каждого вектора на символу поворачивает этот вектор на 90° против хода часовой стрелки. Умножение на поворачивает вектор на 180°, т.е.

отсюда Символ — это мнимая единица;

г) вектор рассматривается как величина комплексная на комплекс­ной плоскости. Поэтому данный метод также называется «методом ком­плексных величин».

4.4.3. Действующие значения в комплексной форме записывают ос­новным буквенным обозначением, над которым ставят точку. Применя­ются три формы записи комплексных величин:

а) алгебраическая форма

б) тригонометрическая форма

в) показательная форма

Последнее вытекает из формулы Эйлера

Для перехода от одной формы к другой используются соотношения

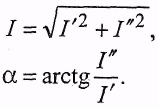
где — модуль комплекса; — начальная фаза.

4.5. Активное сопротивление в цепи синусоидального тока

4.5.1. Если на синусоидальное напряжение

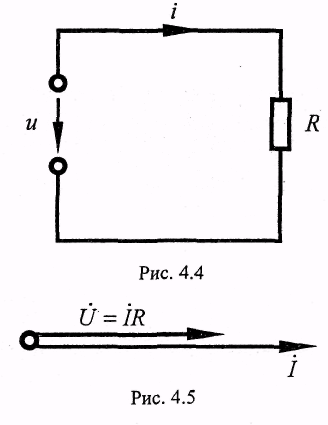
включить резистивный элемент (рис. 4.4), то в цепи возникнет мгно­венный ток

4.5.2. Таким образом, можно сделать вывод, что ток в цепи с активным со­противлением, включенным на сину­соидальное напряжение, является синусоидальным и совпадает с напря­жением по фазе.

4.5.3. Векторная диаграмма такой цепи изображена на рис. 4.5.

Вектор тока совпадает по направле­нию с вектором напряжения (сдвиг по фазе равен нулю).

4.5.4. Закон Ома для такой цепи, в ам­плитудных значениях, действующих значениях и в комплексной форме имеет вид

4.5.5. Необходимо учитывать увеличение сопротивления проводни­ков переменного тока, связанное с явлением вытеснения тока на поверх­ность проводника. Поверхностный эффект учитывается введением ко­эффициента

где — сопротивление проводника постоянному току;

— сопротивление этого же проводника переменному току.