2.2. Смешанное соединение приемников

2.2.1. Часто электрическая цепь представляет собой смешанное соединение приемников (т. е. последовательное и параллельное соедине­ния резисторов).

Если цепь имеет только последовательное соединение сопротивлений (рис. 2.6), то эквивалентное сопротивление

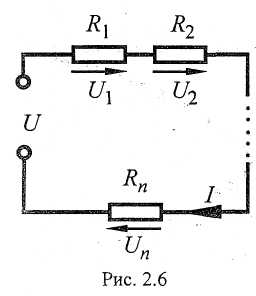Электрические величины определяют по та­ким соотношениям:

— ток в цепи,

— напряжение на элементе.

Мощность, которая выделяется на элементе,

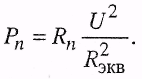
2.2.2. При параллельном соединении приемников (рис. 2.7)

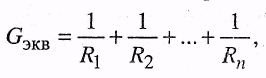
или

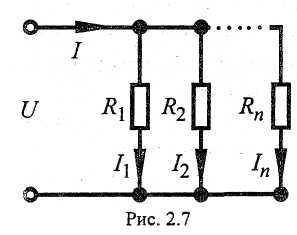и ли

Если цепь имеет лишь три приемника,

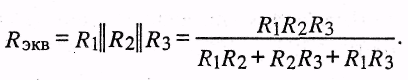
Если цепь имеет только два приемника,

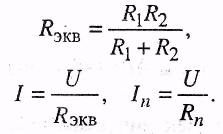
2.3. Применение законов Кирхгофа

2.3.1. Первый закон Кирхгофа

Алгебраическая сумма токов узла электрической цепи равна нулю

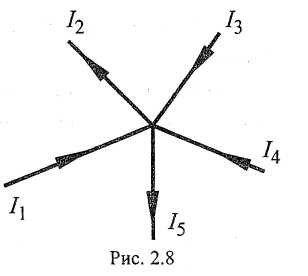
Для узла, приведенного на рис. 2.8,

2.3.2. Второй закон Кирхгофа

Алгебраическая сумма ЭДС любого замкнутого контура равна алгебраической сумме напряжений на элементах этого контура

Для цепи, приведенной на рис. 2.9,

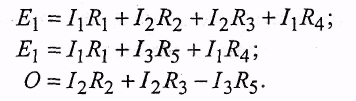
2.3.3. Чтобы рассчитать электрическую цепь с помощью законов Кирхгофа, нужно:

а) в цепи произвольно назначить направления тока;

б) составить уравнения по первому закону Кирхгофа на одно меньше, чем число узлов в цепи;

в) уравнения, которых недостает до полной системы, составить по второму закону Кирхгофа. Контуры нужно выбирать таким образом, чтобы в каждом была хотя бы одна ветвь, которая не рассматривалась ранее;

г) после определения токов нужно уточнить действительное направление этих токов.

2.3.4. Пример. Для расчета электрической цепи, приведенной на рис. 2.9, можно составить такие уравнения:

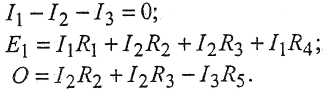
2.3.5. Из закона сохранения энергии вытекает понятие баланса мощностей.

Мощность всех источников питания электрической цепи равна сумме мощностей всех приемников этой цепи

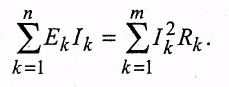
Если направления ЭДС и тока совпадают, то источник отдает мощность нагрузке. В этом случае произведение E_k I_k нужно брать со знаком «+». Если направления ЭДС и тока противоположные, то источник работает в режиме приемника (например, режим зарядки аккумулятора). В таком случае произведение нужно брать со знаком «-».

К мощности приемников нужно относить и мощность, которая выделяется на внутреннем сопротивлении источника питания.

2.4. Метод суперпозиции

2.4.1. Если цепь имеет несколько источников питания, то для расчета этих цепей можно применить метод суперпозиции (метод наложения). Этот метод использует принцип независимости действия ЭДС. Токи, которые создаются несколькими ЭДС, являются алгебраической суммой токов, создаваемых каждым источником в отдельности. Метод суперпозиции дает возможность заменить вычисление сложных цепей расчетами элементарных цепей с одним источником питания в каждой.

2.4.2. Вычисление сложных цепей с несколькими источниками питания по методу суперпозиции можно осуществить следующим образом:

а) сложную цепь заменяют несколькими цепями; каждая из которых имеет один источник в элементарной цепи, другие заменяют сопротивлениями, которые равны внутренним сопротивлениям источников;

б) рассчитывают элементарные цепи, определяя величины и направления токов в каждой ветви;

в) в каждой ветви находят действительные токи как алгебраическую сумму соответствующих токов, т. е. слагаемыми действительного тока являются токи этой ветви в элементарных цепях.

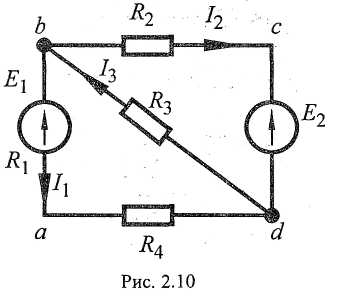Для примера можно вычислить цепь, приведенную на рис. 2.10. В первом случае рассмотрим цепь без ЭДС Е₂.

Внутреннее сопротивление этой ЭДС равно нулю. Все токи будем помечать штрихом, т. е.

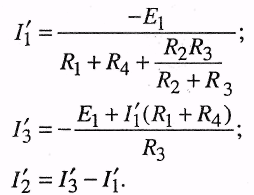
Дальше можно рассмотреть цепь без источника E₁, но учесть его внутреннее сопротивление R₁. Токи будем помечать двумя штрихами:

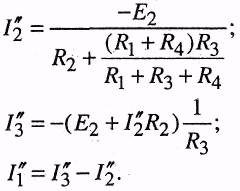
Действительные токи являются суммой соответствующих токов эле­ментарных цепей, т. е.: