Введение в численные методы

Обработка экспериментальных данных на компьютере

Обработка данных с использованием вычислительной техники является важнейшей отраслью современных информационных технологий. Для реализации задач обработки данных привлекаются разнообразные методы вычислительной математики. В данном разделе мы остановимся только на двух из таких методов – анализ корреляционных связей между двумя процессами и регрессионный анализ данных.

Прежде всего, необходимо отчетливо представлять, что любые экспериментальные данные, полученные в процессе измерений, содержат, наряду с некоторыми детерминированными функциональными связями, различного рода ошибки. Так, например, давление и температура при постоянном объеме связаны между собой прямой пропорциональной зависимость. Как это следует из универсального газового закона. Однако, во-первых, сам этот закон представляет собой некоторую идеализацию, и, во-вторых, экспериментальная проверка этого закона всегда будет содержать инструментальные ошибки так, что линейная зависимость будет наблюдаться лишь приближенно. Возникает вопрос: как количественно оценить эту самую степень приближенности. Ответ на этот вопрос как раз и дает корреляционный анализ. Итак, речь идет не об установлении строгой функциональной зависимости - в реальном эксперименте такая детерминированная зависимость скорее исключение, а не правило. Мы говорим о статистической связи – связи в среднем.

Для количественного описания статистической связи между двумя величинами вводят КОЭФФИЦИЕНТ ПАРНЫХ КОРРЕЛЯЦИЙ, который также известен как уоэффициент корреляции Пирсона. Если измерены два набора значений величин x_i, y_i, что наиболее наглядно можно представить как значения, измеренные в различные моменты времени t₁, t₂, ... t_N, то коэффициент корреляции между ними определяется по формуле:

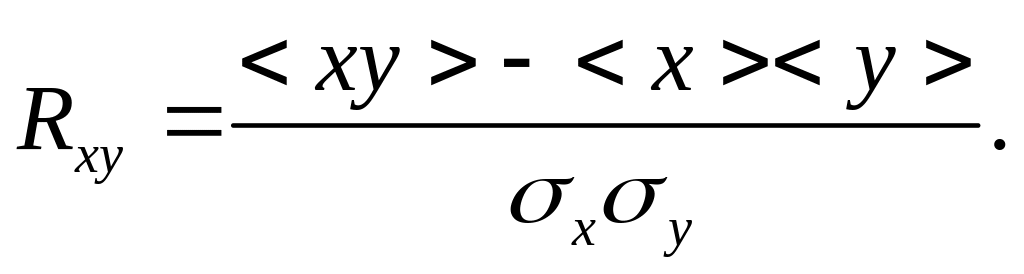
Здесь угловые скобки < > означают усреднение, а _x, _y есть среднеквадратичные отклонения соответствующих величин.

Конкретно, в нашем случае, коэффициент корреляции рассчитывается следующим образом:

Эта формула построена так, что коэффициент корреляции может принимать значения в интервале [-1,+1]. При этом значения +1 и –1 достигаются только, если x и y связаны строго линейной зависимостью y=ax+b. Знак R, при этом, соответствует знаку коэффициента a. Таким образом, коэффициент парных корреляций является мерой близости статистической связи двух переменных величин к линейной зависимости. Если величина R близка по абсолютной величине к единице, то имеет место сильная корреляционная связь между величинами, а, если она мала по сравнению с 1, то измеренные величины можно считать независимыми.

Можно предложить несколько вариантов моделирования корреляционных связей между двумя процессами, наглядно иллюстрирующих методику применения коэффициента парных корреляций.

1. Если две последовательности сформировать как массивы данных, вырабатываемых генератором случайных чисел с нулевым средним, то коэффициент корреляции для таких последовательностей должен быть весьма малой величиной по сравнению с единицей. Если в процессе моделирования окажется, что это не так, то, скорее всего, вы имеете недостаточно хороший генератор случайных чисел.

2. Если задать произвольную последовательность чисел х, и из нее образовать последовательность y путем любого линейного преобразования первой, то коэффициент корреляции должен быть равным +1 или -1. Если это не так, то вы ошиблись в построении программы вычислений.

Вторая процедура, широко применяемая при обработке экспериментальных данных, позволяет наилучшим способом аппроксимировать взаимосвязь двух физических величин той или иной функциональной зависимостью. Речь идет о так называемом РЕГРЕССИОННОМ АНАЛИЗЕ данных. Считается, что предполагаемый характер связи двух величин x и y известен. Это может быть линейная, квадратичная зависимости, экспоненциальная связь или что-либо иное. Задачей регрессионного анализа является определение коэффициентов или параметров выбранной функциональной зависимости, при которых аппроксимирующая функция наиболее точно отображает наблюдаемые значения.

Допустим, предполагается, что величины x и y связаны между собой линейной зависимостью. В этом случае мы говорим о линейном регрессионном анализе. В плоскости XOY можно построить "облако" точек с координатами x_i, y_i, i=1,2,...N, полученных в результате измерений, как это показано на рисунке.

Нашей задачей является выбор коэффициентов a и b функциональной зависимости y=ax+b, при которых соответствующая прямая проходит через "облако" точек наилучшим образом. Для того чтобы конкретизировать это самое понятие "наилучшим образом" прибегнем к МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ. В общем случае аппроксимирующую зависимость y=f(x;a,b,c,...) будем рассматривать как функцию от параметров a,b,c,... Величину y_i-f(x_i;a,b,c,...) называют невязкой для i - й экспериментальной точки. Она показывает, насколько данная точка не укладывается в выбранную аппроксимирующую зависимость. Очевидно, что невязка может быть как положительной, так и отрицательной. В частности, на предыдущем рисунке невязка для выбранной точки показана вертикальным отрезком, соединяющим точку с аппроксимирующей прямой, и здесь она положительна.

В основу метода наименьших квадратов положено требование минимальности суммы квадратов невязок:

Фигурируют именно квадраты, поскольку невязки могут иметь разные знаки. Величину J можно рассматривать как функцию параметров a,b,c,.... Тогда условие минимальности функционала невязок будет представлять собой систему уравнений:

Для линейной регрессии будем иметь:

Имеем систему двух линейных алгебраических уравнений с двумя неизвестными, решение которой дает расчетные формулы линейного регрессионного анализа:

При использовании более сложной, по сравнению с линейной, регрессии, задача определения параметров несколько усложняется, но принципиальных трудностей и здесь не возникает.

Решение трансцендентных уравнений

В данном разделе речь идет о численных методах решения уравнения f(x)=0 в области действительных чисел. В общем случае функция f(x) может быть совершенно произвольной, в отличие, например, от линейной или степенной, то есть алгебраической. В математике в этом общем случае говорят о так называемых трансцендентных уравнениях. В общем виде задача может быть сформулирована следующим образом. Необходимо найти такое значение x₁, которое приближенно совпадает со значением x₀, обращающим уравнение в тождество. Требуется, однако, существенно дополнить постановку задачи. Во-первых, поскольку уравнение может и не иметь решения, следует быть уверенным в том, что поставленная задача имеет смысл - нельзя поймать черную кошку в темной комнате, если ее там нет. Во-вторых, поскольку уравнение может иметь несколько корней, необходимо ограничить интервал поиска корня отрезком [a,b], для которого известно, что на нем имеется только один корень. Признаком этого является то, что f(a) и f(b) имеют разные знаки. Термин "приближенно совпадает" также требует пояснения. Все приближенные методы нахождения корня строятся на основе итераций, когда очередное значение так или иначе получается из предыдущего и все ближе подходит к точному значению корня. Теперь можно сформулировать условие прекращения этого итерационного процесса. Процесс поиска корня следует прекратить тогда, когда относительная разность двух последовательных приближений станет по абсолютной величине меньше заданной точности. Если максимальная допустимая ошибка задана величиной , а два последовательных приближения являются значениями x_n-1 и x_n, то условие прекращения итераций примет вид:

.

Неприятность может произойти, если корнем уравнения является 0, однако это уже совсем особый случай, который рассматриваться не будет.

Наиболее наглядным, простым в реализации, однако, увы, не самым лучшим численным методом поиска корней, является МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ. Суть метода проще всего проиллюстрировать графически, с помощью следующего рисунка.

Прежде всего, находится точка , делящая отрезок [a,b], на котором ищется корень, пополам. Еще раз напомним, что корень на этом отрезке обязан быть. Далее, из этих двух половин выбирается та, на концах которой функция имеет разные знаки, то есть та, на которой имеется корень. Если эта половина является отрезком [c,b], как на нашем рисунке, то новым левым концом отрезка становится точка с. В противном случае точка с становится новым правым концом отрезка. Таким образом, после каждого такого выбора мы имеем новый отрезок [a,b], к которому снова применяем половинное деление. В этом методе наиболее наглядно выглядит условие выхода из цикла . А почему мы здесь обошлись без знака абсолютного значения? Автор надеется, что читатель сможет дать ответ на этот вопрос самостоятельно.

Более быстродействующим, по сравнению с методом половинного деления, является способ поиска корня, названный МЕТОДОМ ХОРД. Графическая иллюстрация метода представлена на рисунке, приведенном ниже. Для построения алгоритма метода хорд необходима дополнительная информация о характере поведения функции на интервале поиска корня. Прежде всего, необходимо гарантировать, что на этом интервале функция монотонна (монотонно возрастает или монотонно убывает). Кроме того, на всем интервале не должен меняться характер выпуклости или вогнутости. Иными словами, на [a,b] не должны менять знак ни первая, ни вторая производные функции. Вообще говоря, даже и при нарушении этих условий метод хорд можно применять, но с использованием специальных приемов, на которых мы не будем останавливаться. Проще всего в сомнительных случаях просто сузить интервал до такого размера, на котором производные знак не меняют.

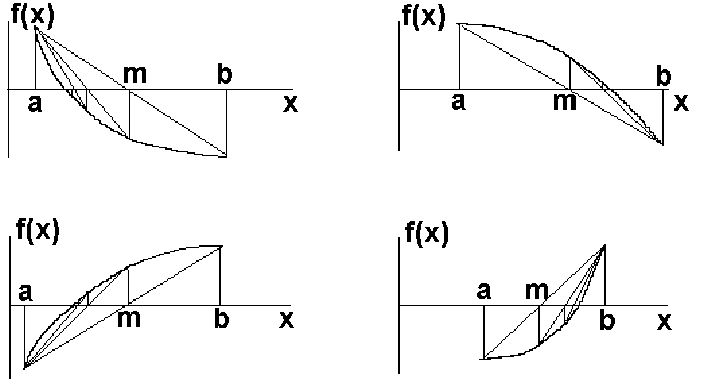
Из геометрии рисунка (подобия треугольников) можно найти точку m пересечения хорды с осью абсцисс. Поскольку , то . Дальнейшее построение алгоритма зависит от соотношения знаков первой и второй производных. Если знаки производных различны - левая часть рисунка, то новым правым концом интервала поиска корня становится точка m, то есть делается замена b на m. В противном случае, соответствующем двум вариантам правой части рисунка, делается замена a на m. Итерационный процесс продолжается до достижения необходимой точности.

Метод хорд действительно значительно более оперативен по отношению к методу деления отрезка пополам. В этом можно убедиться, реализовав оба метода для нахождения корня одного и того же уравнения на одном и том же отрезке и при одной и той же точности. Следует, однако, заметить, что выигрыш во времени будет иметь место только при оптимально написанной программе. В первую очередь, необходимо сократить до минимума количество вызовов функции f(x). Так в приведенном выше выражении для величины m по два раза фигурируют функции f(a) и f(b). Разумеется, функцию необходимо посчитать один раз, запомнить ее значение в какой-либо переменной и во второй раз использовать уже не вызов функции, а эту переменную.

Рассмотренные методы не исчерпывают арсенала средств поиска корней уравнений. Существуют методы более оптимальные либо по времени, либо по расходованию памяти компьютера. Кроме того, имеются методики, оптимальные для конкретных видов функций, для которых решается уравнение. Так, например, существуют алгоритмы, позволяющие находить группы корней, если функция является алгебраическим полиномом (причем корни могут быть найдены в комплексной области). Алгоритмы эти выглядят, однако, довольно сложными и не могут быть рассмотрены здесь.

Вычисление определенных интегралов

Необходимость в вычислении определенных интегралов с использованием численных методов возникает, в основном, в двух случаях. Во-первых, подынтегральная функция может быть задана таблично, например, как полученная в результате каких-либо измерений. Во-вторых, первообразная не может быть найдена в аналитическом виде, то есть, интеграл не является табличным. Как и все вычислительные методы, численное интегрирование является приближенным, и интеграл может быть получен с заданной точностью.

Простейшим методом численного интегрирования является МЕТОД ТРАПЕЦИЙ. Речь идет о вычислении интеграла . Метод применим, если пределы интегрирования конечны, а подынтегральная функция не имеет особенностей, хотя несложная предварительная процедура деления интервала интегрирования на несколько частей позволяет применить эту методику и к интегрированию функции, имеющей конечное число разрывов первого рода.

В методе трапеций интервал [a,b] разбивается на n элементарных отрезков длиной точками с координатой . На каждом из элементарных отрезков подынтегральная функция заменяется линейной функцией, а соответствующий участок площади под кривой y=f(x) заменяется трапецией так, как это показано на рисунке.

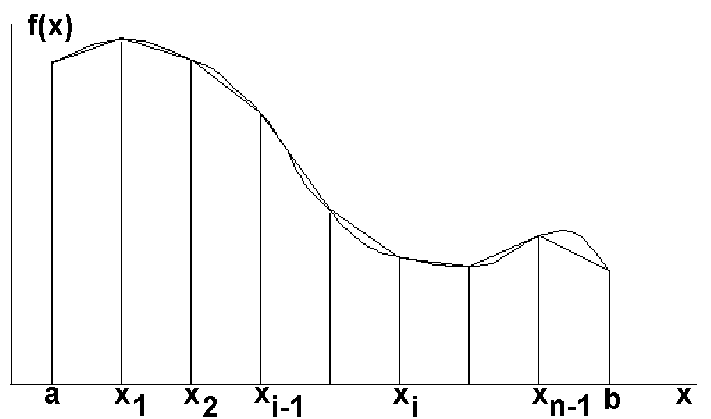
Исходя из известной формулы для площади трапеции, нетрудно получить выражение для приближенного значения интеграла:

Эту формулу наиболее удобно использовать, если интегрируется функция, заданная таблично, причем, координаты x_i могут быть расположены на интервале [a,b] произвольным образом (не обязательно равноудалены друг от друга).

Для вычисления интеграла от функции, заданной аналитически, целесообразно воспользоваться другим представлением формулы трапеций. В этом случае отрезок [a,b] может быть разбит на n равных отрезков длиной h. При этом предыдущая формула упрощается и принимает вид:

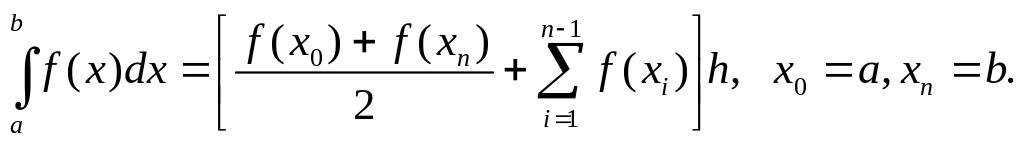
Здесь x_i=a+i*h.

Каким образом может быть достигнута заданная точность вычисления интеграла? Для функции, заданной таблично, возможности здесь весьма ограничены. Можно попытаться применить к подынтегральной функции какую-либо интерполяцию, приведя ее к функции, заданной аналитически, а затем применить описанную ниже итерационную процедуру. Однако, вряд ли на этом пути вы получите сколько-нибудь значимое улучшение точности. Для аналитически заданной подынтегральной функции желаемая точность может быть достигнута увеличением числа разбиений области интегрирования.

Метод трапеций наиболее прост, но не является оптимальным по быстродействию. Ненамного более громоздким, но значительно более оперативным является МЕТОД СИМПСОНА. Не вдаваясь в детали, укажем, что в этом методе отдельные участки подынтегральной функции представляются не линейной, как в методе трапеций, а квадратичной интерполяцией. По этой причине метод Симпсона имеет второе название - метод парабол. В этой методике число разбиений области интегрирования n должно быть четным. Тогда формула Симпсона запишется в виде:

В данном разделе было бы естественным представить методы вычисления кратных (двойных, тройных и так далее) определенных интегралов. Однако, мы отложим этот вопрос на будущее. Дело в том, что применение к кратным интегралам концепций методов трапеций или парабол сталкивается с рядом серьезных проблем. Так, для двойных интегралов, область интегрирования следовало бы разбивать на прямоугольные или квадратные малые подобласти. При этом возникает достаточно нетривиальная задача правильного учета произвольной формы границы. Еще большие проблемы связаны с аппроксимацией "вырезаемого" подобластью участка телом с достаточно просто вычисляемым объемом. Хотя указанные проблемы в принципе решаемы, более эффективным оказывается применение здесь одного из приложений общей концепции методики статистических испытаний или метода Монте-Карло. Рассмотрению этой концепции посвящен следующий раздел, где и описаны средства вычисления кратных интегралов.

Метод Монте – Карло

Вынесенный в заголовок данного раздела метод Монте-Карло на самом деле включает в себя чрезвычайно широкий набор средств решения разнообразных вычислительных задач и задач математического моделирования. По этой причине довольно затруднительно дать исчерпывающее определение этого метода. Мы и не будем стараться это делать, а попытаемся продемонстрировать суть метода на нескольких конкретных примерах. Часть этих примеров находится и в следующих главах книги.

Так или иначе, метод Монте-Карло, называемый иногда методом статистических испытаний, основан на имитации случайных событий и генерации случайных чисел и случайных функций. Применительно к моделированию сложных систем, метод подвергает систему испытаниям в различных возможных ситуациях, и на основе обработки данных о результатах большого числа таких испытаний делаются выводы о функционировании системы. При этом испытания проводятся не в натурных экспериментах, а, как теперь модно говорить, в виртуальном мире компьютера. Как мы увидим далее, метод Монте-Карло применяется и для чисто математических вычислительных задач.

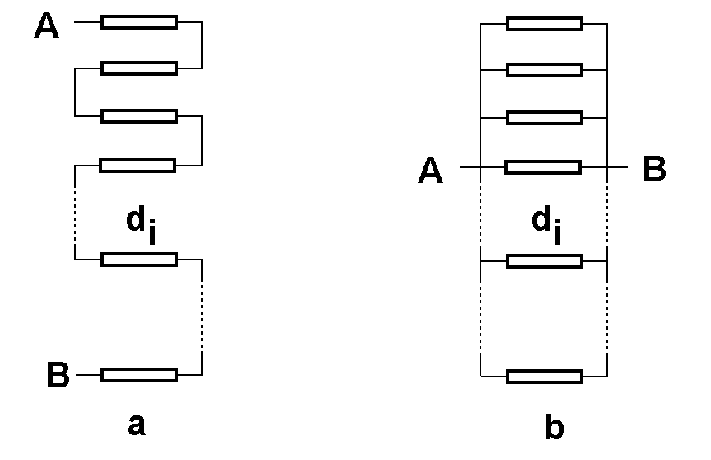
Первый пример, который мы рассмотрим, относится к задачам расчета надежности систем. Обратимся к приведенному выше рисунку. Допустим, назначение системы состоит в обеспечении возможности перехода из точки A в точку B. Каждый из элементов системы, обозначенный прямоугольником, может находиться в рабочем состоянии или в состоянии отказа. Состояние отказа заключается в том, что при этом переход по данному "мостику" невозможен. Коэффициент готовности i-го элемента, то есть вероятность того, что элемент находится в рабочем состоянии, задается величиной d_i. Очевидно, коэффициент отказа - вероятность того, что элемент находится в нерабочем состоянии, есть величина r_i=1-d_i. Мы рассматриваем два типа систем: последовательную - рисунок а и параллельную - рисунок b. Очевидно, отказ любого из элементов последовательной системы приведет к отказу всей системы - переход от точки A к точке B невозможен. Тогда коэффициент готовности всей системы есть произведение коэффициентов готовности всех элементов D_послед=d₁d₂...d_n, а коэффициент отказа системы есть R_послед=1-D_послед. Для параллельной системы картина, в каком-то смысле, противоположная. Система будет находиться в состоянии отказа только тогда, когда все элементы находятся в состоянии отказа. Коэффициент отказа системы в этом случае равен произведению коэффициентов отказа всех элементов R_парал=r₁r₂...r_n, а коэффициент готовности D_парал=1-R_парал.

То, что мы сейчас сделали, является, в чистом виде, математическим моделированием систем. Математический аппарат, примененный здесь, весьма прост. Использована теорема теории вероятностей, гласящая, что вероятность одновременной реализации нескольких независимых случайных событий равна произведению вероятностей реализации каждого из событий. Относительно простая структура моделируемых систем позволила обойтись без привлечения численных методов анализа. Кроме того, все, что только что обсуждалось, не имеет пока никакого отношения к методу Монте - Карло, хотя бы уже потому, что здесь не использованы датчики случайных чисел.

Переход к статистическим испытаниям становится необходимым при рассмотрении более сложных систем. На следующем рисунке показана система, которую нельзя рассматривать ни как последовательную, ни как параллельную.

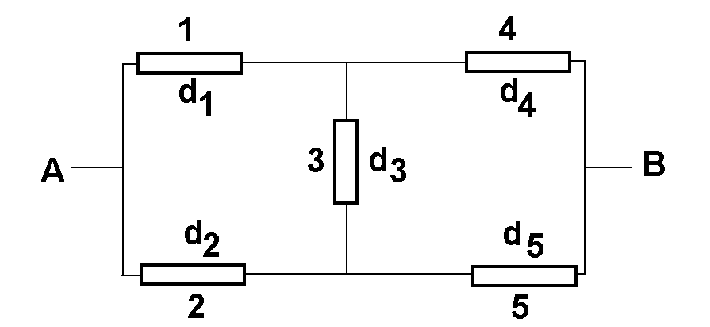
Откроем секрет - эта система все еще достаточно проста и может быть смоделирована без привлечения статистических испытаний. Но пора нам, наконец, заняться темой раздела. В данном случае метод Монте - Карло будет состоять в том, что каждый из элементов будет приводиться либо в рабочее состояние, либо в состояние отказа с вероятностями, заданными коэффициентами готовности d_i (разумеется, не в реальности, а в численном эксперименте). Для проведения массовых статистических испытаний понадобится генератор случайных, равномерно распределенных на интервале от 0 до 1, чисел. Для каждого i-го элемента определим индикаторную функцию I_i(s), принимающую значение 1, если s<=d_i и значение 0 в противном случае. Здесь s - генерируемое случайное число. В каждом отдельном испытании генерируется пятерка случайных чисел, и с их помощью формируется пятерка значений индикаторных чисел (пятерка нулей и единиц). Посмотрев на схему, можно убедиться, что система будет находиться в состоянии отказа, тогда и только тогда, когда реализуется один из следующих вариантов:

I₁+I₂=0,

I₄+I₅=0,

I₁+I₃+I₅=0,

I₂+I₃+I₄=0.

Анализ выполнения или невыполнения этих условий вполне можно поручить компьютеру. Проведя большое число испытаний, можно подсчитать процент случаев отказа, что и даст величину коэффициента отказа системы. Таким образом, мы имеем компьютерное моделирование системы, выполненное методом Монте - Карло. Это моделирование, действительно, компьютерное, поскольку компьютер выполняет две важнейшие функции - генерацию случайных чисел, анализ и подсчет работоспособности системы в каждой отдельной реализации испытаний.

Нам осталось только уточнить, что понимается под термином "большое число испытаний". Математики и здесь сказали свое слово. Относительная ошибка результата N статистических испытаний оценивается величиной . Что это значит? Это означает, что, если вы хотите получить в методе Монте - Карло результат с относительной ошибкой, не превышающей e, то надо провести не менее испытаний. Так, для достижений точности 0.01 (один процент) необходимо сделать не менее 5000 испытаний. Как видите, метод достаточно "накладен", но быстрое развитие вычислительной техники позволяет использовать его все в больших масштабах.

Итак, мы продемонстрировали применение метода статистических испытаний для моделирования работы систем. Теперь рассмотрим два примера использования этой методики в качестве численного метода.

Займемся приложением метода Монте - Карло к ВЫЧИСЛЕНИЮ КРАТНЫХ ИНТЕГРАЛОВ. Для того, чтобы слишком не усложнять себе жизнь, ограничимся случаем двойных интегралов. Переход к интегралам большей кратности не вызывает затруднений. Таким образом, речь идет о вычислении двойного интеграла:

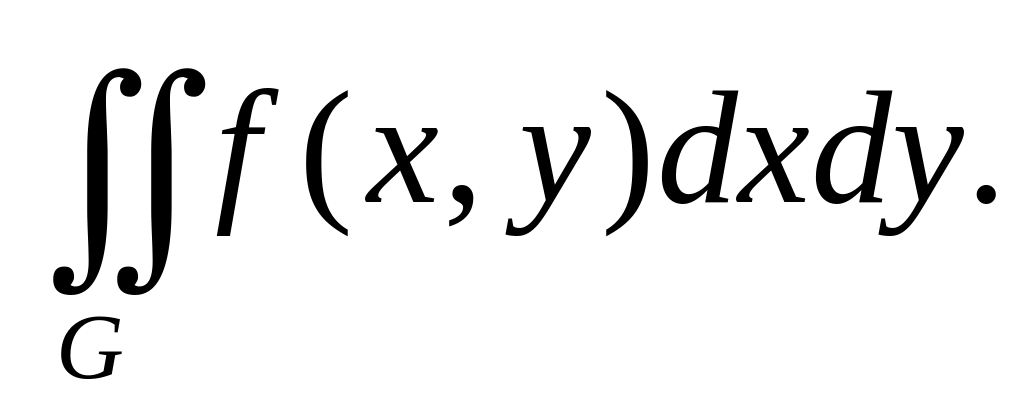
Если при интегрировании функции одной переменной, используется разбиение интервала интегрирования на малые отрезки, то в случае двойных интегралов необходимо разбивать на малые площадки двухмерную область интегрирования G. Если эта область является прямоугольником, то такое разбиение тривиально, но если область имеет произвольную форму, то задача разбиения становится очень непростой. Именно в этих условиях целесообразно использовать метод Монте - Карло. Обратимся к рисунку, иллюстрирующему геометрию задачи.

Поместим область интегрирования G целиком в прямоугольник, желательно с наименьшими размерами. С помощью генератора случайных вещественных чисел, равномерно распределенных на некотором интервале, "набросаем" в прямоугольник большое число N точек, координаты которых случайны. Для этого генератор должен многократно выдавать пары случайных значений, первое из которых (координата х) находится в интервале [a,b], а второе (координата y) - в интервале [c,d]. На каждую точку приходится малая удельная площадь . Теперь введем функцию F_i=F(x_i,y_i), которая для каждой i-ой точки принимает значение f(x_i,y_i), если точка принадлежит области G, и значение 0, если точка не попала в область интегрирования.

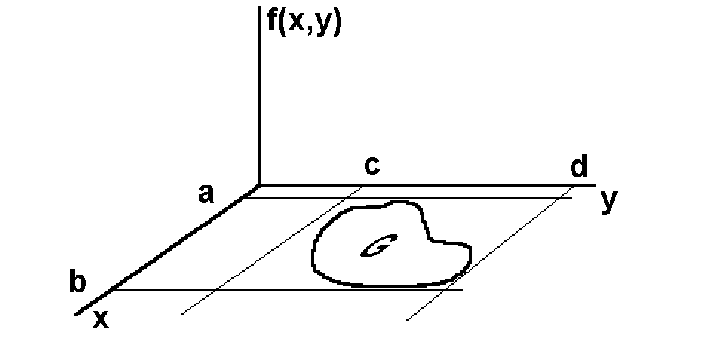
Теперь понятно, что приближенное значение интеграла будет:

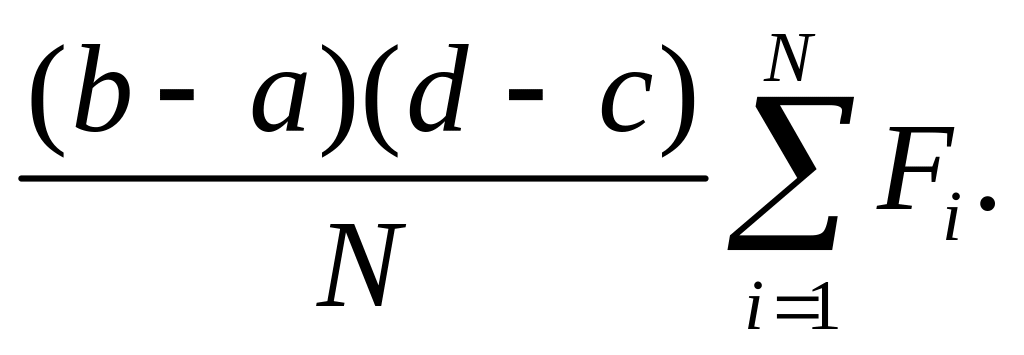
Точность вычисления интеграла зависит от значения N. Оценка ошибки вычислений универсальна во всех приложениях метода Монте - Карло. Работает она и здесь, но под значением M здесь надо понимать не полное число испытаний N, а число точек, попавших в область интегрирования G. Именно по этой причине следует выбирать минимальный по размеру прямоугольник, полностью содержащий G. Иначе большинство испытаний будет работать "вхолостую".

Второй пример на использование метода Монте - Карло в вычислительной математике относится к решению ЗАДАЧ ОПТИМИЗАЦИИ. Задача оптимизации заключается в нахождении точки многомерного пространства, доставляющей минимум или максимум функции многих переменных в заданной области изменения этих переменных. Заключительные слова последней фразы для задачи оптимизации имеют принципиальное значение. Если бы речь шла просто о поиске экстремума функции многих переменных, то это можно было бы без проблем сделать средствами классического математического анализа. Точки экстремумов находятся из условий равенства нулю всех частных производных функции по ее аргументам. Задача сразу становится решенной в принципе, поскольку сводится к решению системы уравнений. В этом случае задача снова становится неинтересной для уже знакомого нам "чистого" математика, и уже знакомый нам "чистый" математик может спокойно отправляться на уже знакомый нам диван. Однако, не относя себя к упомянутым корифеям высокой науки, мы, простые смертные, помним, что и решение систем трансцендентных уравнений вещь вовсе не простая. Но дело даже и не в этом. Проблема возникает из-за того, что минимальное или максимальное значение функции надо найти не "вообще", а в заданной области изменения переменных. Обычно эта область задается системой неравенств, ограничивающих возможные изменения аргументов функций. При этом может возникнуть ситуация, когда точка максимума лежит именно на границе этой области. Это печальное обстоятельство делает практически бесполезным для нас аппарат классического математического анализа. Следует отметить, что современная математика достигла больших успехов в разработке аналитических методов решения оптимизационных задач. Сюда относятся, например, методы линейного и целочисленного программирования, которые уже выходят за рамки классического анализа. Однако, методы эти далеко не универсальны и, зачастую, довольно трудоемки. В этой связи весьма эффективным становится использование и здесь статистических испытаний.

Нам пришлось потратить довольно много вводных слов о задаче оптимизации. В то же время сам метод Монте - Карло здесь чрезвычайно прост. Необходимо найти точку n-мерного пространства, для которой значение функции n аргументов не меньше, чем в любой другой точке заданной области в этом пространстве. По аналогии с вычислением кратных интегралов следует образовать n-мерный прямоугольный параллелепипед минимального размера, целиком содержащий заданную область. Теперь, с помощью генератора случайных, равномерно распределенных чисел, необходимо заполнить этот параллелепипед большим числом случайных точек. Рассмотрению подлежат только точки, попадающие в заданную область. Среди них не составляет труда найти точку, доставляющую минимальное (максимальное) значение.

Решение задачи Коши для обыкновенных дифференциальных уравнений

Аппарат дифференциальных уравнений, несомненно, является наиболее мощным и наиболее распространенным средством описания процессов и явлений в самых разнообразных областях. Следовательно, именно дифференциальные уравнения являются наиболее часто используемыми инструментами математического моделирования. Именно поэтому дифференциальным уравнениям в данном разделе уделено наибольшее внимание.

Предполагается, что читателю известны начальные сведения из теории обыкновенных дифференциальных уравнений (ОДУ). Освежив в памяти эти сведения, читатель вспомнит о том, что для ОДУ порядка выше первого (для определенности будем говорить об уравнениях второго порядка) возможны две принципиально различные постановки задачи решения уравнения. Если все начальные условия, определяющие, в конечном итоге, значения функции и ее производных, заданы в одной точке - на одном из концов интервала изменений независимой переменной, то говорят, что сформулирована задача Коши, или начальная задача. Если условия заданы на обоих концах интервала, на котором строится решение, то такая задача решения ОДУ называется краевой. Для уравнений первого порядка имеет смысл говорить только о начальной задаче, поскольку для них задается единственное условие.

Основное наше внимание будет уделено решению задач Коши для ОДУ. Начнем с уравнения первого порядка, которое в общем виде можно представить в форме F(y',y,x)=0 c начальным условием y(x₀)=y₀. Далее будем считать, что уравнение может быть разрешено относительно производной так, что приводится к виду:

Все методы интегрирования ОДУ в задачах Коши сводятся к приближенному вычислению последующего значения y_i в точке x_i через предыдущее значение y_i-1 в точке x_i-1, при заданном из начального условия значении y₀. В простейших случаях можно исходить из непосредственного определения понятия производной, переходя от бесконечно малых к конечным разностям:

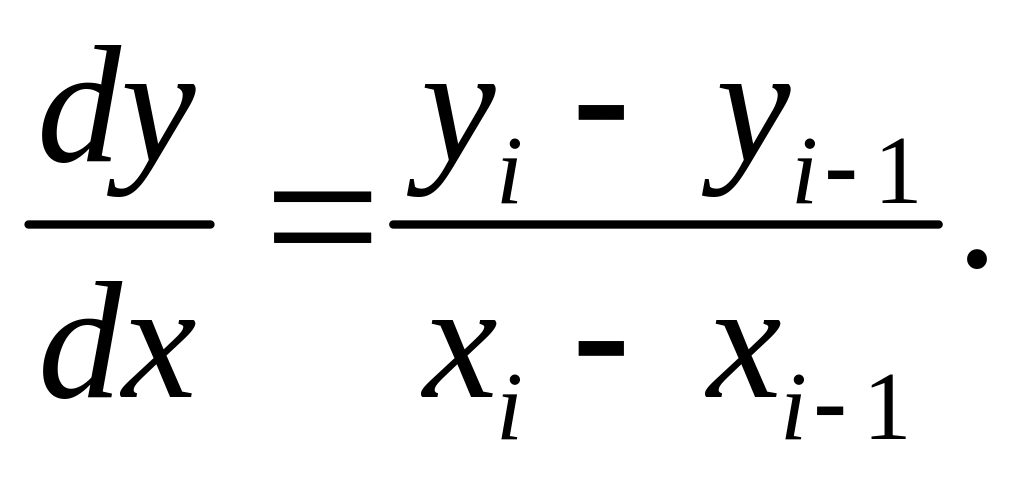
При этом нетрудно убедится, что из дифференциального уравнения

следует:

Внимательный читатель заметит, что не мешало бы поставить индексы у x и y в аргументах функции f(y,x). Читатель, несомненно, прав. Вот вопрос о том, какие индексы поставить, весьма нетривиален. Вообще-то мы можем выбрать i или i-1 для независимой переменной и искомой функции произвольно. Все равно приближенное равенство должно быть справедливым. Обе возможности, действительно, можно реализовать. Если выбор за индексом i-1, то получаем формулу МЕТОДА ЭЙЛЕРА:

В противном случае имеем формулу НЕЯВНОЙ СХЕМЫ:

С вычислениями по схеме Эйлера не возникает никаких проблем, поскольку следующее значение y_i непосредственно находится из правой части равенства, содержащего известное предыдущее значение y_i-1. С неявной схемой дело обстоит сложнее. Искомая величина y_i присутствует как в левой, так и в правой частях равенства. Очевидно, далеко не для всякого вида функции f(y,x) выражение можно разрешить относительно последующего значения и привести его к виду y_i=Ф(y_i-1, x_i,x_i-1). Выбор в пользу метода Эйлера или неявной схемы необходимо делать не только с точки зрения простоты вычислений. В конце концов, мы уже научились решать трансцендентные уравнения, и, даже если формулу неявной схемы не удается разрешить относительно y_i, численные методы помогут решить эту проблему. Есть, однако, более серьезные обстоятельства, которые заставляют в некоторых случаях отдать предпочтение неявной схеме. Для выяснения этих моментов нам необходимо рассмотреть новое понятие, имеющее важнейшее значение для численного решения дифференциальных уравнений.

Понятие, о котором идет речь, называется устойчивостью численной схемы. Если схема предполагает вычисление последующего значения функции через предыдущее, как это и имеет место в двух описанных методиках, то следует быть уверенным, что в вычислительном процессе не происходит накопление ошибки. Если не вдаваться в детали, то ситуацию можно представить следующим образом. Приближенные вычисления по любой из схем вносят на каждом шаге ошибку. В зависимости от вида схемы эта ошибка может либо каждый раз иметь один и тот же знак, либо знак может случайным образом меняться. В первом случае, очевидно, происходит накопление ошибки, и численное решение очень быстро уходит от истинного. Тогда говорят, что вычислительная схема неустойчива и ее применение, разумеется, некорректно. Во втором случае ошибки в среднем взаимно компенсируются, их накопление от шага к шагу не происходит, и схема называется устойчивой. Устойчивость схемы зависит от многих факторов. На нее влияет и величина шага интегрирования, и вид функции f(y,x), и структура правой части равенства y_i=..... Математики научились анализировать устойчивость вычислительных схем. Результат такого анализа, применительно к нашим задачам, констатирует тот печальный факт, что безусловно устойчивой является именно менее удобная неявная схема, в то время, как "хорошая" схема Эйлера может оказаться всегда неустойчивой или устойчивой только при неоправданно малом шаге интегрирования. Здесь все зависит уже от конкретного вида функции f(y,x). В этой связи автор призывает относиться весьма осторожно к результатам, полученным простыми методами решения ОДУ. Если при моделировании какого-либо процесса с помощью численного интегрирования уравнений, вы получили результат, который, как говорится, не лезет ни в какие ворота, не ограничивайтесь только поиском ошибок в программе для компьютера. Возможно, причина ваших неудач лежит глубже - выбрана некорректная вычислительная схема.

Рассмотренные два метода, несмотря на свою простоту, не следует применять в серьезных задачах, прежде всего, в силу их недостаточной точности (даже если забыть об этой "занозе" - проблеме устойчивости). Для расчетов на профессиональном уровне наиболее часто используются средства из группы методов РУНГЕ-КУТТА. Для большинства задач наиболее оптимальным из этой группы является метод Рунге-Кутта четвертого порядка, который достаточно прост в реализации, имеет высокую точность и хорошую устойчивость. Мы по-прежнему рассматриваем дифференциальное уравнение первого порядка y'=f(x,y) с начальным условием y(x₀)=y₀. Для решения выбирается достаточно малый постоянный шаг изменения независимой переменной h так, что очередное значение x_i есть x_i-1+h=x₀+ih, где i=1,2,3,.... Очередное значение искомой функции определяется из предыдущего по формуле:

где коэффициенты k на каждом шаге определяются через значения функции f(x,y) при определенных значениях аргументов:

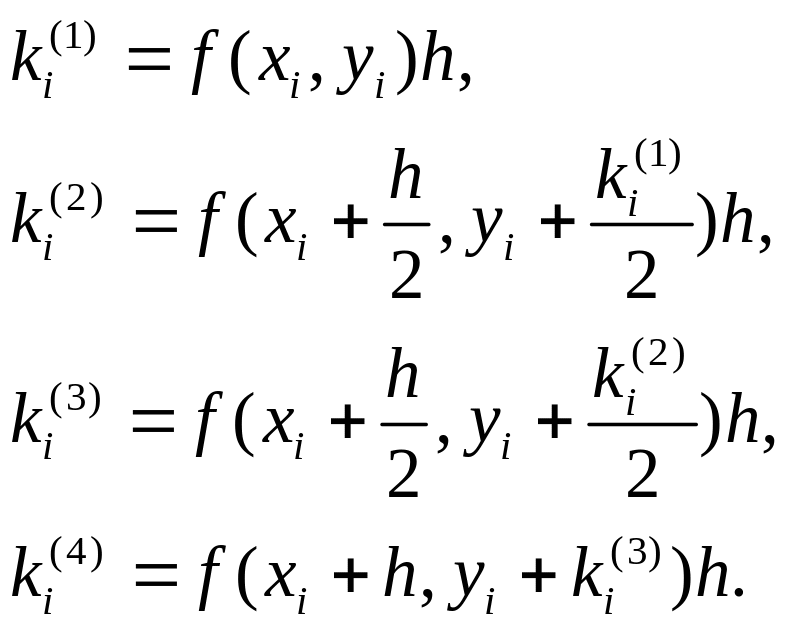
Можно видеть, что на каждом шаге сначала вычисляются коэффициенты в той последовательности, в которой они указаны (поскольку они вычисляются один через другой), а затем определяется очередное значение функции.

Для достижения необходимой точности используется уменьшение величины шага интегрирования. Поскольку наибольшую ошибку вычислений следует ожидать в конечной точке интервала изменения независимой переменной, именно здесь следует оценивать относительную ошибку, сравнивая, например, результаты расчетов с заданным и уменьшенным вдвое значением шага интегрирования.

Мы рассмотрели методики решения уравнений первого порядка. На очереди уравнения порядка выше первого и системы дифференциальных уравнений. Задача Коши для уравнения n - го порядка формулируется следующим образом. Дано дифференциальное уравнение F(x,y,y',y'',...,y⁽ⁿ⁾)=0. В точке x₀ должны быть заданы значения искомой функции y(x₀)=y₀₀ и всех производных до n-1 порядка, включительно y^(p)(x₀)=y_0p, p=1,2,...,n-1.

Далее уравнение n - го порядка сводится к системе n уравнений

первого порядка. Для этого обозначим y₁=y', y₂=y''=y₁', y₃=y'''=y₂',... y_n=y⁽ⁿ⁾=y_n-1'. Кроме того, для единообразия обозначим y через y₀. Теперь мы имеем следующую систему уравнений первого порядка с начальными условиями:

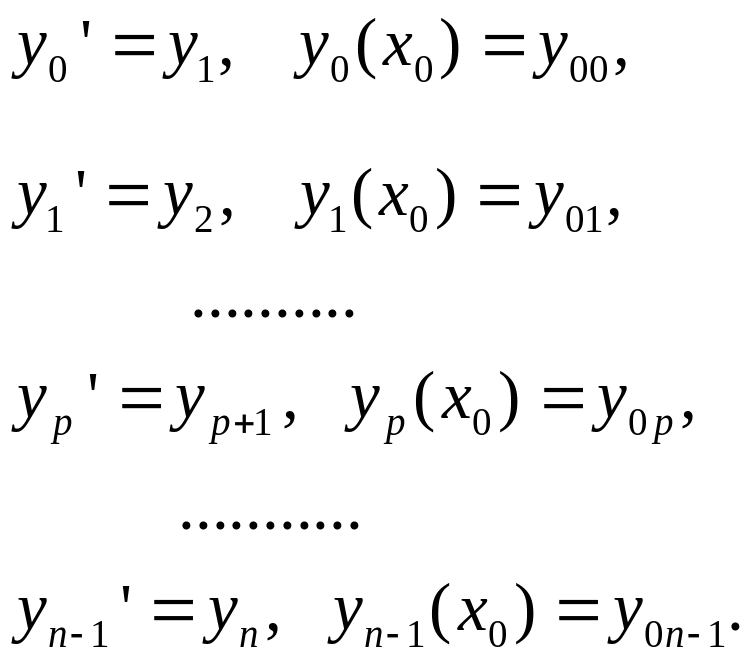
Система дополняется последним уравнением, полученным из исходного дифференциального уравнения, разрешенного относительно старшей производной:

Продемонстрируем сведение уравнения второго порядка к системе на примере следующей задачи. Имеется дифференциальное уравнение y''+y'+y=y²sin(x) с начальными условиями y(x=0)=A, y'(x=0)=B. Обозначаем y₀=y, y₁=y'=y₀'. Получаем систему:

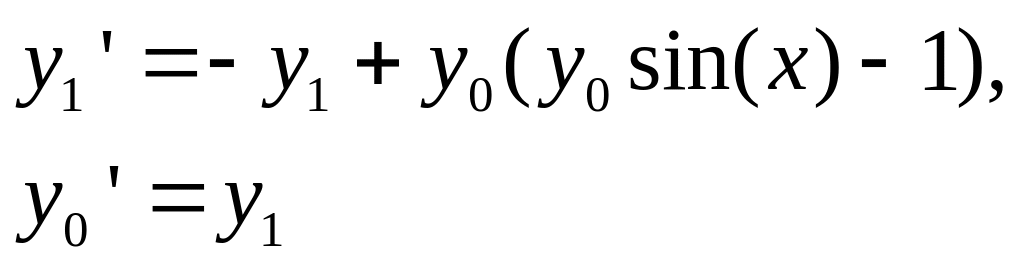
при начальных условиях y₀(x=0)=A, y₁(x=0)=B.

В общем виде задача Коши для системы дифференциальных уравнений первого порядка записывается в виде:

Здесь i - номер уравнения в системе. Решение по методу Рунге-Кутта четвертого порядка строится по формуле:

Индекс р обозначает номер точки на оси Ох. Коэффициенты k аналогично тому, как это делалось для одного уравнения, на каждом шаге вычисляются по формулам:

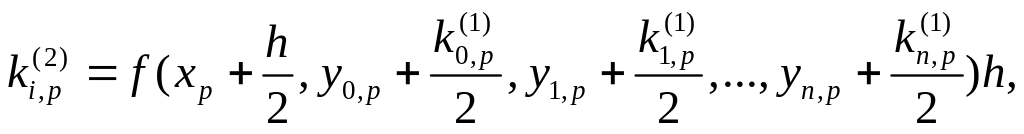
Таким образом, перемещаясь от точки к точке по координате x – от номера p к номеру p+1 мы получаем табличное численное решение системы дифференциальных уравнений.

Метод Рунге – Кутта четвертого порядка действительно широко используется на практике в задачах решения дифференциальных уравнений, поскольку обладает хорошей устойчивостью и достаточной точностью. В особых случаях, когда предъявляются повышенные требования к точности решения, могут быть использованы методы более высоких порядков, свдения о которых можно получить из литературы по вычислительной мптематике.

Ряды и дифференциальные уравнения

Несмотря на то, что существуют объемные справочники в которых можно найти большое количество решений различных дифференциальных уравнений, представленных через элементарные функции, такие "счастливые случаи" следует считать скорее исключениями из правил для большинства конкретных прикладных задач. Очень часто для получения решений, в том числе и при компьютерном моделировании процессов и явлений, приходится прибегать к тем или иным вычислительным методам. Существует, однако, большой класс обыкновенных дифференциальных уравнений, решения которых хотя и не представляются через элементарные функции, тем не менее, могут быть решены специальными способами, относящимися все-таки к точным методам (в отличие от приближенных, численных). Речь идет о решении уравнений с помощью степенных рядов. Построенные такими способами решения выражаются через так называемые специальные функции, которые когда-то на фоне старых добрых элементарных функций вроде экспоненты, синуса и косинуса представлялись "экзотическими" объектами, из-за чего и получили свое название. Поскольку специальные функции позволяют представить решения уравнений, моделирующих многие физические явления мы сочли необходимым коротко познакомить читателя с существом вопроса не вдаваясь, впрочем, в математические тонкости и во многом пожертвовав строгостью изложения материала.

Типичной задачей, приводящей к использованию степенных рядов при решении дифференциальных уравнений, является решение уравнения Бесселя, которое нашло множество применений при рассмотрении различных проблем, в том числе и технического характера. Рассмотрим формальную, математическую сторону вопроса - интегрирование обыкновенных дифференциальных уравнений с помощью степенных рядов. Сразу отметим, что в "чистом виде" этот метод применим к линейным дифференциальным уравнениям у которых в качестве коэффициентов при производных и самой неизвестной функции, а также в правой части уравнения стоят ряды по степеням независимой переменной. Хотя современная математика уже далеко ушла от этого самого "чистого вида", мы ограничимся именно этим каноническим случаем. Более того, рассматриваемый способ мы проиллюстрируем только одним конкретным примером - решением уравнения Бесселя.

"Классическая" запись уравнения Бесселя представляется в следующем виде:

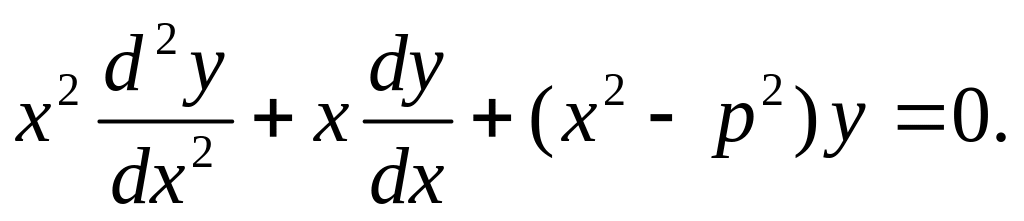
Помимо независимой переменной x, искомой функции y в уравнение входит постоянная величина p, которая может принимать любые комплексные значения. Как можно видеть, коэффициенты при производных и функции действительно представляют собой степенные функции от х, что и позволит применить метод интегрирования с помощью степенных рядов.

Будем искать решение уравнения в виде:

где b - пока не определенная постоянная. В таком представлении производные искомой функции задаются соотношениями:

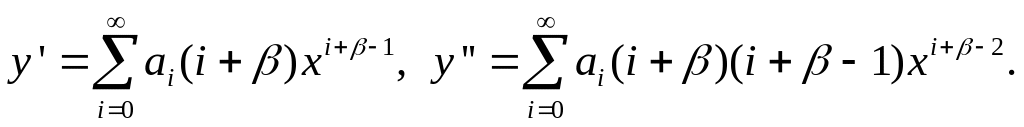
После подстановки этих выражений в основное уравнение, последнее может быть представлено следующим образом:

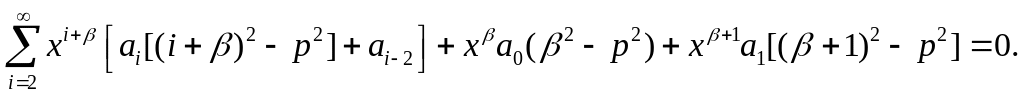
Все дальнейшие выводы следуют из того факта, что последнее равенство должно тождественно выполняться для любых значений х. Тогда следует приравнять нулю коэффициенты при всех степенях х. Из этого условия для первого слогаемого суммы получается соотношение:

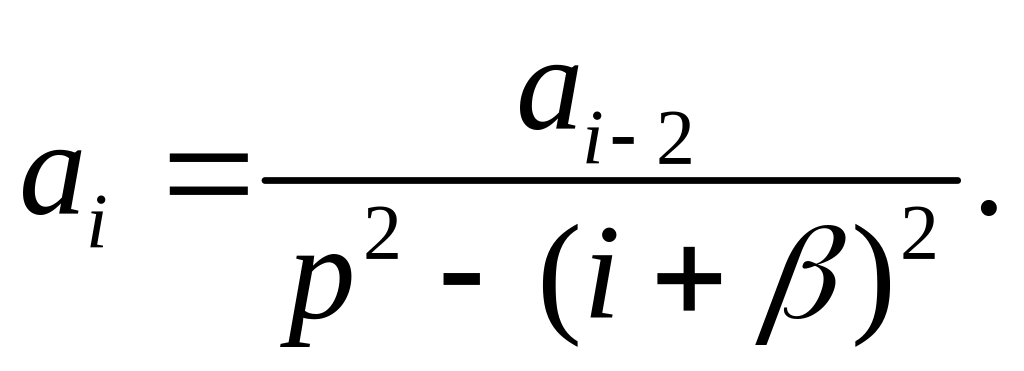
С двумя оставшимися слагаемыми уравнения можно обойтись следующим способом. Выберем представления двух начальных коэффициентов ряда поочередно в виде пар a₀=0, a₁=1 и a₀=1, a₁=0. Для первой пары следует потребовать выполнения равенства:

а для второй пары, соответственно:

Отсюда определяются два возможных значения величины b₁= p, b₂= -p, использование которых дает два линейно независимых решения уравнения Бесселя. Для конструирования решений у нас имеется рекуррентное соотношение, связывающее с и начальный коэффициент a₀=1. Не составит большого труда убедиться в том, что использование другой пары коэффициентов a₀, a₁ даст точно такие же ряды.

Окончательно два линейно независимых решения исходного уравнения задаются функциями:

которые получили название функций Бесселя первого и второго рода. Общее решение уравнения Бесселя компонуется из линейно независимых решений обычным образом в виде C₁J_p(x)+C₂J_-p(x).

Мы упоминали о том, что величина p может быть произвольной комплексной константой. Однако в последних выражениях используются факториалы от величин, содержащих p. Ничего страшного в этом нет, поскольку в математике "школьное" понятие факториала, как функции от целого аргумента, расширено и на нецелые и на отрицательные и даже на комплексные числа. При этом факториал обычно называют другим именем - гамма-функция, которая также относится к классу специальных функций.

С помощью функций Бесселя конструируются решения дифференциальных уравнений в задачах так или иначе связанных с цилиндрической (или полярной) системой координат. По этой причине бесселевые функции часто называются также цилиндрическими функциями. Представление о характере функций Бесселя дает приведенный ниже рисунок, где изображены две цилиндрические функции при значениях порядка р равных 0 и 1.

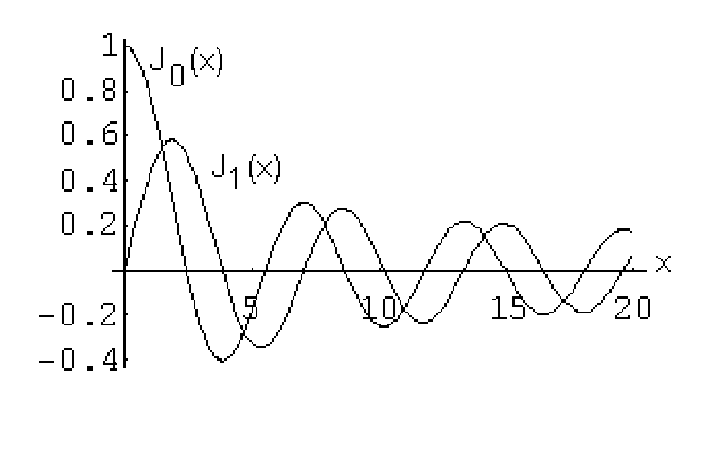
Для вычисления значений бесселевых функций мы имеем их представления с помощью степенных рядов. Как осуществить эту процедуру практически? На первый взгляд кажется очевидной возможность непосредственного использования представленных формул. Однако такая попытка очень быстро приведет к тому, что вычислительный алгоритм столкнется с необходимостью вычисления больших числовых значений, образующихся в знаменателях выражений, составляющих суммы - факториал (и гамма-функция) является крайне быстро возрастающей функцией своего аргумента. Кроме того, при этом остается открытым вопрос о том, как обойтись с "суммированием до бесконечности".

Прежде всего, заметим, что ряды, представляющие бесселевы функции, как и другие специальные функции, являются сходящимися, то есть суммы здесь стремятся к ограниченному пределу. Дело в том, что в силу быстрого увеличения знаменателей в суммах величина очередного члена ряда стремится к нулю при возрастании номера члена при любых конечных значениях х. Хотя это еще и не является достаточным условием сходимости, тем не менее, эта сходимость имеет место - с этим математики уже давно разобрались. Тогда сумма конечного, но достаточно большого числа членов ряда даст приближенное значение функции. Если необходимо вычислить ряд с заданной относительной точностью e, то суммирование членов ряда S необходимо выполнять до тех пор, пока выполняется неравенство:

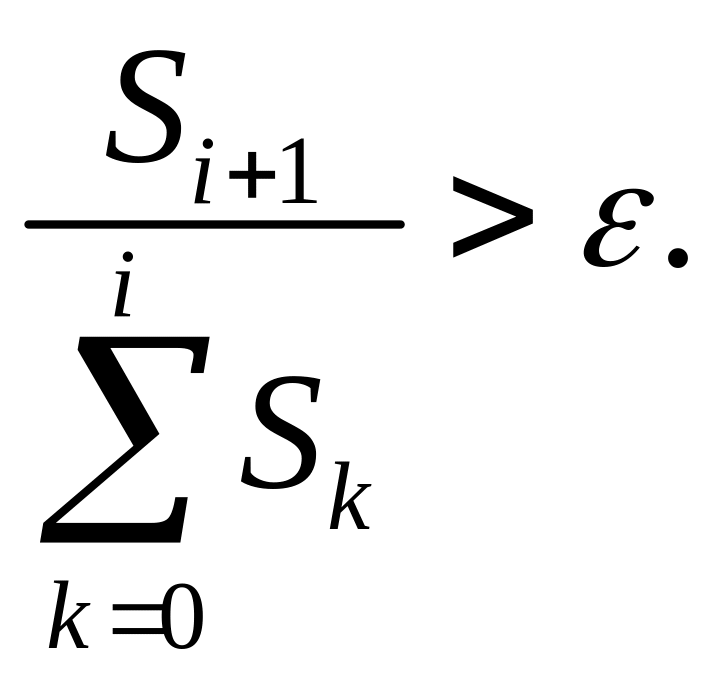
При расчетах на компьютере можно потребовать вычисления рядов с максимально высокой, так называемой "машинной" точностью. Рано или поздно при вычислении частного от деления в очередном члене ряда будет образован машинный ноль - малое число, которое уже не может быть представлено в разрядной сетке вычислительного устройства. Вот до реализации этой ситуации и можно продолжать суммирование ряда, хотя, как правило, в большинстве конкретных задач столь высокая точность является избыточной.

Что касается самого алгоритма суммирования ряда, то здесь, безусловно, необходимо использовать рекуррентное соотношение, позволяющее находить значение последующего члена ряда через предыдущее. Только таким способом можно избежать "вычислительных неприятностей", о которых говорилось выше. Так, для первого ряда такое рекуррентное соотношение и необходимое начальное значение задаются следующим образом:

Полезно отметить, что во всех системах программирования и специализированных пакетах для вычисления не только специальных, но и элементарных функций используется именно алгоритм рекуррентных вычислений с машинной точностью. Так, показательная функция (экспонента) вычисляется с помощью представления ее в виде разложения в ряд Тейлора:

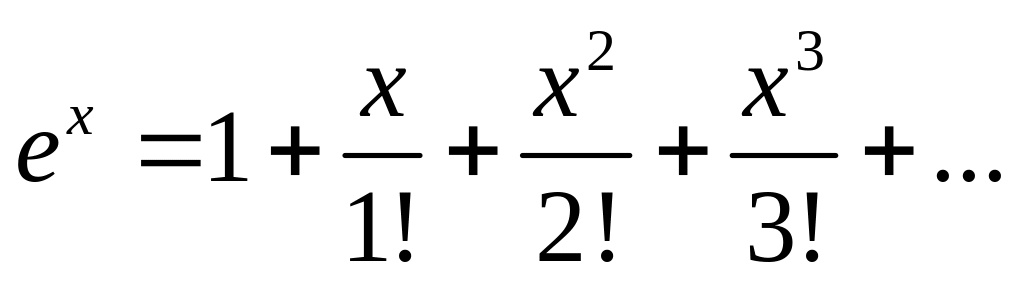
так, что последующий член ряда выражается через предыдущий по формуле:

Разложение в ряд Тейлора функции sin(x) выглядит следующим образом:

Следует отметить, что этот ряд может быть получен и как одно из решений дифференциального уравнения

Второе линейно – независимое решение для этого уравнения задается рядом

Как легко проверить, этот ряд представляет собой разложение по Тейлору функции cos(x).

Задачи с краевыми условиями для дифференциальных уравнений

Перейдем от задач Коши к задаче с краевыми условиями. Мы рассмотрим только линейную задачу для уравнения второго порядка. Задача формулируется следующим образом. В области a<x<b найти функцию y(x), удовлетворяющую уравнению:

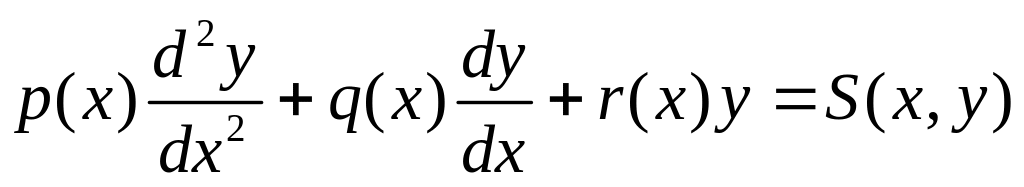
и краевым условиям, заданным на левом и правом концах интервала:

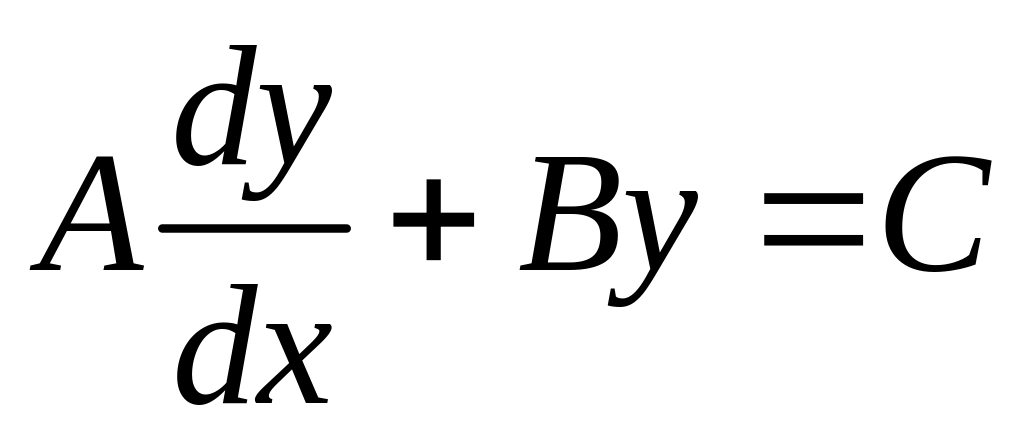при

при

В уравнении p(x), q(x), r(x) - произвольные (в угоду математикам следует добавить: "достаточно хорошие") функции независимой переменной, S(x,y) - линейная по y функция. В краевых условиях A, B, C, D, E, F – постоянные величины. Для численного решения интервал [a,b] разбивается на малые подынтервалы длиной h, и производные заменяются их приближенными конечно-разностными аналогами:

Происхождение таких разностных представлений достаточно очевидно и поясняться не будет. Подставляя последние соотношения в уравнение и в краевые условия, можно убедиться, что, в общем виде, переход от бесконечно малых к конечным разностям в линейной краевой задаче для уравнения второго порядка дает:

Здесь N - число разбиений интервала [a,b].

Последние соотношения представляют собой ни что иное, как систему из N+1 линейных алгебраических уравнений с N+1 неизвестными (величины y₀, y₁,...,y_N). Решение систем линейных алгебраических уравнений вроде бы не должно встречать никаких трудностей - это классическая и давно решенная проблема линейной алгебры. Трудности могут возникнуть на практике. Если нам приходится делать большим число разбиений N, делая, тем самым, большим число уравнений, то при реализации на компьютере известных методик решений с использованием различных преобразований матриц мы неизбежно столкнемся с непреодолимыми проблемами типа переполнений, потерь точности и тому подобными. К счастью, в рассматриваемом нами случае можно, в конечном итоге, вообще обойтись без матриц, поскольку для подобных задач был найден надежный, оперативный и экономичный по ресурсам машинной памяти МЕТОД ПРОГОНКИ.

Нашу систему линейных уравнений можно представить в матричном виде G*Y=Z, где G - матрица коэффициентов системы, Y - искомый вектор, Z – вектор правых частей системы. Замечательным является то, что матрица G в нашем случае является трехдиагональной, то есть в ней ненулевыми являются только элементы главной и двух соседних диагоналей. Именно для задач с трехдиагональной матрицей и разработан метод прогонки.

Вывод формул метода прогонки настолько прост, что на него не стоит тратить время. Сразу сформулируем алгоритмическую сторону метода. Расчеты производятся в два "прогона" - туда и обратно, откуда и произошло название метода. В прямом прогоне последовательно, шаг за шагом, вычисляются пары коэффициентов  и  по формулам:

Расчеты проводятся для i=1, 2, 3,...,N-1 при начальных значениях ₁=k₁, ₁=m₁. Далее вычисляется значение искомой функции на правом конце:

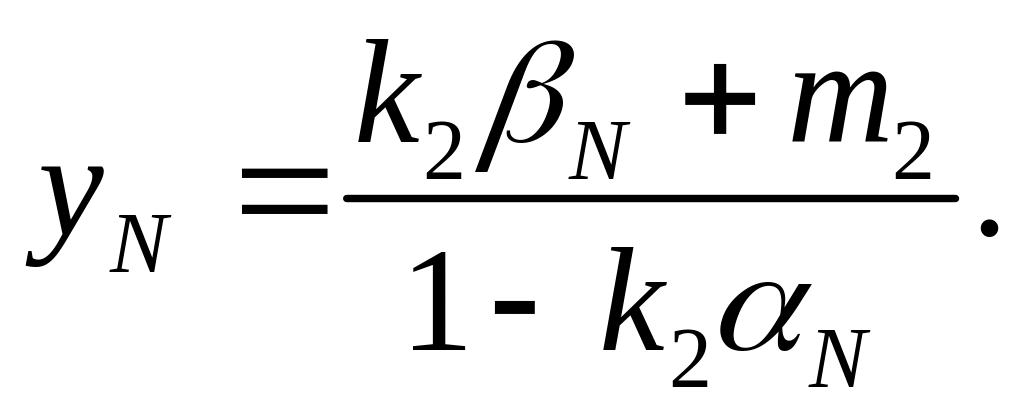
После этого в обратном прогоне находятся все остальные значения:

Как можно видеть, краевая задача с помощью метода прогонки решается, пожалуй, даже проще, чем задача Коши в методе Рунге-Кутта. К сожалению, в части устойчивости решения такое сравнение будет явно не в пользу краевых задач. В этой связи автор снова призывает тех, кому на практике придется заниматься такого сорта задачами, быть осторожными.