1. Теоретична частина

Мета: у процесі вирішення завдань засвоїти основні положення теорії відображення поверхні земного еліпсоїда на поверхні кулі.

Посібник: підручник - Вахромєєва Л.А., Бугаєвський Л.М., Козакова З.Л. «Математична картографія» (с. 22 - 43) або підручник - Вахромєєва Л.А. «Картографія» (с. 15 - 29), довідник з математики.

Завдання: на основі заданих рівнянь проекцій визначити вид сітки меридіанів і паралелей, ортогональность сітки, приватні масштаби і спотворення кутів, групу проекцій за характером спотворень. По заданих рівнянь знайти опис проекції в підручниках, вказати сторінки.

Кожен студент отримує завдання, яке складається з двох рівнянь картографічної проекції. Вид рівняння визначається за номером варіанта (Додаток А).

Далі, дотримуючись наступного алгоритму, вирішуємо задачу на загальну теорію зображення.

1. Визначаємо вид сітки меридіанів і паралелей на основі аналізу рівнянь меридіанів та паралелей. Із загальної теорії картографічних проекцій відомо, що:

- рівняння паралелей (1)

- рівняння меридіанів (2)

Отже, рівняння, отримані за номером варіанту, необхідно привести до виду (1) і (2), тобто для отримання рівняння меридіанів із заданих рівнянь треба виключити широту , а для отримання рівняння паралелей - довготу .

Для отримання рівняння меридіанів та паралелей виконують відповідні алгебраїчні перетворення.

2. Визначимо ортогональність картографічної сітки. Умовою ортогональності сітки є вираз:

(3)

Знаходимо похідні від х та у, і перевіряємо, дорівнює їх сума нулю чи ні. Якщо дорівнює, то сітка ортогональна.

3. Обчислимо часткові масштаби вздовж паралелей і меридіанів, масштаб площ, спотворення кутів. Із загальної теорії відображення поверхні еліпсоїда на кулі відомо:

масштаб вздовж меридіана (4)

масштаб вздовж паралелі (5)

- коефіцієнт Гауса (6)

- коефіцієнт Гауса (7)

Масштаб площ обчислюють за формулою:

(8)

де a, b – екстремальні масштаби;

а=(А+В)/2 b=(А-В)/2 (9)

(10)

і - кут між меридіанами і паралелями в проекції, обчислюють за формулою:

(11)

Спотворення кутів:

(12)

4. Визначимо групи проекцій за характером спотворень. Умова рівнокутні:

f=0; m=n; =0 (13)

Умова рівновеликості для кулі:

(14)

Після визначення групи проекції, необхідно привести її зображення та зробити висновки.

2. Практична частина

2.1 Приклад 1

Картографічна проекція задана рівняннями:

1. Визначаємо вид сітки меридіанів і паралелей на основі аналізу рівнянь меридіанів та паралелей.

Отже, рівняння, отримані за номером варіанту, необхідно привести до виду (1) і (2), тобто для отримання рівняння меридіанів із заданих рівнянь треба виключити широту , а для отримання рівняння паралелей - довготу .

Для отримання рівняння меридіанів та паралелей виконують алгебраїчні перетворення.

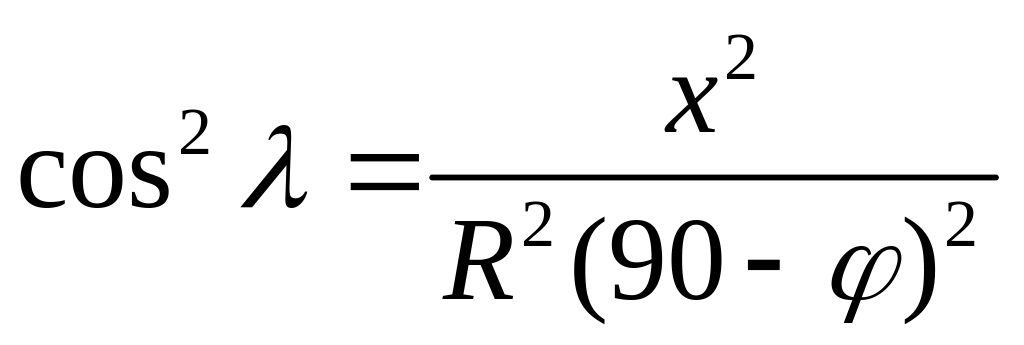
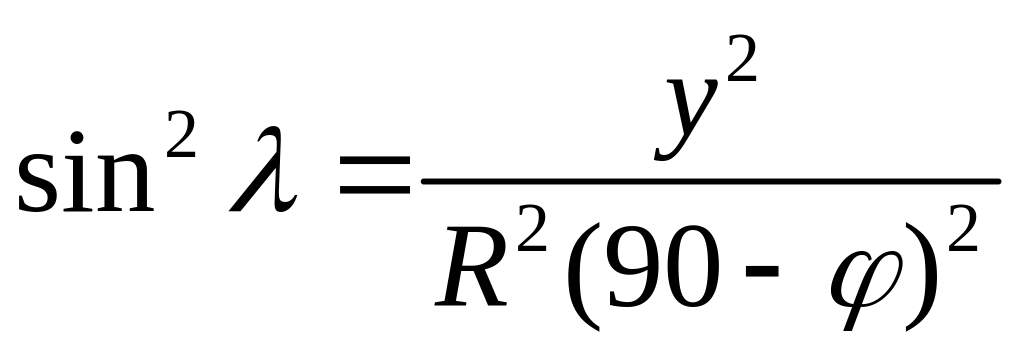
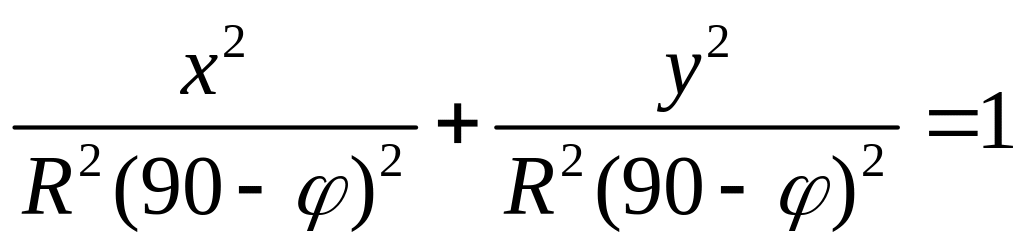– рівняння паралелей

– рівняння меридіанів

2. Визначимо ортогональность картографічної сітки. Умовою ортогональності сітки є вираз (3). Знайдемо похідні:

Для нашого прикладу:

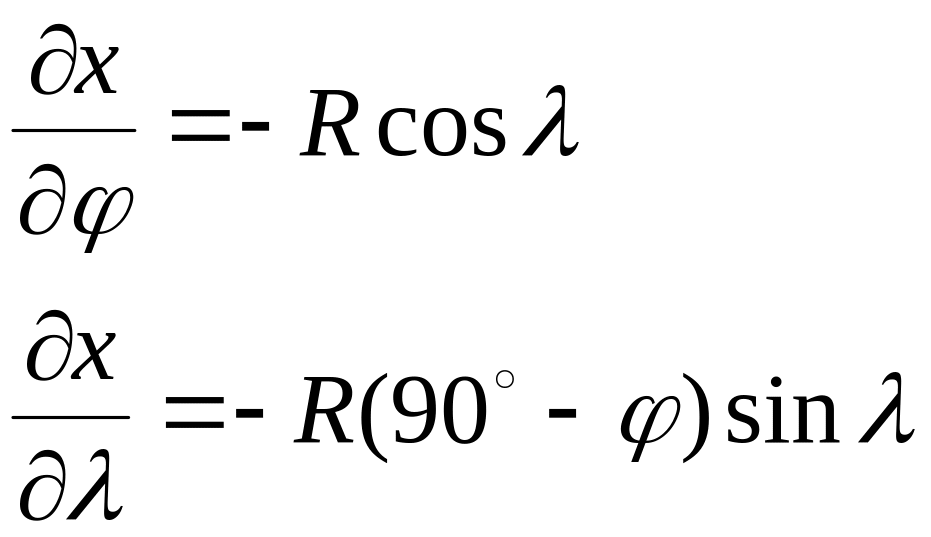
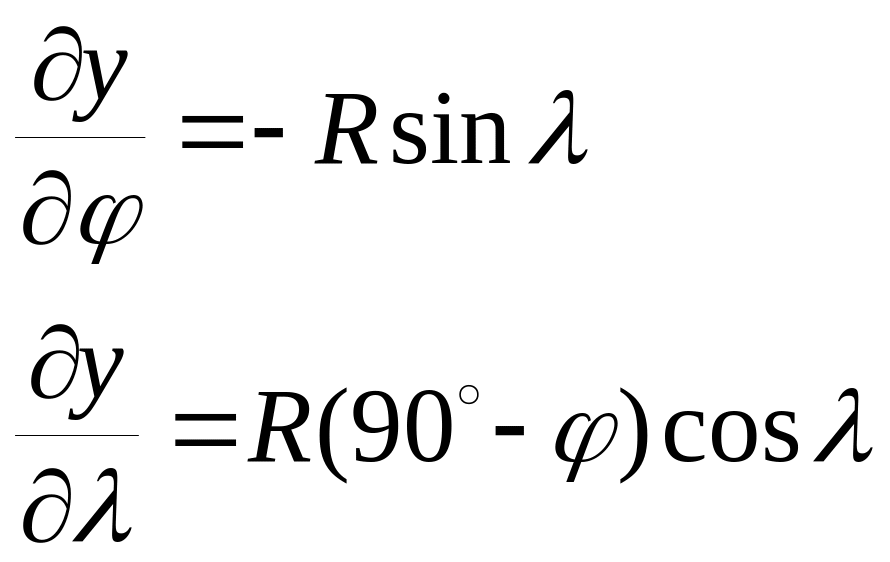
Сітка ортогональна.

3. Обчислимо приватні масштаби вздовж паралелей і меридіанів, масштаб площ, спотворення кутів.

На підставі формул (4 – 7) отримуємо:

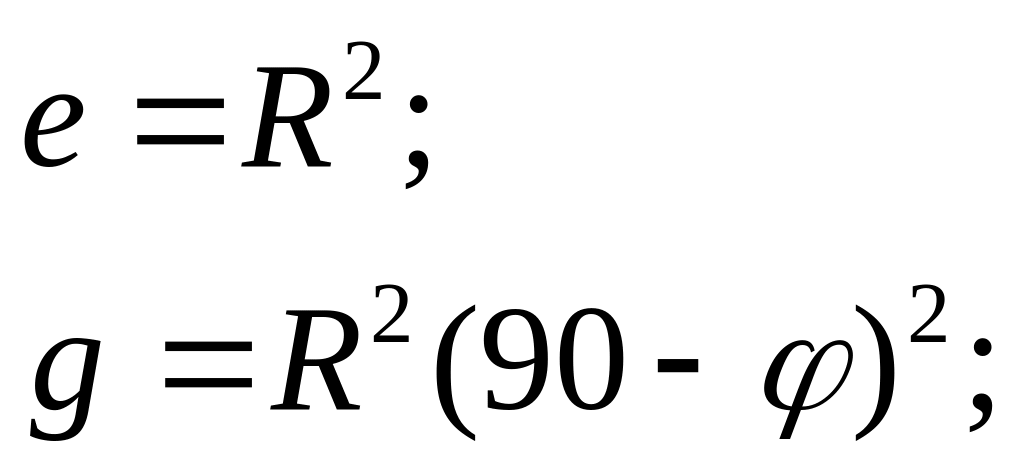
- масштаб вздовж меридіанів;

- масштаб вздовж паралелей.

За формулами (8 – 11) отримуємо наступні значення:

Спотворення кутів отримуємо за формулою (12):

4.Визначимо групи проекцій за характером спотворень. Умова рівнокутності визначається за формулою (13).

У нашому випадку f=0 , а mn, 0 тобто проекція не рівнокутна.

Перевіряємо умову рівно великості для кулі за формулою (14).

У нашому випадку проекція не рівновелика.

Розглянута проекція є рівнопроміжна азимутальна. У такій проекції меридіани нормальної сітки прямі, що перетинаються в одній точці під кутами, рівними різниці відповідних довгот, а паралелі - концентричні кола з центром у точці перетину меридіанів.

Нормальні азимутальні проекції рекомендуються для створення карт полярних територій.

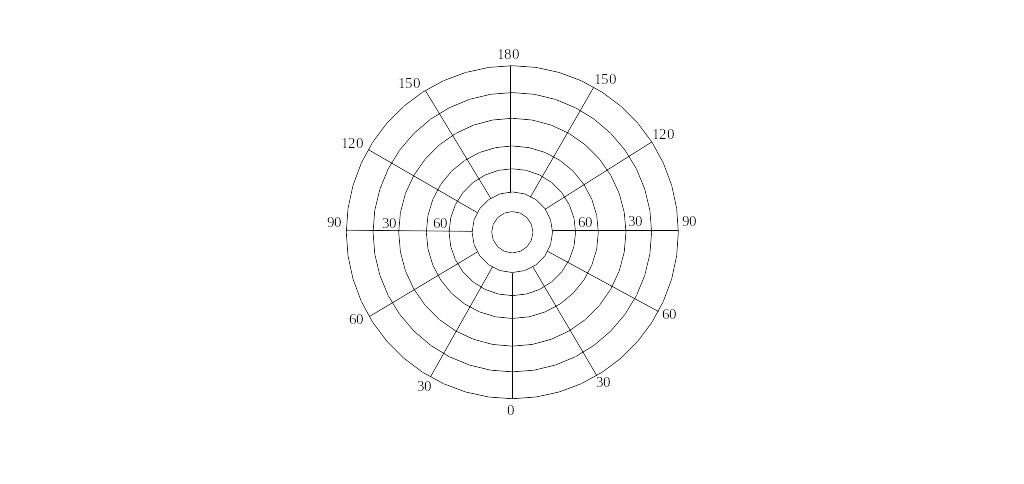
Рисунок 1 – Рівнопроміжна за меридіанами нормальна азимутальна проекція

Висновки:

1. Вид сітки меридіанів і паралелей на підставі аналізу рівняння меридіанів і паралелей:

– рівняння паралелей

– рівняння меридіанів

2. Ортогональність картографічної сітки:

f = 0, сітка ортогональна.

3. Приватні масштаби вздовж меридіанів і паралелей:

- масштаб вздовж меридіанів - рівнопроміжна за меридіанами

- масштаб вздовж паралелей.

Масштаб площ:

Спотворення кутів:

4. Групи проекцій за характером спотворень: