Глава 5.

Система статистичних показників

5.1. Основні теоретичні положення

1. Абсолютні величини – статистичні показники, які характеризують розміри досліджуваного явища (ознаки); складають основу статистичного спостереження.

Абсолютні величини поділяють на:

а) у залежності від ступеню агрегування явищ:

- індивідуальні;

- сумарні;

б) у залежності від змісту досліджуваних явищ:

- натуральні (прості і складені);

- грошові;

- трудові.

2. Відносні величини – статистичні показники, що визначаються як частка від ділення двох і більше абсолютних величин і можуть бути поданими як коефіцієнт, процент, проміле, дециміле, характеризуючи розмір порівняної величини, що припадає на певний умовний розмір величини-бази порівняння.

Змістовно вони характеризують:

- виконання планового завдання; - координацію;

- динаміку; - порівняння;

- структуру; - інтенсивність.

3. Середні величини – узагальнюючі статистичні показники, що відображають дію загальних умов, закономірність досліджуваного явища й обчислюються на основі масових однорідних даних правильно статистично організованого масового спостереження, як середнє.

4. Середнє ( ) – узагальнююча числова характеристика розташування набору елементів (одиниць статистичної сукупності); якщо набір складається з елементів x₁, x₂, …, x_N, то їх середнє позначається як і може бути степеневим (незваженим і зваженим), інтегральним, логарифмічним , хронологічним.

5. Степеневе середнє (незважене, або просте) – середнє додатних чисел x₁, x₂, …, x_N, яке обчислюється за формулою:

(5.1)

де z ≠ 0 – фіксоване дійсне число; при z = -1, z = 1 і z = 2 степеневе середнє дає відповідно гармонічне, арифметичне і квадратичне середнє, а при z → 0 – геометричне середнє.

6. Степеневе середнє (зважене) – середнє величин x₁, x₂, …, x_m, що мають відповідні ваги f₁, f₂, …, f_m, яке обчислюється за формулою:

(5.2)

де зміст z аналогічний.

7. Хронологічне середнє (часове середнє) – середнє моментного ряду динаміки об’єму N з рівновіддаленими датами:

(5.3)

8. Середнє у варіаційному ряду. У варіаційних рядах найчастіше обчислюються такі середні:

- середнє арифметичне;

- середнє гармонічне;

- структурні середні.

9. Середнє арифметичне – вид степеневого середнього (z = 1), що показує, яка величина із сумарного значення ознаки в рівній мірі припадає на кожну одиницю досліджуваної статистичної сукупності.

10. Середнє арифметичне в дискретному ряду – це середнє арифметичне зважене, в якому вагами є абсолютні (відносні) частоти f_j (ω_j) відповідних індивідуальних значень x_j дискретної ознаки X:

(5.4)

11. Середнє арифметичне в інтервальному ряду – це середнє арифметичне зважене, в якому вагами є абсолютні (відносні) частоти f_j (ω_j) інтервальної ознаки, а сама ознака X представлена її серединними значеннями x_j´ в інтервалах:

(5.5)

12. Середнє гармонічне – вид степеневого середнього (z = -1), що застосовується, коли статистичні дані не містять інформації про частоту f_j окремих варіантів x_j ряду, а представлені як їх добуток W_j = x_j f_j у зваженій формі середнього:

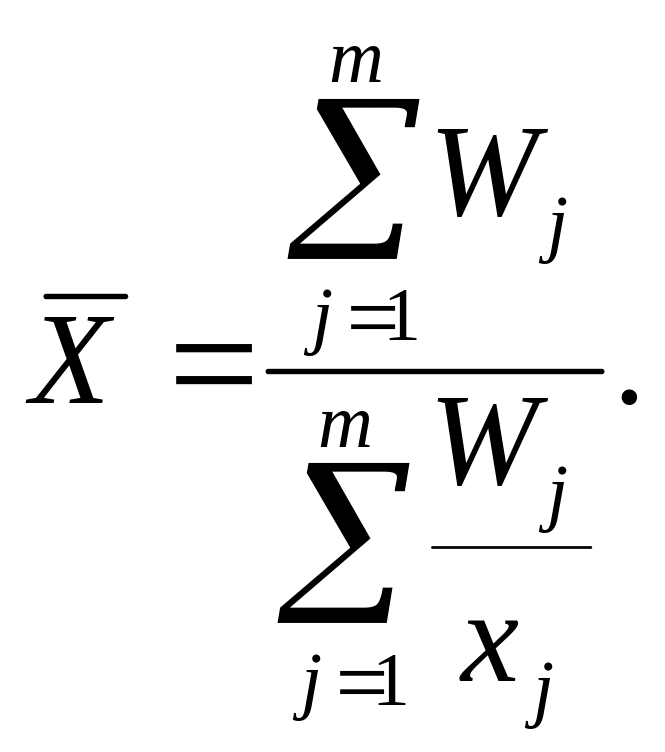(5.6)

Якщо W_j = const, то зважена форма спрощується до незваженої (простої):

(5.7)

13. Середнє альтернативної ознаки – дорівнює частці ω₁ тих варіантів, що мають досліджувану ознаку (при статистичному вираженні коливань альтернативної ознаки її наявність позначається одиницею (1), а її відсутність – нулем (0), а їх частості зручно представити як ω₁ і ω₀; ω₁ + ω₀ ≡ 1):

(1 ∙ ω₁ + 0 ∙ ω₀) : (ω₁ + ω₀) = ω₁. (5.8)

Воно не може бути більшим за одиницю.

14. Структурні середні у варіаційних рядах. До них належать мода М_о і медіана М_е.

15. Мода в дискретному ряду (М_о) – варіант з найбільшою абсолютною (відносною) частотою:

М_о = Х(f_max). (5.9)

Якщо такий варіант один, розподіл є одномодальним (унімодальним), якщо їх два – бімодальним, більше двох – багатомодальним.

16. Мода в інтервальному ряду (М_о) – умовне значення ознаки в межах модального інтервалу, або абсциса локального максимуму гістограми, яка обчислюється:

(5.10)

де х_Мо – нижня границя модального інтервалу;

Δ_Мо – довжина модального інтервалу;

f_Мо – частота модального інтервалу;

f_Мо-1 – частота інтервалу, що передує модальному інтервалу;

f_Мо+1 – частота інтервалу, наступного за модальним інтервалом.

17. Модальний інтервал – в інтервальному ряду інтервал з найбільшою абсолютною (відносною) частотою.

18. Медіана в дискретному ряду (М_е) – значення ознаки, що ділить ряд на дві рівні за об’ємом частини, або квантиль порядку ½ (М_1/2): якщо об’єм ряду непарне число, модою є центральний варіант; якщо об’єм ряду парне число, то модою є півсума двох сусідніх варіантів, між яким знаходиться медіана.

19. Медіана в інтервальному ряду (М_е) – умовне значення ознаки в межах медіанного інтервалу, що ділить об’єм ряду навпіл й обчислюється:

(5.11)

де х_Ме – нижня границя медіанного інтервалу;

Δ_Ме – довжина медіанного інтервалу;

f_Ме – частота медіанного інтервалу;

Σf/2 – півсума абсолютних частот ряду;

S_Мe-1 – сума частот інтервалів, що передують медіанному інтервалу.

20. Варіація – такі кількісні зміни досліджуваної ознаки в межах однорідної сукупності, що обумовлені впливом різних факторів. Розрізняють систематичну і випадкову варіацію.

21. Показники варіації (4.2-5) – узагальнюючі числові характеристики розсіювання набору елементів (одиниць статистичної сукупності); якщо набір складається з елементів x₁, x₂, …, x_N, то їх показники варіації можуть бути абсолютними, середніми та відносними.

22. Абсолютний показник варіації (R). Розмах варіації R (4.2) – це різниця між найбільшим і найменшим значеннями ознаки:

R = x_max – x_min. (5.12)

23. Середні показники варіації. Поширені середні показники варіації у варіаційних рядах: середнє лінійне абсолютне відхилення (СЛАВ) (4.3), дисперсія (4.4) та середнє квадратичне відхилення (СКВ) (4.5).

24. СЛАВ в дискретному ряду ( ) – це середньозважена міра лінійного абсолютного відхилення варіантів x_j дискретного ряду від середнього арифметичного значення ознаки Х в цьому ряду:

(5.13)

25. СЛАВ в інтервальному ряду ( ) – це середньозважена міра лінійного абсолютного відхилення серединних значень x_j´ ознаки X в інтервалах ряду від середнього арифметичного її значення в цьому ряду:

(5.14)

26. Дисперсія в дискретному ряду (D = σ²) – це середньозважена міра квадратичного відхилення варіантів x_j дискретного ряду від середнього арифметичного значення ознаки Х в цьому ряду:

(5.15)

27. Дисперсія в інтервальному ряду (D = σ²) – це середньозважена міра квадратичного відхилення серединних значень x_j´ ознаки X в інтервалах ряду від середнього арифметичного її значення в цьому ряду:

(5.16)

28. СКВ (σ) є коренем квадратним з дисперсії ознаки у варіаційному ряду:

(5.17)

29. Відносні показники варіації. Поширеними серед відносних показників варіації є коефіцієнт осциляції, відносне лінійне відхилення та коефіцієнт варіації.

30. Коефіцієнт осциляції (К_о) – коефіцієнт, який відображає у варіаційному ряду відносне розсіювання крайніх значень x_min і x_max ознаки Х навколо середнього арифметичного її значення , як відношення розмаху варіації до середнього арифметичного (може обчислюватись у відсотках, множенням К_о на 100%):

(5.18)

31. Відносне лінійне відхилення ( ) – коефіцієнт, який показує питому вагу середнього відхилення кожного значення x_j ознаки X вліво та вправо від її середнього арифметичного , як відношення середнього лінійного абсолютного відхилення до середнього арифметичного (може обчислюватись у відсотках, множенням на 100%):

(5.19)

Якщо > 32%, то має місце суттєва кількісна неоднорідність ознаки у досліджуваній сукупності.

32. Коефіцієнт варіації (υ) – найбільш поширений відносний показник варіації щодо оцінки типовості середніх величин. Він показує питому вагу середнього квадратичного відхилення кожного значення x_j ознаки X вліво та вправо від її середнього арифметичного , як відношення середнього квадратичного відхилення до середнього арифметичного (може обчислюватись у відсотках, множенням υ на 100%):

(5.20)

Якщо υ > 40%, то має місце суттєва варіація ознаки у досліджуваній сукупності.

33. Види дисперсії (елементи дисперсійного аналізу). Розрізняють наступні види дисперсій: загальну, міжгрупову, середнє внутрішніх групових дисперсій.

Дисперсійний аналіз застосовується для оцінки флуктуацій ознаки усередині кожної групи (вибірки) та відмінностей самих груп (вибірок).

34. Загальна дисперсія (σ_о²) для результативної ознаки характеризує варіацію, яка залежить від усіх факторів, що впливають на ознаку Х в межах досліджуваної сукупності:

(5.21)

де – загальне середнє у сукупності.

35. Міжгрупова дисперсія (δ²) для результативної ознаки відображає варіацію, яка виникає під впливом факторної ознаки, що покладена в основу групування, і характеризує коливання групових (частинних) середніх навколо загального середнього :

(5.22)

де l – номер окремої групи, f_l – її абсолютна частота.

По відношенню до факторної ознаки ця варіація є систематичною.

36. Середнє внутрішніх групових дисперсій ( ) – дисперсія, яка характеризує випадкову варіацію в кожній окремій групі:

(5.23)

де – внутрішня дисперсія l-групи .

Випадкова варіація має місце під впливом інших, неврахованих факторів, і не залежить від факторної ознаки.

37. Правило додавання дисперсій: загальна дисперсія дорівнює сумі значень міжгрупової дисперсії та середнього з внутрішніх групових дисперсій:

(5.24)

38. Коефіцієнт детермінації (η²) – коефіцієнт, який характеризує у загальній варіації питому вагу (відсоток) варіації, що обумовлена факторною ознакою:

(5.25)

Якщо η² > 50%, то факторну ознаку можна вважати основною, а решту ознак, вплив яких на результативну ознаку становить (1– η²), – другорядними.

39. Дисперсія альтернативної (якісної) ознаки (σ_ω²)– дисперсія, яка дорівнює добутку частки ω₁ одиниць, які наділені ознакою, і частки ω₀ = (1– ω₁) одиниць, не наділених нею:

σ_ω² = ((1 – ω₁)² ∙ ω₁ + (0 – ω₀) ² ∙ ω₀) : (ω₁ + ω₀) = ω₁ ∙ ω₀. (5.26)

Вона не може бути більшою за 0,25.

Контрольні питання:

1. Абсолютні величини: визначення, місце застосування в процесі статистичного дослідження, джерела даних, види абсолютних показників, порядок і правила їх подання.

2. Відносні величини: визначення, місце застосування в процесі статистичного дослідження, джерела даних, види відносних показників, порядок і правила їх подання.

3. Середні величини: визначення та загальна степенева форма середнього; види середніх.

4. Середнє арифметичне: визначення, властивості, види та способи розрахунку в дискретних й інтервальних рядах.

5. Середнє гармонічне, середнє квадратичне, середнє геометричне; умови застосування та способи розрахунку.

6. Середнє логарифмічне, середнє інтегральне, середнє хронологічне, середнє альтернативної ознаки; умови застосування та способи розрахунку.

7. Структурні середні: види та призначення; визначення моди в дискретному й інтервальному варіаційних рядах, порядок обчислення.

8. Структурні середні: види та призначення; визначення медіани в дискретному й інтервальному варіаційних рядах, порядок обчислення.

9. Варіація: визначення, види, класифікація показників варіації.

10. Розмах варіації та середнє лінійне (абсолютне) відхилення дискретної статистичної ознаки, зміст та порядок обчислення.

11. Розмах варіації та середнє лінійне (абсолютне) відхилення інтервальної статистичної ознаки, зміст та порядок обчислення.

12. Дисперсія та середнє квадратичне відхилення дискретної статистичної ознаки, зміст та порядок обчислення.

13. Дисперсія та середнє квадратичне відхилення інтервальної статистичної ознаки, зміст та порядок обчислення.

14. Властивості дисперсії й її види; правило додавання дисперсій.

15. Відносні показники варіації: види, порядок обчислення в дискретних й інтервальних варіаційних рядах.