Метод к-средних

Метод К-средних относится к группе так называемых эталонных методов кластерного анализа. Число кластеров К задастся пользователем. Процедура состоит в следующем. На первом шаге определяют К кластеров – эталонов (это могут быть, например, первые К объектов). Далее каждый объект присоединяется к ближайшему эталону. В качестве критерия используется минимальное расстояние внутри кластера относительно среднего. Как только объект включается в кластер, среднее пересчитывается. После пересчета эталона объекты снова распределяются по ближайшим кластерам и т.д. Процедура заканчивается при стабилизации процесса, т.е. при стабилизации центров тяжести.

Пример 2. Провести классификацию п = 10 объектов, каждый из которых характеризуется тремя признаками: х, у и z (табл.1.3).

Таблица 1.3

Данные для примера 2

x	y	z
0,252	2,100	2,600
0,322	2,700	2,600
0,339	2,000	2,000
0,406	1,000	1,000
0,492	2,200	2,000
0,507	2,300	2,000
0,695	2,300	2,400
0,751	2,100	2,100
0,903	2,400	2,100
0,971	2,400	2,500

1. Визуализация данных (в трехмерном случае).

В меню «Графика» выберите «3М XYZ графики». В выпадающем меню выберите команду «Диаграммы рассеяния», в появившемся окне нажмите на кнопку «Переменные» и задайте X, Y, Z (рис.1.14).

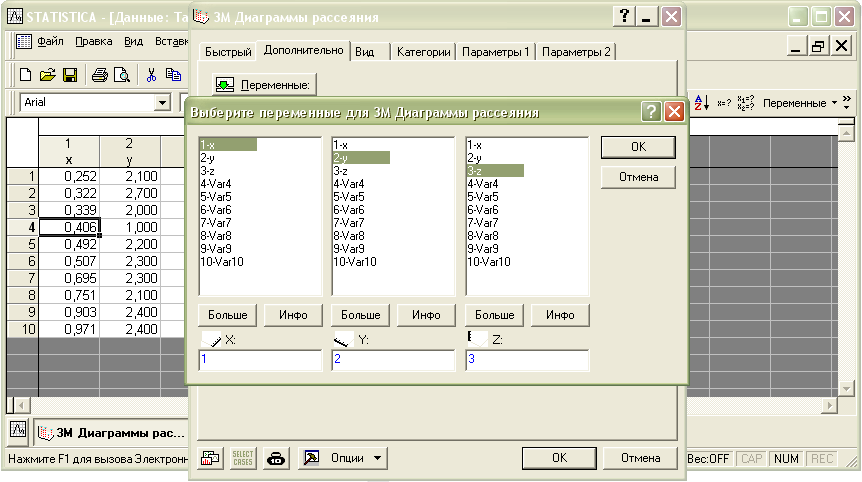
Рис.1.14. Выбор переменных для 3М диаграммы рассеяния

Затем нажмите на кнопку «Параметры 1» и включите «Имена наблюдений», нажмите ОК.

На экране появится диаграмма рассеяния для исходных данных (рис.1.15). На диаграмме видно, что объекты образуют три кластера.

Рис.1.15. 3М диаграмма рассеяния

2. Проведем кластерный анализ с помощью метода К-средних. Нажмите кнопку «Анализ» на панели инструментов, в выпадающем меню выберете модуль «Многомерный разведочный анализ», а затем «Кластерный анализ», где в методах кластеризации выберите опцию: «Kластеризация методом К-средних». В новом окне выполните следующие настройки:

а) нажмите на кнопку «Переменные» и введите переменные x, y, z;

б) во вкладке «Дополнительно» в разделе «Объекты» выберите «Переменные (строки)»;

в) в разделе «Число кластеров» задайте число кластеров, равное трем;

г) задайте число итераций;

д) выберете один из трех методов для начального определения центров кластеров (эталонов): либо выбираются первые К-объектов, либо выбираются объекты наиболее отстоящие друг от друга, либо отстоящие друг от друга на одинаковом расстоянии.

После выбора установок нажмите ОК.

3. Результаты кластеризации.

a. Дисперсионный анализ – результаты дисперсионного анализа по каждому признаку x, y, z (рис.1.16): выводятся суммы квадратов отклонения объектов от центров кластеров (Внутри SS) и суммы квадратов отклонений между центрами кластеров (Между SS), значения К-статистики и уровни значимости р.

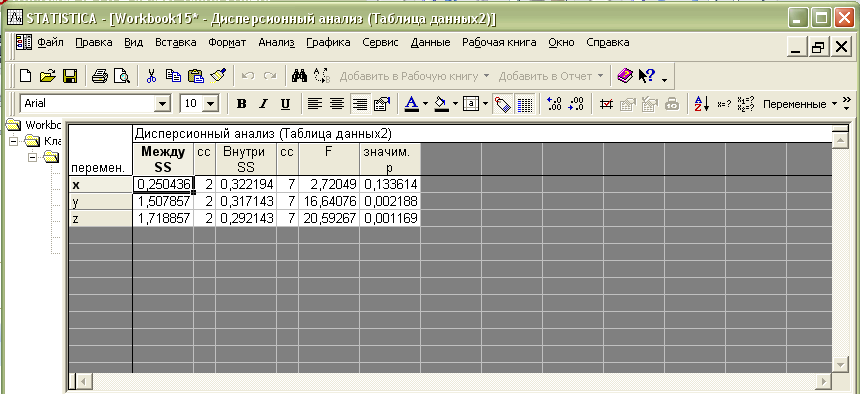
Рис.1.16. Результаты дисперсионного анализа

В данном примере уровни значимости равны: 0,1336; 0,0022; 0,0012, т.е. по x, y, z гипотезы о равенстве средних для центров кластеров отклоняются на уровне значимости а > 0,1336.

б. Выводятся координаты центров и матрицы расстояний между центрами (рис.1.17).

в. График распределения центров кластеров (рис.1.18):

Рис.1.17. Координаты центров и матрицы расстояний между центрами

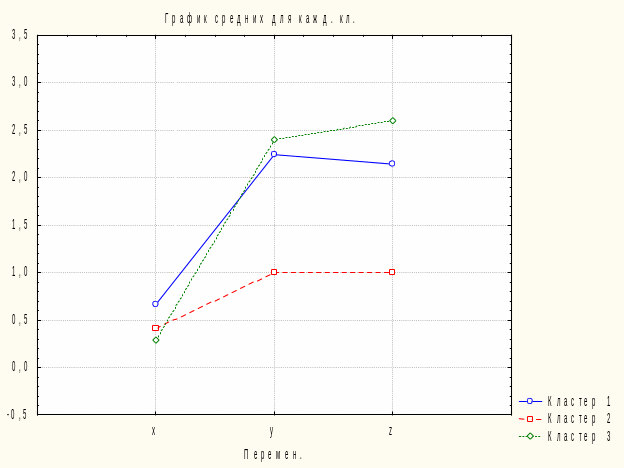
Рис.1.18. График распределения центров кластеров

г. Статистики для каждого кластера по координатам x, y, z средние центров, стандартные отклонения и дисперсии.

д. Номера объектов, входящих в каждый кластер и расстояния объектов до центра каждого кластера.

В данном примере объекты распределились следующим образом: кластер I: {6, 7, 8. 9, 10}; кластер 2: {4}; кластер 3: {1, 2, 3, 5}.