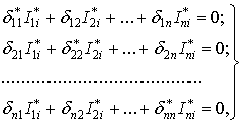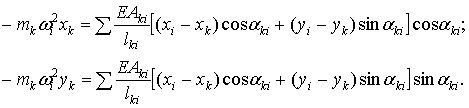4.6 Колебания плоских ферм

Если учитывать распределенные массы стержней фермы, то она является системой с бесконечным числом степеней свободы. Можно принять расчетную схему, в которой узловые соединения считаются шарнирными, а массы стержней фермы и нагрузки — распределенными по узлам. При этом ферма превращается в систему с конечным числом степеней свободы, а расчет считается «точным», хотя очевидно, что в силу принятых допущений он таковым не является.

Иногда вводятся дополнительные предпосылки: пренебрежение малыми массами, некоторыми перемещениями и т.д.

В такой постановке задачи канонические уравнения, описывающие свободные колебания фермы, имеют вид

(4.14)

где

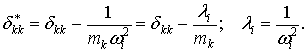
Некоторые массы в узлах фермы могут иметь два независимых перемещения, такая масса будет создавать две силы инерции, поэтому нужно использовать нумерацию перемещений или сил инерции, а не масс.

Уравнения (4.14) — однородные, поэтому имеют ненулевое решение только при условии равенства нулю определителя системы. Раскрывая этот определитель, можно получить частотное уравнение.

Для изучения симметричных и кососимметричных колебаний в фермах используется способ парных перемещений. При этом канонические уравнения перемещений имеют такой вид, что нет необходимости определять перемещения вида  . Не вдаваясь в промежуточные преобразования, приведем эти уравнения в их развернутом виде:

(4.15)

Уравнения (4.15), как и уравнения (4.14) — однородные, поэтому, приравнивая определитель нулю, можно получить частотное уравнение.

Для массы с двумя степенями свободы записываются два уравнения (4.15), а для массы с одной степенью свободы — одно из них.

Для балочных ферм с параллельными или близкими к ним поясами приемлемую точность дает метод определения собственных частот фермы через заменяющую ее балку.

Сказанное выше свидетельствует о том, что аналитический расчет ферм на свободные колебания представляет собой если и не очень сложную, то достаточно трудоемкую задачу.

Рассмотрим порядок расчета ферм в программе ANSYS. Определим собственные частоты и формы колебаний фермы с нагрузкой, приложенной в узлах верхнего пояса (рис.4.18).

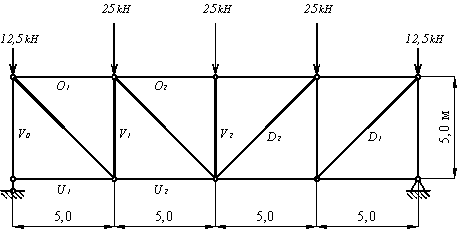
Рис.4.18

В результате аналитического расчета, выполненного в [4], первая частота собственных колебаний составила

Порядок решения задачи в программе ANSYS:

1. Задаем геометрические параметры фермы.

Utility Menu > Parameters > Scalar Parameters…

В поле Selection вводим параметры, которые будут использоваться в расчете. После ввода каждой константы нажимаем Accept.

O1 = 0.015 !Площади поперечных сечений стержней О1, О2,…,V2

O2 = 0.020

U1 = 0.005

U2 = 0.005

D1 = 0.010

D2 = 0.010

V0 = 0.020

V1 = 0.015

V2 = 0.015

F1 = 12500 !Нагрузка

F2 = 25000 !Нагрузка

L = 5 !Длина панели и высота фермы

2. Строим точки, определяющие конфигурацию фермы.

Main Menu>  Preprocessor> Modeling > Create > Keypoints > In Active CS

В поле NPT Keypoint number вводим номер точки, в полях X, Y, Z Location in active CS — ее координаты:

N       1        2        3        4        5        6        7        8       9        10

x        0        L     L*2    L*3    L*4    L*4   L*3    L*2    L         0

y        0        0        0        0        0        L       L       L       L         L

z        0        0        0        0        0        0        0        0       0         0

3. Соединяем точки линиями.

Main Menu>Preprocessor>Modeling>Create>Lines>Lines>Straight Line

Соединяем точки в соответствии со схемой (рис.4.18).

4. Задаем тип элемента.

Main Menu>Preprocessor>Element Type>Add/Edit/Delete>Add…

В левом поле окна выбираем Link, в правом — 2D spar 1. ОК. Close.

5. Задаем реальные константы элемента.

Main Menu>Preprocessor>Real Constants>Add/Edit/Delete>Add…>OK

В появившемся окне задаем реальные константы для стержня О1. В поле Real Constant Set No вводим номер реальной константы — 1, в полеCross-sectional area AREA вводим площадь сечения — О1 (рис.4.19). Apply.

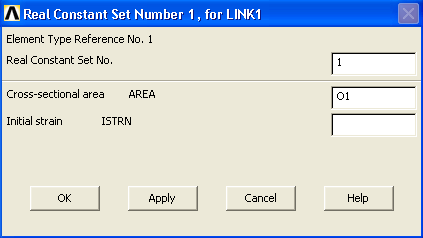
Рис.4.19

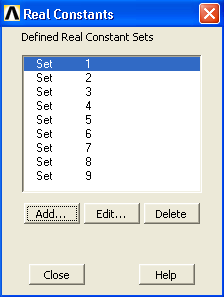
Рис.4.20

Аналогичным образом вводим номера реальных констант и площади поперечных сечений остальных стержней (Set 2 — O2,  Set 3 — U1, Set 4 — U2, Set 5 — D1, Set 6 — D2, Set 7 — V0, Set 8 — V1, Set 9 — V2).

В конечном итоге окно Real Constants будет содержать девять наборов реальных констант — по количеству различных стержней фермы (рис.4.20).

Закрываем окно нажатием Close.

6. Задаем свойства материала.

Main Menu > Preprocessor > Material Props > Material Models

В появившемся окне выбираем:

Structural > Linear > Elastic > Isotropic

Вводим модуль упругости EХ и коэффициент Пуассона PRXY:

EX: 2.2e11

PRXY: 0.3

Выбираем Density. В открывшемся окне в поле DENS вводим плотность материала — 7800. ОК.

7. Присваиваем стержням соответствующие атрибуты.

Main Menu > Preprocessor > Meshing > Mesh Attributes > Picked Lines

Выделяем стержни О1. ОК. В окне Line Attributes в выпадающем меню REAL Real constant set number выбираем: 1. Apply. Аналогичным образом присваиваем атрибуты всем остальным стержням.

8. Задаем количество разбиений на линии.

Main Menu > Preprocessor > Meshing > Mesh Tool

В появившемся окне нажимаем Set рядом с Lines, в окне Element Size on Picked... нажимаем Pick All. ОК. В поле NDIV No, of element divisionsуказываем число разбиений на линии — 1. OK.

9. Строим конечно-элементную сетку.

Main Menu > Preprocessor > Meshing > Mesh Tool

Нажимаем Mesh, в окне Mesh Lines — Pick All.

Пронумеруем точки:

Utilily Menu > PlotCtrls > Numbering...

В поле KP Keypoint numbers ставим переключатель в положение On. ОК.

Прорисуем линии:

Utilily Menu > Plot > Lines

10. Задаем условия закрепления.

Main Menu>Solution>Define Loads>Apply > Structural > Displacement > On Keypoints

Выделяем точку 1. ОК. В окне Apply U, ROT on KPs выбираем UY. Apply. Выделяем точку 5. ОК. В окне Apply U, ROT on KPs выбираем UX, UY.OK.

11. Прикладываем сосредоточенную нагрузку.

Main Menu > Solution > Define Loads > Apply > Structural > Force/Moment > On Keypoints

Выделяем точки 6 и 10. ОК. В выпадающем меню Lab Direction of force/mom выбираем FY, в поле VALUE Force/moment value вводим величинунагрузки: -F1. Apply. Выделяем узлы 7, 8 и 9. ОК. В окне Apply F/M on KPs выбираем FY и вводим величину нагрузки: -F2. ОК.

Выделяем всю конструкцию:

Utility Menu > Select > Everything

12. Переходим в командный режим.

/SOLU ! Вход в процессор решения

ANTYPE, 2 ! Анализ на собственные частоты

MODOPT, SUBSP, 4 ! Спецификация метода решения и количество частот

EQSLV, FRONT ! Тип решателя

MXPAND, 4,,,0 ! Записывать решение пяти собственных форм

SOLVE ! Запуск на решение

FINISH

/POST 1 ! Вход в постпроцессор

SET, FIRST ! Просчитать первый ряд расчетных значений

PLDISP,1 ! Вывести первую форму колебаний

SET,NEXT ! Следующая форма колебаний

PLDISP,1

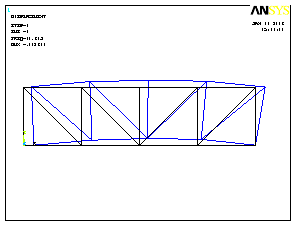
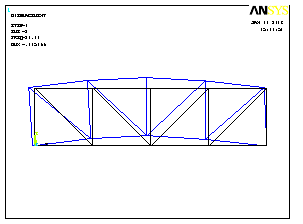
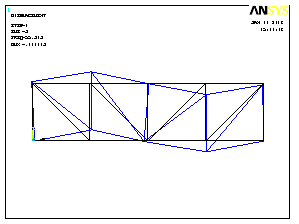
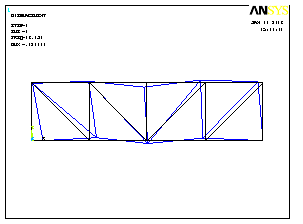
Формы колебаний показаны на рис.4.21.

1 форма колебаний	2 форма колебаний
3 форма колебаний	4 форма колебаний

Рис.4.21

Листинг со значениями собственных частот выводится с помощью пункта меню:

Main Menu > General Postproc > Results Summary

*****  INDEX OF DATA SETS ON RESULTS FILE  *****

   SET   TIME/FREQ    LOAD STEP   SUBSTEP  CUMULATIVE

     1            17.673                  1                     1                     1

     2            24.410                  1                     2                     2

     3            55.373                  1                     3                     3

     4            76.131                  1                     4                     4