4.5 Собственные колебания арок

Арка (шарнирная или безшарнирная, с затяжкой или без нее) является системой с бесконечным числом степеней свободы. Точный метод аналитического расчета арок на колебания на сегодняшний день отсутствует, и используются приближенные или численные методы.

Приближенные методы расчета основаны на замене арки системой с конечным числом степеней свободы. При этом арка делится на участки; сосредоточенные массы (при их наличии) и непрерывно распределенная масса заменяются одной сосредоточенной, расположенной в центре тяжести заменяемых масс, или на границах смежных участков арки (рис.4.12).

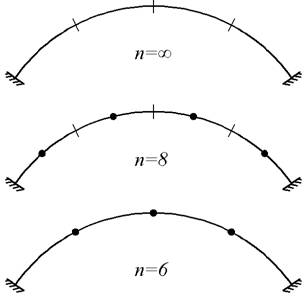
Рис.4.12

Число степеней свободы образованной системы равно удвоенному числу промежуточных масс или на две степени свободы (что соответствует одной массе) ниже (рис.4.12).

Последующие упрощения достигаются заменой арки ломаным брусом (рамой), которая также может проводиться разными способами: прямые брусья могут располагаться между границами участков или между массами (рис.4.13).

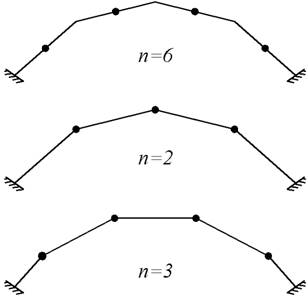
Рис.4.13

При этом дополнительно можно принять, что деформации растяжения-сжатия брусьев рамы отсутствуют, что приводит к дополнительному снижению числа степеней свободы образованной системы.

Далее используются точные или приближенные методы расчета стержневых систем с конечным числом степеней свободы.

Как и при решении многих задач механики деформируемого твердого тела, весьма эффективным для расчета арок на колебания является метод граничных элементов. Одним из авторов этой книги получено дифференциальное уравнение свободных колебаний круговой арки в виде

.

(4.12)

где  — окружная компонента перемещения.

Соответствующее характеристическое уравнение:

  

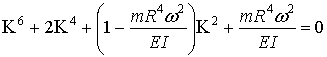
или

(4.13)

где      ,           .

Решение уравнения (4.12) будет зависеть от корней характеристического уравнения (4.13).  С математической точки зрения здесь возможны десять случаев корней.

Каждой группе корней уравнения при использовании метода граничных элементов соответствуют 36 ортонормированных фундаментальныхфункций; всего получено 360 фундаментальных функций задачи.

Следуя обычному алгоритму решения методом граничных элементов [3], можно определить все параметры вектора состояния арки при свободных колебаниях.

При расчете конкретной арочной системы параметр Z в (4.13) может быть вычислен с точностью до частоты собственных колебаний  . Поэтому для   нужно задавать интервал изменения, например,  (0, 1000) с^-1, после чего в процессе реализации программы расчета в MATLAB, DELPHI или какой-либо иной среде осуществляется автоматический переход к вычислению фундаментальных функций, соответствующих корням характеристического уравнения (4.13).

Программа, реализующая расчет арочной системы методом граничных элементов в соответствии с изложенной методикой, достаточно объемна, однако это связано с большим количеством арифметических операторов и логических разветвлений. В действительности затраты компьютерных ресурсов являются минимальными, так как приходится решать систему только двенадцати (!)  алгебраических уравнений, что существенно меньше, чем при использовании метода конечных элементов.

Поскольку более подробное изложение методики расчета арки на колебания выходит за рамки данной книги, то перейдем к расчету арки на свободные колебания в программе ANSYS. Определим первые пять частот и форм собственных колебаний круговой двухшарнирной арки (рис.4.14).

Рис.4.14

Вычисленная аналитически низшая частота колебаний такой арки при следующих исходных данных: радиус оси арки   половина центрального угла  , линейная плотность арки   интенсивность внешней радиальной нагрузки (гидростатическое давление)    жесткость   составила  .

Последовательность действий в программе выглядит так:

1.Задаем тип элемента и его опции.

Main Menu > Preprocessor > Element > Type > Add/Edit/Delete > Add…

В окне Library of Element Types выбираем Beam 2D elastic 3. ОК. В окне Element Types нажимаем кнопку Оptions… и в выпадающем меню Оutputat extra intermed pts K9 выбираем 9 intermed pts. ОК. Сlose.

2.Задаем реальные константы элементов.

Main Menu > Preprocessor > Real Constants > Add/Еdit/Delete > Add…

В окне Element Types for Real Co… выбираем Type 1 BEAM3. ОК. В появившемся окне необходимо ввести:

AREA: 3.14*2.269**2/4 !площадь поперечного сечения

IZZ: 3.14*2.269**4/64 !момент инерции сечения

HEIGHT: 2.269 !высота сечения      

ADDMAS: 63800 !линейная плотность стали    ОК. Close.

3.Задаем свойства материала для элемента BEAM3.

Main Menu > Preprocessor > Material Props > Material Models

 В правом поле появившегося окна выбираем:

Structural > Linear > Elastic > Isotropic

В полях EX и PRXY вводим соответственно модуль упругости и коэффициент Пуассона:

EX: 2e11

PRXY: 0.3    ОК.

Переходим в цилиндрическую систему координат:

Utility Menu > WorkPlane > Change Active CS to > Global Cylindrical

4.Задаем основные узлы.

Переходим в командный режим ANSYS Command Promt:

n, 1, 170, 90+36

n, 21, 170, 90-36

fill, 1, 21, 19 !Задаем промежуточные узлы

5.Определяем элемент BEAM3 на каждом участке.

*do, i, 1, 20

e, i, i+1

*enddo

6.Задаем условия закрепления.

Main Menu>Solution>Define Loads > Apply > Structural > Displacement > On Nodes

Выбираем узлы 1 и 21. ОК. В окне  Apply U, ROT on Nodes выбираем All DOF. ОК.

7.Прикладываем радиальную нагрузку.

Main Menu>Solution>Define Loads>Apply>Structural>Pressure>On Beams

Нажимаем Pick All. В окне Apply PRES on Beams в полях VALI, VALJ вводим величину нагрузки — 63800. ОК (рис.4.15).

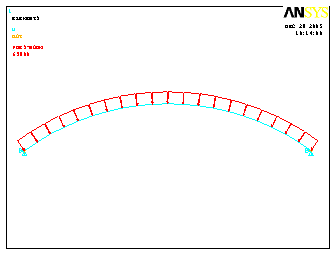
Рис.4.15

Выделяем всю конструкцию.

Utility Menu >Select > Everything

8.Переходим в командный режим ANSYS Command Promt.

/SOLU

ANTYPE, 2 !анализ на собственные частоты

MODOPT, SUBSP, 5 !спецификация метода решения

EQSLV, FRONT !тип решения

MXPAND,5,,,0 !записывать решение пяти собственных частот

SOLVE !запуск на решение

9. Чтение результатов.

9.1. Листинг со значениями собственных частот доступен через следующий пункт меню (рис.4.16):

Main Menu > General Postproc > Result Summary

*****  INDEX OF DATA SETS ON RESULTS FILE  ***** SET   TIME/FREQ    LOAD STEP   SUBSTEP  CUMULATIVE 1          0.40724                    1                     1                       1 2          0.75759                    1                     2                       2 3            1.3758                    1                     3                       3 4            1.9746                    1                     4                       4 5            2.9017                    1                     5                       5

Рис.4.16

9.2. Графический вывод форм колебаний.

/POST 1

SET, FIRST !первая форма колебаний

PLDISP, 1

SET, NEXT !следующие формы колебаний

PLDISP, 1

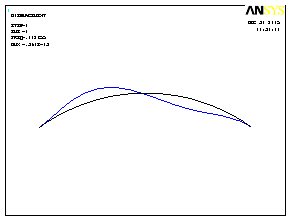
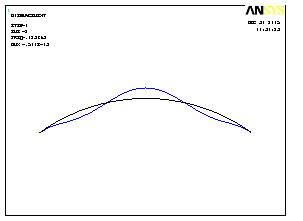
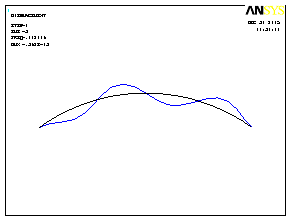
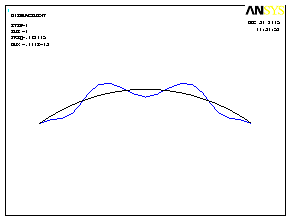
Первые четыре формы колебаний показаны на рис.4.17.

1 форма колебаний	2 форма колебаний
3 форма колебаний	4 форма колебаний

Рис.4.17
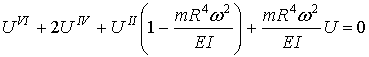