Перевод чисел из одной системы счисления в другую систему счисления

П еревод дробной части числа

0,62₁₀= 0,100111₂

101011,01011₂=1*2⁵+0*2⁴+1*2³+0*2²+1*2¹+1*2⁰+0*^-1+1*2^-2+0*2^-3+1*2^-4+1*2^-5

Пеpевод из двоичной системы исчисления в 16-тиричную осуществляется по таблице для каждых 4-х двоичных единиц:

0000=0 0001=1 0010=2 0011=3

0100=4 0101=5 0110=6 0111=7

1000=8 1001=9 1010=A 1011=B

1100=C 1101=D 1110=E 1111=F

Например:

число 111010110 = 0001'1101'0110 = 1D6

Арифметические операции в двоичной системе счисления

1. Что такое двоичная, десятичная и, вообще, позиционная система счисления.

Это такая система, в которой значение каждой цифры в записи числа зависит от её разряда (позиции).

Например, в привычной для нас десятичной системе счисления число 777 = 7 сотен + 7 десятков + 7 единиц. Т.е. одна и та же цифра 7 означает разные количества, — или сотни, или десятки, или единицы, —  в зависимости от того, какой разряд (позиция).

Далее, в разряде единиц могут находиться следующие цифры: 0,1,2,3,4,5,6,7,8,9. Они обозначают соответствующие количества (числа). Следующее число — 10. При записи этого числа произошло переполнение разряда единиц. В результате в разряде единиц появился нуль, но зато в разряде десятков единица. Аналогично происходит переполнение всех прочих разрядов.

В двоичной системе переполнение разрядов происходит уже при двух, в троичной системе при трёх и т.п.

2. Сложение в двоичной системе счисления

Таблица сложения в двоичной системе очень проста:

0+0=0,    0+1=1,   1+0=1,     1+1=10.

П редставим последнее равенство на шахматной доске: 0 — шашки нет, 1 — шашка есть.

Две шашки вызывают переполнение разряда.

Отсюда понятно правило сложения:

— если в вертикальном ряду есть две шашки, то их снимаем с доски, вместо них выставляем одну шашку в левом соседнем ряду.

— эта операция, если необходимо, повторяется; она сама собой прекратится, когда в ряду останется только одна шашка или не останется ни одной шашки.      

При решении конкретных задач правило сложения применяется многократно до тех пор, пока не получится окончательный результат, который спускаем в самую нижнюю строку, расположенную под линией,  —  в строку результатов.

Пример на сложение: 7+5+9=21.

3. Вычитание в двоичной системе счисления

В качестве примера рассмотрим 9-3=6:

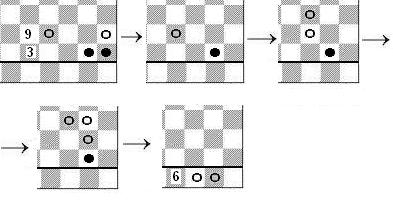
В первом разряде вычитание производится просто: 1(белая шашка)-1(чёрная шашка)=0.

Во втором разряде приходится из нуля вычитать единицу, поэтому "занимаем" в старших разрядах. — Шашку старшего разряда убираем, но зато вместо неё ставим две шашки в соседнем младшем разряде.

В нашем примере мы воспользовались этим правилом дважды, наконец, результат снесли в самую нижнюю строку результатов.

4. Умножение и деление в двоичной системе счисления

Сначала полезно несколько раз убедиться в том, что в результате удвоения числа, т.е. сложения его с самим собой, число без изменения перемещается на один разряд влево. Иначе говоря, к записи числа справа приписывается один нуль.

Например,

5х2 = 10 в двоичной системе:

101х10=101+101=1010.

Если умножить на четыре, т.е. два раза по два, то справа приписывается два нуля

5х2х2 = 10х2=20 в двоичной системе:

101х10х10=1010+1010=10100.

И т.д.

Операции умножения и деления основаны на таблице умножения, которая в двоичной системе выглядит точно так же, как соответствующая часть таблицы умножения в десятичной системе:

0х0=0,  0х1=0, 1х0=0, 1х1=1.

Отсюда понятно, что умножение столбиком и деление уголком выполняется точно так же, как в десятичной системе, с единственным отличием, — сложение и вычитание, там, где это требуется,  выполняются по правилам двоичной системы, т.е. по правилам, рассмотренным выше.

Поэтому нет необходимости рассматривать операции умножения и деления подробно. Ниже приводятся лишь один пример на умножение, 7х5=35, и один пример на деление, 20:3=6(2 в остатке):

Обратим внимание, что во всех операциях, кроме деления, имелась полная определённость с разрядами, поэтому нуль изображался отсутствием шашки.

При операции деления такая определённость пропала, поэтому нуль необходимо изображать явно. Можно, например, шашку перевернуть, как будто это дамка, и договориться, что так будем изображать нуль.

Вот и всё. Все главные особенности арифметических операций уже освоены. Теперь, для того, чтобы научиться вычислениям в десятичной системе, достаточно лишь выучить десятичные таблицы сложения и умножения.