Ответы на вопросы по математике, экзамен.

№1

Определители II и III порядка. Их вычисление.

Выражение а1в2-а2в1 называется определителем второго порядка и обозначается символом...

Числа а1в1;а2в2- называются элементами определителя. а1 и в2- главная диагональ, а2 и в1- побочная диагональ…

Определителем третьего порядка, составленным из чисел: а1,в1,с1,а2,в2,с2,а3,в3,с3- называется число, определяемое равенством.

1 сп.

2 сп.

№2

Действия над матрицами (сложение, вычитание, умножение на число).

Опр. Совокупность чисел, расположенных в виде таблицы из m- строк и n-столбцов, называют матрицей размером.

Опр. Если количество строк равно количеству столбцов, то матрица называется квадратной

Опр. Если количество строк и столбцов не совпадают, то матрица называется прямоугольной.

Опр. Если матрица состоит из одного столбца, то она называется матрицей- столбцом.

Опр. Если матрица состоит из одной строки, то матрица называется строкой матрицей.

Опр. Матрица называется нулевой, если все её элементы равны нулю.

Опр. Матрица называется диагональной , если все её элементы, кроме элементов стоящи на главной диагонали равны нулю.

Опр. Матрица называется единичной, если она диагональная, и все её элементы состоящие на главной диагонали равны единице.

Опр. Две матрицы А и В называются равными, если их соответствующие элементы равны между собой.

Опр. Две матрицы называются противоположными, если их элементы отличаются только знаком.

Действия над матрицами.

А=

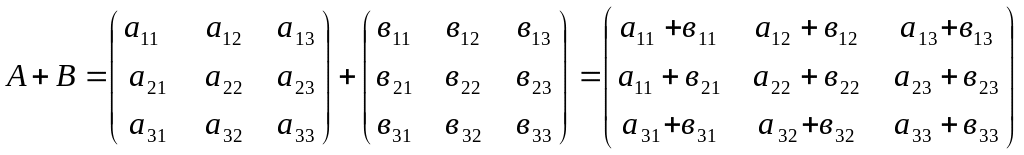
2) Вычитание:

3. Умножение матрицы на число #0

№3

Умножение матриц.

(Возможно только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы)

Пример:

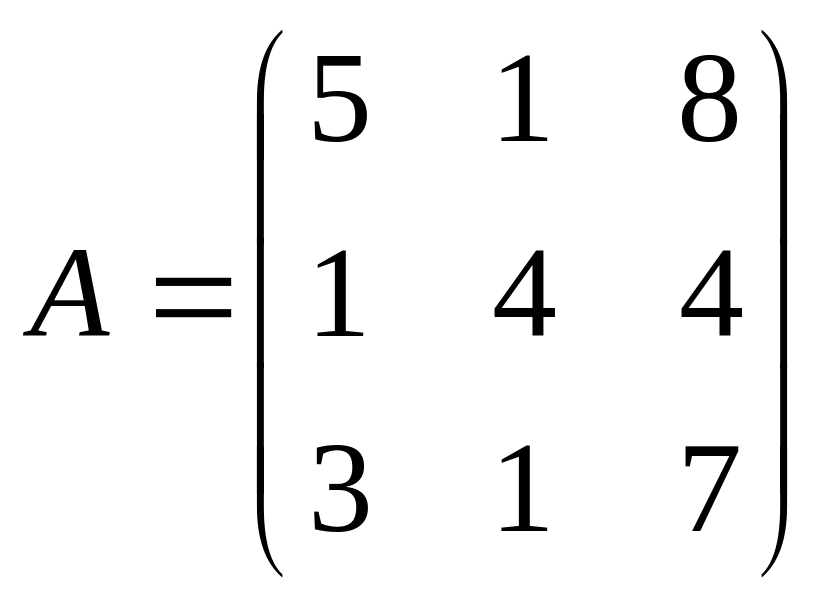
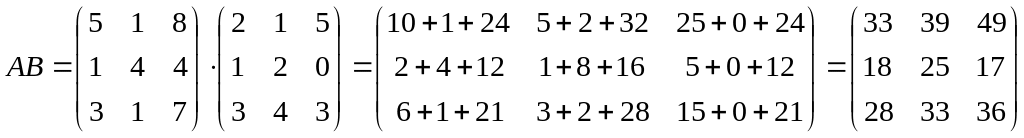
№4

Обратная матрица и её нахождение.

Опр. Матрица А^-1 называется обратной для матрицы А, если выполняется условие

- единичная матрица

Обратную матрицу обозначают А^-1

Утверждение: Для данной матрицы А существует обратная матрица, если данная матрица квадратная и ее определитель не равен нулю.

где А_ij – алгебраическое дополнение матрицы А, причем знак А_ij будет равен (-1)^i+j

Пусть

№5

Матричный метод решения систем линейных уравнений.

Решение:

Составим матрицы:

№6

Решение систем уравнений по правилу Крамера.

…

Если определитель системы А=0, то система является либо несовместной, либо неопределённой. В последнем случае система сводится к одному уравнению, а другое является следствием этого уравнения.

… условия несовместности

… условия неопределённости.

Пример.

№7

Решение системы линейных уравнений методом Гаусса.

Для решение систем уравнений методом гаусса необходимо свести данную систему к треугольной.

а1х+в1у+с1z=d1

b2y+c2z=d2

c3z=d3

Для упрощения вычислений оперируют только с коэффициентами при неизвестных, составляя матрицу вида.

…

Преобразования производятся по следующим правилам.

1. можно менять строки местами.

2. Можно умножать или делить строку на любое число неравное нулю.

3. Можно складывать и вычитать строки между собой.

…

№8

Первообразная. Неопределённый интеграл и его свойства.

Функция y=F(x) называется первообразной для функции f(x) если y=F(x)’=f(x).

Правила вычисления первообразной.

Первообразная сумма равна сумме первообразных. Если первообразная умножается на число, то число выносится за знак первообразной.

Первообразная для функции y=f(x)малое, то первообразная функция будет равняться 1/k*F(fx+m).

Интегралы бывают определённые и неопределённые, вычисления неопределённого интеграла сводится к вычислению первообразных различными методиками (подстановка, интегрирование по частям).

Если F(x)- какая-либо первообразная функция для f(x), то выражениеF(x)+C, где C- произвольная постоянная, называется неопределённым интегралом от функции f(x) и обозначается символом ∫ f(x) dx.

При этом функция f(x) называется подынтегральной функцией, а выражение f(x) dx называется подынтегральным выражением, знак ∫ называется знаком интеграла.

Согласно определению неопределённого интеграла, можно записать ∫f(x)dx=F(x)+C.

Операция нахождения первообразной по данной функции называется интегрированием.

Свойства.

1.Производная неопределённого интеграла равна подынтегральной функции, а дифференциал неопределённого интеграла равен подынтегральному выражению:

(∫f(x)dx)’=f(x)

d∫f(x)dx=f(x)dx.

Эти свойства непосредственно вытекают из определения неопределённого интеграла.

2. Неопределённый интеграл от дифференциала функции равен сумме этой функции и произвольной постоянной:

∫ dF(x)=F(x)+C

Для доказательства воспользуемся определением неопределённого интеграла:

∫f(x)dx=F(x)+C, но

dF(x)= f(x)dx, f(x)=F’(x), следовательно,

∫dF(x)=F(x)+C.

3. Постоянный множитель можно выносить за знак неопределённого интеграла:

∫ af(x) dx=a ∫ f(x)dx, a≠0.

4. Интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от этих функций, то есть ∫ (f₁(x)- f₂(x)+ f₃(x))dx= ∫f₁(x)dx-∫f₂(x)dx+∫f₃(x)dx.

№9

Нахождение определённого интеграла методом подстановки.

№10

Определённый интеграл и его свойства.

№11

Понятие предела функции в точке. Свойства пределов.

№12

Исследование на монотонность с помощью производной. Точки экстремума функции.

Монотонность- это промежутки возрастания или убывания функции.

Функция возрастает на промежутке (а:в) если производная на этом промежутке положительная.

Функция убывает на промежутке (а:в) если производная на этом промежутке отрицательная.

Точки экстремума- это точки минимума и максимума.

1)максимальная точка.

Точка х₀ называется точкой max если существует окрестность точки х₀ что для всех х из этой окрестности будет выполняться неравенство y(x₀)>y(x)

α- угол между касательной и положительным направлением оси ОХ

касательная || оси ОХ=> α=0⁰

y’=tgα tgα=0=>y(x₀)=0

если при переходе через точку слева на право производная функция меняет знак с «+» на «-» то это точка max.

2)минимальная точка.

Точка х₀ называется точкой min если существует окрестность в точке х₀, что для всех х из этой окрестности будет выполняться неравенство y(x₀)<y(x).

х₀- точка min

касательная || оси ОХ =>α=0⁰

y’= tgα tgα=0=>y’(x₀)=0

если при переходе через точку слева на право производная функция меняет знак с «-» на «+» то эта точка min.

Вывод: в точках экстремума первая производная функции равна 0.

№13

Выпуклость и вогнутость графика функции. Точки перегиба.

1) выпуклый.

График называется выпуклым если он расположен ниже касательных.

В тех промежутках где вторая производная функция отрицательная, график выпуклый.

2)график называется вогнутым если он расположен выше касательных.

В тех промежутках где вторая производная функции положительная график вогнутый.

3)точка перегиба.

Точка определяющая выпуклость от вогнутости называется точкой перегиба.

В точках перегиба вторая производная функции равна 0.

Точки перегиба.

Точками графика функции y=f(x) разделяющая промежутки выпуклости противоположных направлений этого графика называется точкой перегиба.

Точками перегиба могут служить только, критические точки, принадлежащие области определения функции y=f(x) в которых вторая производная f”(x) обращается в нуль или терпит разрыв.

Если при переходе через критическую точку Хо вторая производная f”(x) меняет знак, то график функции имеет точку перегиба (Хо; f’(Xo).

№14

Схема исследования функции. Показать на примере.

1. f’(x)

2. f’(x)=0

3. .

4. Вывод: а) функция возрастает если производная положительная

б) функция убывает если производная отрицательная

в) точка экстремума является min если производная меняет знак с – на +

г) точка экстремума является max если производная меняет знак с + на –

д) точка не является экстремумом если производная не меняет знак.

5) для нахождения наибольшего и наименьшего значения на отрезке, находим значение функций в концах отрезков и в критических точках в нутрии данного отрезка.

6) для нахождения выпуклости и вогнутости находим вторую производную f”(x)

7) f”(x)=0

8) если вторая производная положительная то функция выпукла вниз. Если вторая производная отрицательная то функция выпукла вверх.

Пример:

.

.

.

.

.

Вывод:

а) функция возрастает (-∞;-2)U(1;+∞)

б) функция убывает (-2;1)

в) точка х=-2 будет являться max, точка х=1 min.

г) наименьшее значение на отрезке [-3;6] f(-1)=4.5/6, наибольшее значение на отрезке f(6)=84

д) функция выпукла вверх (-∞;-1/2), выпукла вниз (-1/2; +∞)

№15

Наибольшее и наименьшее значение функции на промежутке .

№16

Вычисление площади криволинейной трапеции.

Фигура ограниченная кривой (прямой) y=f(x) прямыми у=0, х=а, х=b- называются криволинейной трапецией.

…

№17

Нахождение пути с помощью определённого интеграла.

Задан закон изменения скорости движения тел.

Ѵ=Ѵ_(t)

t€[a;b] S- путь или расстояние.

…

№18

Определение комплексного числа в алгебраической форме. Действия над комплексными числами в алгебраической форме.

Х²+1=0

Х²=-1

Х=±√-1

√-1=i

Комплексным числом i называется мнимой единицей, число а- вещественной частью, в- мнимой частью алгебраической формой комплексного числа a+bi.

I²=-1

I³=-i

I⁴=1

Комплексное число a-bi- называется сопряженным, комплексному числу z=a+bi и обозначается символом z.

Разностью u-v комплексных чисел u=a+bi и v=c+di называется такое комплексное число z=x+iy, которое в сумме с числом v даёт u, то есть z+v=u, x=a+I, y=b-a.

Частным u/v комплексных чисел u=a+bi и v=c+di (при v≠0), называется такое комплексное число z=x+yi, которое при умножении на v даёт u, то есть z=(c+di)=a+bi.

Для того чтобы сложить два комплексных числа, сначала складываются действительные части с действительными, а мнимые с мнимыми.

Z₁=a₁+b₁i, z₂=a₂+b₂i.

Z₁+z₂= a₁+b₁i+ a₂+b₂i=( a₁+ a₂)+( b₁+ b₂)i.

Вычитание можно выполнить аналогичным образом.

Z₁-z₂= a₁+b₁i-( a₂+b₂i)

Для того чтобы умножить комплексные числа необходимо перемножить скобки по обычному правилу умножения многочлена с обязательной заменой i.

Z₁*z₂= (a₁+b₁i)*( a₂+b₂i)= a₁*a₂+a₁b₂+a₂b₁i-b₁b₂=( a₁*a₂- b₁b₂)+( a₁b₂+a₂b₁)i.

Два комплексных числа необходимо умножить на сопряжённое знаменателю число…

Z1/z2=((a₁+b₁i)*( a₂-b₂i))/( a₂+b₂i)*( a₂-b₂i)=(как умноженbе)/ a₂²+b₂²=((a₁a₂- b₁b₂)+( a₁b₂+a₂b₁)i)/

/( a₂²+b₂²)=((a₁a₂- b₁b₂)/ (a₂²+b₂²))+((a₂b₁+a₁b₂)/( a₂²+b₂²)) i.

№19