1.3. Нахождение текущей стоимости (дисконтирование)

В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме FV, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды PV. В этом случае говорят, что сумма FV дисконтируется.

Величину PV, найденную дисконтированием наращенной величины FV, называют современной, текущей или приведенной величиной.

Текущая стоимость – это величина, обратная наращенной стоимости, т.е. дисконтирование и ставка дисконта противоположны понятиям «накопление» и «ставка процента».

Так как текущая стоимость является обратной величиной наращенной суммы, то она определяется по формуле:

,

где – дисконтный множитель. Он показывает текущую стоимость одной денежной единицы, которая должна быть получена в будущем.

ПРИМЕР 4. Определить современную (текущую) величину 20 тыс. руб., которые должны быть выплачены через 4 года. В течение этого периода на первоначальную сумму начисляются сложные проценты по ставке 8% годовых.

При начислении процентов m раз в году расчет текущей стоимости производится по формуле:

,

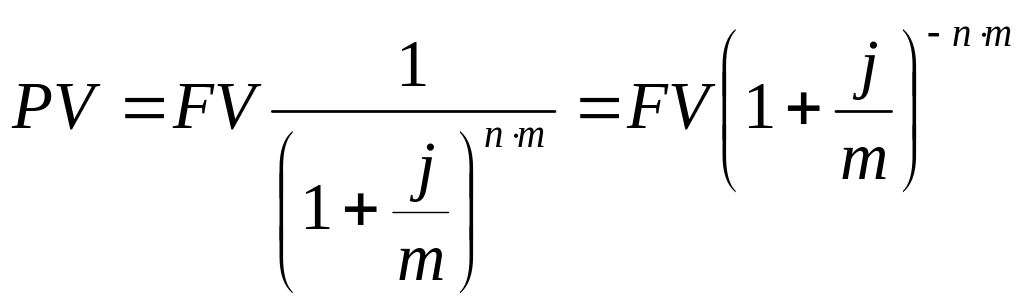1.4. Аннуитет. Наращенная сумма ренты

Оплата по заключенным сделкам может предусматривать как разовый платеж, так и ряд выплат, распределенных во времени, например, выплата арендной платы, выплаты за приобретенное имущество в рассрочку, инвестирование средств в различные программы и т.п. предусматривают платежи, производимые через определенные промежутки времени, т.е. образуется поток платежей.

Ряд последовательных фиксированных платежей, производимых через равные промежутки времени, называют финансовой рентой, или аннуитетом.

Обобщающими показателями ренты являются: наращенная сумма и современная (текущая, приведенная) величина.

Наращенная сумма ренты – это сумма всех членов потока платежей с начисленными на них процентами на конец срока, т.е. на дату последней выплаты. Наращенная сумма показывает, какую величину будет представлять капитал, вносимый через равные промежутки времени в течение всего срока ренты с начисленными процентами.

ПРИМЕР 5. Помещение сдается в аренду сроком на 5 лет. Арендные платежи в размере 10 тыс. руб. вносятся арендатором ежегодно в конце года в банк на счет владельца помещения. Банк на внесенные суммы начисляет проценты из расчета 20% годовых. Определить сумму, полученную владельцем помещения в конце срока аренды (табл. 3), при условии, что со счета деньги не изымались.

Таблица 3

Схема платежей, вносимых в течение всего срока аренды

Период взноса, год	1-й взнос	2-й взнос	3-й взнос	4-й взнос	5-й взнос
1-й 2-й 3-й 4-й 5-й Итого	10,0 10,0*1,2 10,0*1,22 10,0*1,23 10,0*1,24 10,0*1,2t-1	- 10,0 10,0*1,2 10,0*1,22 10,0*1,23 10,0*1,2t-2	- - 10,0 10,0*1,2 10,0*1,22 10,0*1,2t-3	- - - 10,0 10,0*1,2 10,0*1,2t-4	- - - - - 10,0

Сумму всех рентных платежей с начисленными на них процентами, можно определить по формуле суммы членов геометрической прогрессии:

,

где R – величина ежегодного платежа;

i – процентная ставка;

n – срок ренты.

Величина является коэффициентом наращения ренты, который называют также коэффициентом накопления денежной единицы за период.

По данным ранее рассмотренного примера рассчитаем наращенную сумму рентных платежей:

Некоторые ренты реализуются сразу после заключения контракта, т.е. первый платеж производиться немедленно, а последующие платежи – через равные интервалы. Такие ренты (пренумерандо) также называются авансовыми, или причитающимися аннуитетами. Сумма членов такой ренты вычисляется по формуле:

.