2.2.3. Використання комплексних чисел для аналізу кіл синусоїдного струму.

Застосування комплексних чисел для розрахунків кіл синусоїдного струму дає можливість замінити диференційні рівняння, якими описуються процеси у цих колах, алгебраїчними рівняннями. Метод аналізу та розрахунку електричних кіл синусоїдного струму з використанням комплексних часто називають символічним або комплексним методом.

З курсу математики відомо, що синусоїдну функцію, зокрема обертовий вектор-орт (рис. 2.10), можна записати комплексним числом. Тому при розрахунках електричних кіл синусоїдного струму, замість геометричних дій з векторами, використовують більш зручні і точніші алгебраїчні дії з комплексними числами.

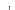
Рис. 2.10. До запису комплексного числа

Рис. 2.11. Лінійна вольт-амперна характеристика

Відомо, що комплексне число може бути записано у алгебраїчній, показниковій і тригонометричній формах, відповідно:

; ; ,

де a та b – відповідно, дійсна та уявна складові комплексного числа (проекції вектора на вісі, відповідно, дійсних та уявних чисел); А – модуль комплексного числа (довжина вектора);  – аргумент комплексного числа (кут нахилу вектора до вісі дійсних чисел); – уявне число; е – основа натурального логарифму.

Для переходу від однієї форми запису комплексного числа до іншої використовують співвідношення (рис. 2.10):

;; та .

Комплекс діючого значення електричної величини, що змінюється у часі за синусоїдою, виділяють крапкою над символом, який відображає цю величину. Наприклад: – комплекс діючого значення струму; – комплекс діючого значення напруги. Якщо електрична величина не є синусоїдною, то комплекс її значення виділяють рискою під символом, який відображає цю величину. Наприклад: Z – комплекс повного опору; S – комплекс повної потужності.

Додавати або віднімати комплексні числа зручніше коли вони надані у алгебраїчній формі запису:

;

Виконувати множення, або ділити – зручніше коли числа надані у показниковій формі:

;

Комплекси величини, які відрізняються тільки за знаком аргументу, називають спряженими комплексами. В електротехніці спряжений комплекс звичайно виділяють “зірочкою” над символом величини. Так, наприклад, якщо маємо

,

то спряжений комплекс буде:

Зазначимо, що при множенні комплексу величини на спряжений комплекс, в результаті одержимо квадрат модуля цієї величини –

.

2.2.4. Діюче і середнє значення синусоїдних величин.

Широке впровадження синусоїдного струму, обумовило необхідність пошуку простого та зручного способу розрахунку енергії, що віддає струм до зовнішнього кола. Використання для цього законів постійного струму і виконання дій у миттєвих значеннях змінного струму, призводить до громіздких розрахунків, що часто є недоцільним.

Звичайно, аналіз кіл синусоїдного струму можна було б проводити з використанням векторних діаграм, методика побудови яких у миттєвих значеннях синусоїдної величини розглянута вище. Але і при цьому є ускладнення. По-перше, геометричні дії, як правило, не забезпечують потрібної точності розрахунків. По-друге, для вимірювання миттєвих значень електричних величин потрібні складні і дорогі прилади – осцилографи. Вихід був знайдений на підставі властивостей енергії переходити з одного виду в інший.

Відомо, що при проходженні постійного струму І по провіднику з опором R, за час t у провіднику виділяється кількість теплоти (закон Джоуля-Ленца) – або .

Кількість теплоти протягом періоду T (t =Т), с, становитиме:

.

При цьому електрична потужність, як робота струму в одиницю часу, буде:

.

Оскільки при проходженні змінного струму в провіднику також виділяється теплота, то для оцінки цього ефекту у теорію змінного струму було введено поняття діюче або ефективне значення струму

Під діючим значенням змінного струму розуміють таке значення еквівалентного йому постійного струму, який проходячи в тому ж, що і змінний струм провіднику, за однаковий час виділяє у цьому провіднику таку ж кількість теплоти.

Кількість теплоти, яка виділиться при проходженні змінного струму - .

Отже, змінним струмом за той же час Т в тому ж опорі R буде виділено теплоти:

.

Тут для рішення використано, що , та те, що .

Врахувавши, що , находимо, що або , звідки маємо

.

З виразу , можна знайти, що , отже, миттєве значення змінного синусоїдного струму дорівнює діючому значення цього ж струму в момент часу

.

Отже. тепер можна сказати, що під діючим значенням змінного струму розуміють те із його миттєвих значень, яке, залишаючись незмінним у часі, виділить за один і той же час в одному і тому ж опорі таку ж кількість теплоти, як і струм, що змінюється за синусоїдою.

З порівняння: , знайдемо –

,

тобто, діюче значення синусоїдного струму є одночасно його середньоквадратичним значенням.

Використавши, що і що , знайдемо, що між максимальним миттєвим (амплітудним) і діючим значенням напруги та такими ж значенням ЕРС, існують такі ж залежності:

,

.

Відношення амплітудного значення змінної електричної величини до діючого значення цієї ж величини називають коефіцієнтом амплітуди. При синусоїдному законі зміни струму (ЕРС, напруги) коефіцієнт амплітуди буде: k_а = I_m/I = 1,41.

Поняття середнє значення змінної електричної величини використовують при аналізі роботи перетворювачів, випрямлячів, вимірювальних приладів випрямляючої системи та у ряді інших випадків.

В загальному випадку, при відомому законі зміни миттєвих значень будь-якої змінної величини, наприклад струму i, середнє значення I_сp, цієї величини за проміжок часу t = t₂  t₁ визначають як середнє інтегральне і розраховують за формулою:

.

З цього рівняння випливає, що середнє значення синусоїдної величини за період буде дорівнювати нулю. Тому в електротехніці під середнім значенням синусоїдної величини, наприклад струму, розуміють середнє інтегральне значення його величини, але за половину періоду –

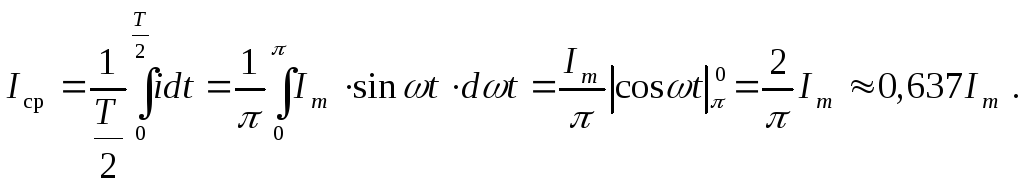
Між максимальним миттєвим (амплітудним) значеннями синусоїдних напруги й ЕРС та їх середніми значеннями є така залежність, відповідно:

,

.

Відношення амплітудного значення змінної електричної величини до середнього значення цієї величини називають коефіцієнтом форми кривої. При синусоїдному законі зміни величини (струму, ЕРС, напруги) коефіцієнт форми кривої, наприклад струму, буде: k_ф = I_m/I_ср = 1,11.

На практиці діючі і середні значення струму та напруги у колах змінного струму вимірюють електричними вимірювальними приладами – амперметром і вольтметром, відповідно. Ці прилади значно простіші за конструкцією і зручніші в експлуатації, ніж осцилографи. Амперметри та вольтметри, що призначені для вимірювання діючих значень, градуюють фактично за допомогою теплових приладів постійного струму, тому їх можна використовувати для вимірювань як в колах постійного, так і змінного струмів. Прилади, що призначені для вимірювання середніх значень електричних величин, використовують тільки в колах синусоїдного струму.

Застосування понять діюче і середнє значення електричної величини дало також можливість значно спростити розрахунки кіл змінного струму. Так, оскільки діюче і середнє значення електричної величини зв’язані з амплітудним (максимальним миттєвим) значенням цієї величини лінійними залежностями, то векторні діаграми зручніше будувати у діючих або середніх значеннях. Адже такі діаграми відрізняються від побудованих у амплітудних значеннях тільки лінійним масштабом.