8.3. Розгалужені електричні кола

Розрахунок сталих режимів в електричних колах синусоїдного струму істотно спрощується завдяки зображенню синусоїдних функцій часу (ЕРС, напруги, струму) комплексними числами, оскільки комплексне число складається з двох величин – модуля і аргумента, якщо це число за-писане в показниковій, або тригонометричній, формі, або дійсної та уяв-ної частин, якщо воно записане в алгебраїчній формі.

З математики відомо, що комплексними називають числа вигляду – це алгебраїчна форма запису комплексного числа:

, (8.36)

де – тригонометрична форма запису комплексного чис-ла; – модуль комплексного числа; – аргумент комплексного числа;

– показникова форма запису комплексного числа (рис.8.20);

; (у теоретичній електротехніці не користуються позначенням , оскільки літерою позначають миттєве значення струму) ; – основа натуральних логарифмів.

Згідно з рис. 8.20

; ; ; . (8.37)

У теорії електричних і магнітних кіл комплексне число позначають великою літерою з точкою зверху і визначають так:

, (8.38)

де – дійсна частина комплексного числа (Re від Real – дійсний ); – уявна частина комплексного числа (Im від Imagine – уявний).

Полярна форма запису комплексного числа така:

, (8.39)

де – модуль; – аргумент комплексного числа.

Кожний вектор, проведений з початку координат, можна зобразити символічно комплексним числом (див. рис. 8.20). Оскільки вектори зображають комплексними числами, дії на ними відповідають алгебраїчним діям над комплексними числами.

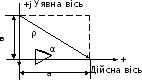
Рис.8.20

Наприклад треба додати два комплексних числа ; .

, (8.40)

де ; .

Отже, сума двох комплексних чисел є також комплексним числом, тобто це також вектор, який є геометричною сумою векторів, що відповідають комплексним числам додаваних векторів (рис. 8.21). Як бачимо, геометричному додаванню векторів відповідає алгебраїчне додавання комплексних чисел.

У результаті віднімання комплексних чисел ; дістаємо

, (8.41)

де ; .

Рис.8.21

Перемножувати комплексні числа , найзручніше в показниковій формі запису

, (8.42)

де – ; ,

або

, (8.43)

де – ; .

У результаті ділення комплексних чисел , дістаємо

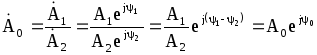, (8.44)

де ; ,

або

=

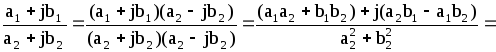
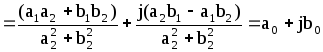, (8.45)

де ; .

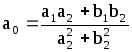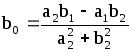Примітка. Множення комплексного числа на комплексний множник відповідає повороту вектора на кут у додатному напрямі ( тоб-то проти напряму руху годинникової стрілки). Потрібно запам’ятати спів-відношення, які часто використовуватимемо далі:

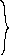
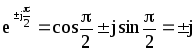, тобто ; ;

, тобто ; ; (8.46)

, тобто ; ;

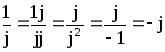, тобто ;

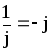; ; ; (8.47)

і т.д.

Дві комплексні величини, які мають рівні модулі і рівні, але протилежні за знаком аргумента, називають спряженими.

Якщо комплексне число

,

то спряжене йому комплексне число

.

Зазначимо властивості комплексних чисел і спряжених їм комплексних чисел:

; (8.48)

; (8.49)