
- •Часть I
- •§ 1. Тригонометрия.
- •Радианная мера угла.
- •Тригонометрические величины некоторых углов.
- •Выражение одних тригонометрических функций через другие.
- •Формулы приведения.
- •Значения обратных тригонометрических функций некоторых углов.
- •Формулы решения простейших тригонометрических уравнений.
- •Частные случаи простейших тригонометрических уравнений.
- •§ 2. Таблица квадратов натуральных чисел от 10 до 99.
- •§ 3. Формулы преобразования многочленов.
- •Формулы сокращённого умножения.
- •Следствия из формул сокращённого умножения.
- •§ 4. Средние величины.
- •Неравенства между средними величинами:
- •§ 5. Модуль и его свойства.
- •§ 6. Степени и корни.
- •§ 7. Арифметическая прогрессия.
- •§ 8. Геометрическая прогрессия.
- •§ 9. Область определения функции.
- •§ 10. Множество значений функции.
- •§ 11. Чётность, нечётность, периодичность функции.
- •§ 12. Производная функции.
- •§ 13. Первообразная функции.
- •§ 14. Показательная функция.
- •§ 15. Логарифмы и логарифмическая функция.
- •§ 17. Графики элементарных функций.
- •§ 16. Факториал и его свойства.
- •§ 17. Основные математические постоянные.
- •§ 18. Конечные числовые суммы.
- •§ 19. Часто используемые неравенства.
- •400002, Волгоград, Университетский пр-т, 26
§ 12. Производная функции.
Для функции
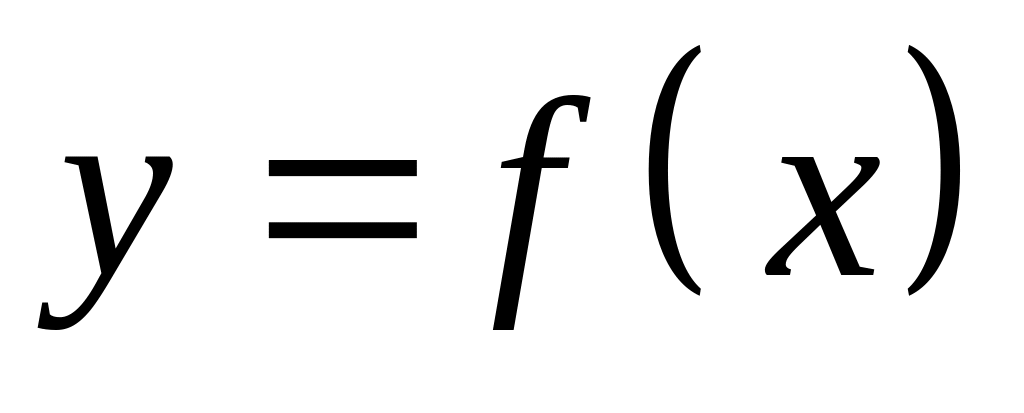 по определению
по определению
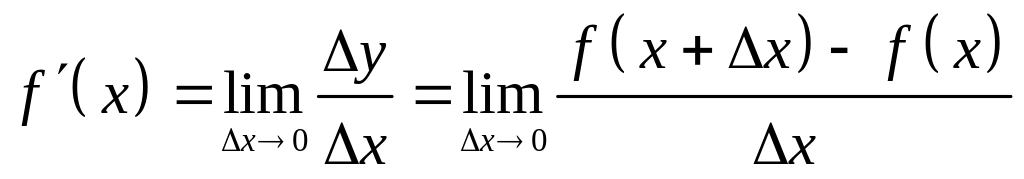 .
.Правила нахождения производных.
![]() ,
,
![]() ,
,
![]() ,
,
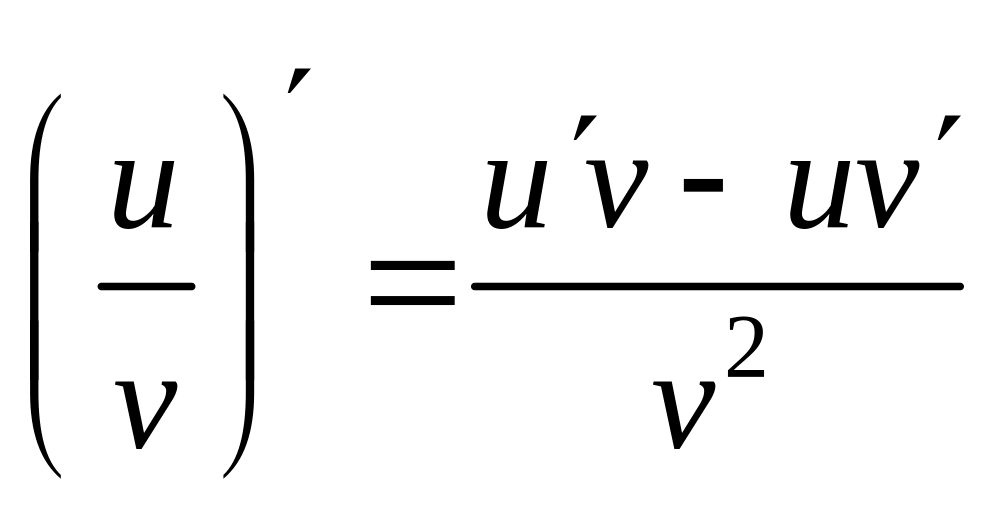 ,
где
,
где
![]() ,
,
![]() ,
.
,
.
Таблица производных элементарных функций.
|
|
|
|
|
|
|
|
С |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение касательной к графику функции в точке
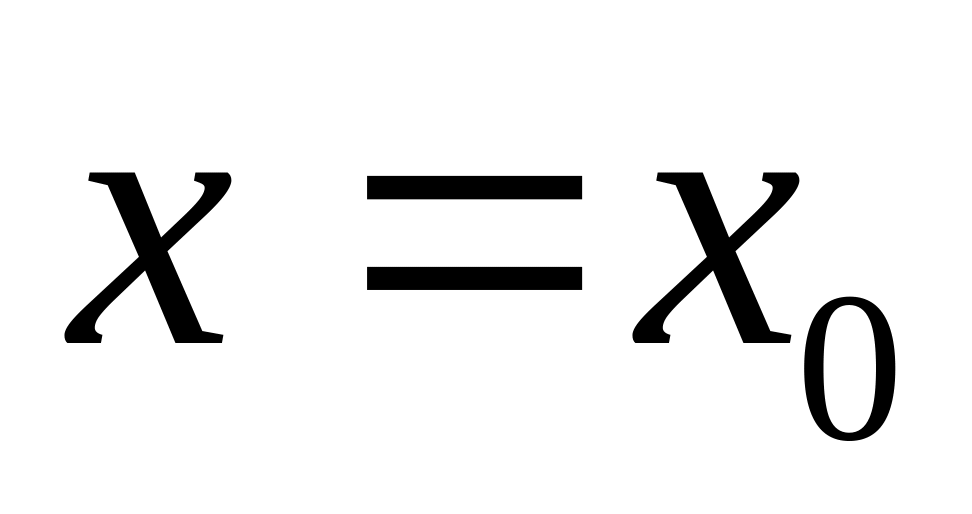 :
:
![]() .
.
Геометрический смысл производной:
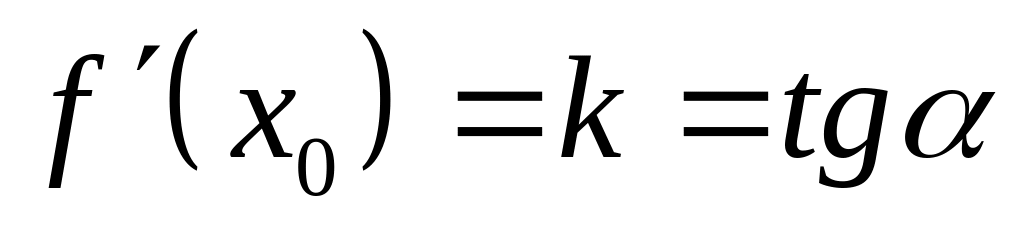 ,
где
,
где
![]() - угловой коэффициент касательной
- угловой коэффициент касательной
![]() к графику функции
в точке
,
- угол, образованный касательной с
положительным направлением оси
.
к графику функции
в точке
,
- угол, образованный касательной с
положительным направлением оси
.
Физический (механический) смысл производной.
Если
![]() - зависимость пути от времени движения
тела, то его скорость и ускорение
вычисляются по формулам:
- зависимость пути от времени движения
тела, то его скорость и ускорение
вычисляются по формулам:
![]() и
и
![]() .
.
Производная сложной функции: если
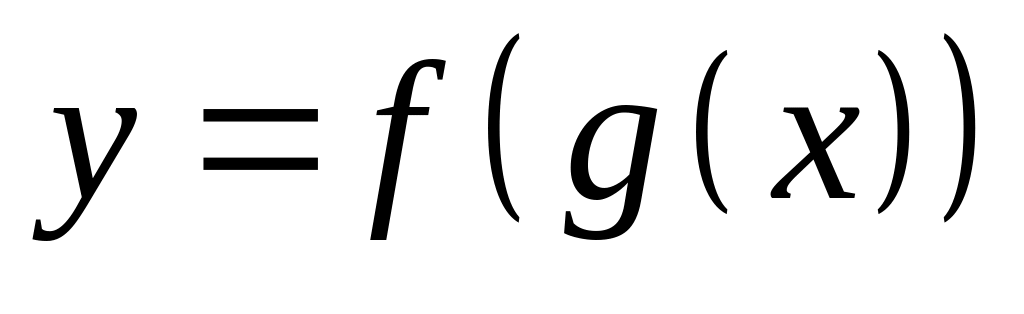 ,
то
,
то
 .
.Производная обратной функции: если
 и
и
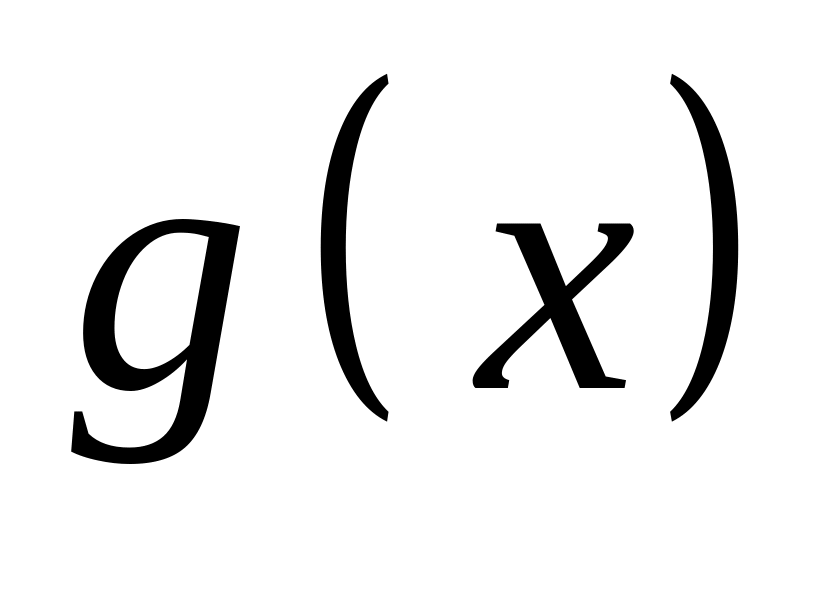 - взаимообратные функции и существуют
- взаимообратные функции и существуют
 ,
,
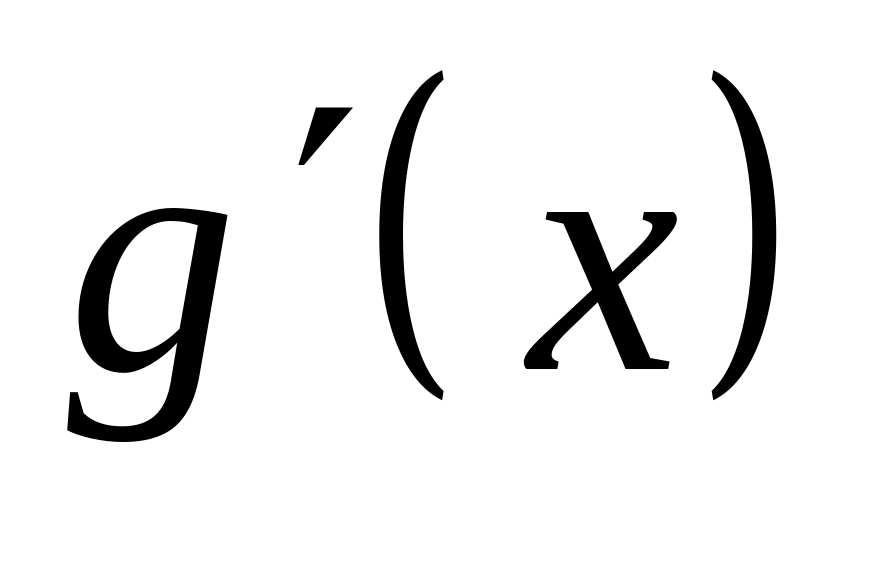 ,
причём
,
причём
 ,
то
,
то
 .
.
§ 13. Первообразная функции.
Определение. Функция
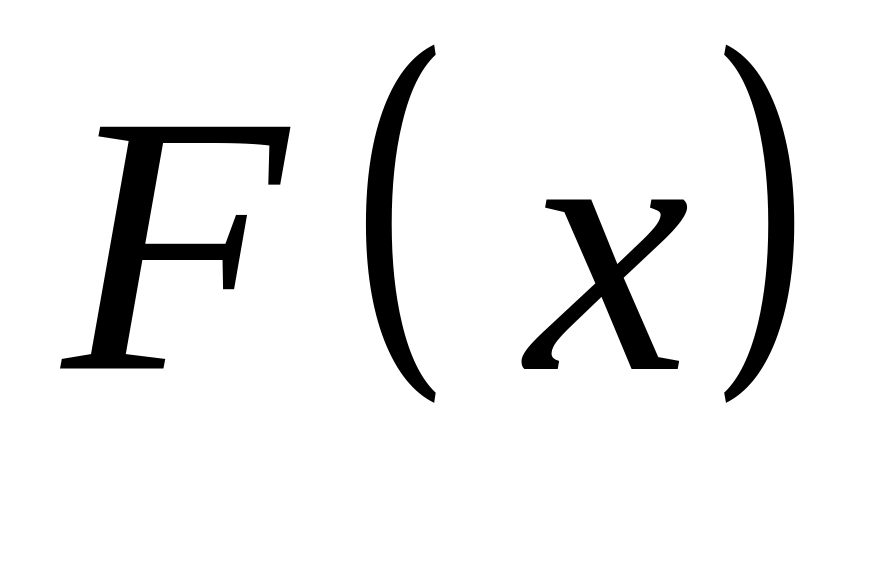 называется первообразной для функции
называется первообразной для функции
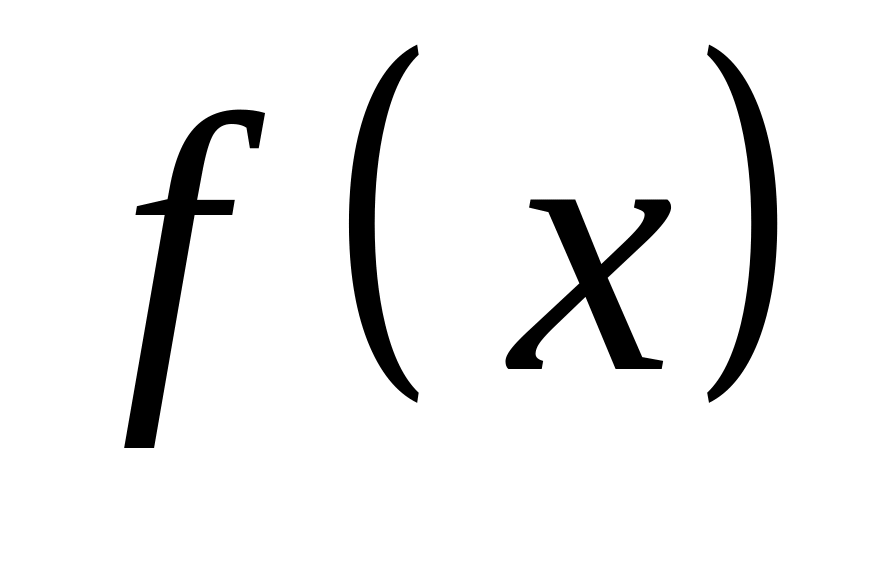 на множестве
на множестве
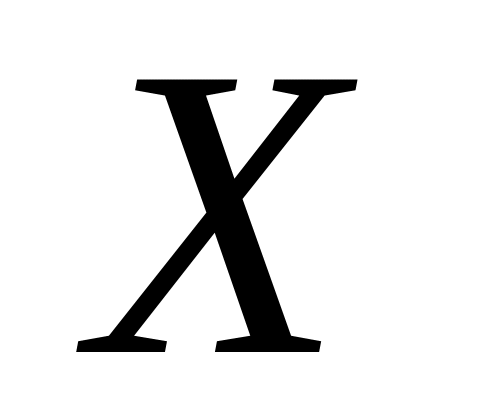 ,
если для любого
,
если для любого
 верно равенство
верно равенство
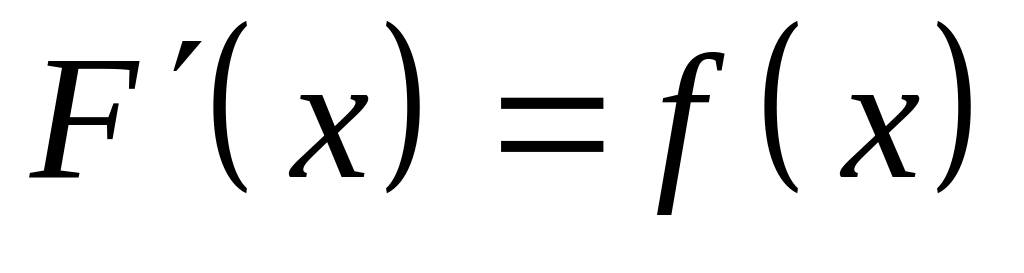 .
.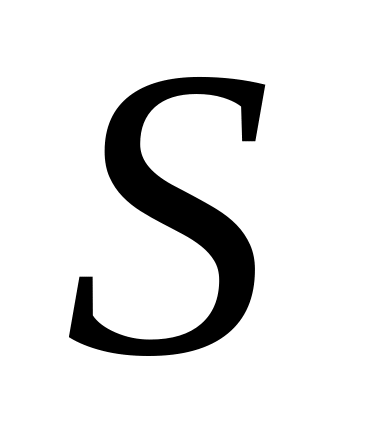 - площадь фигуры, ограниченная графиком
функции
- площадь фигуры, ограниченная графиком
функции
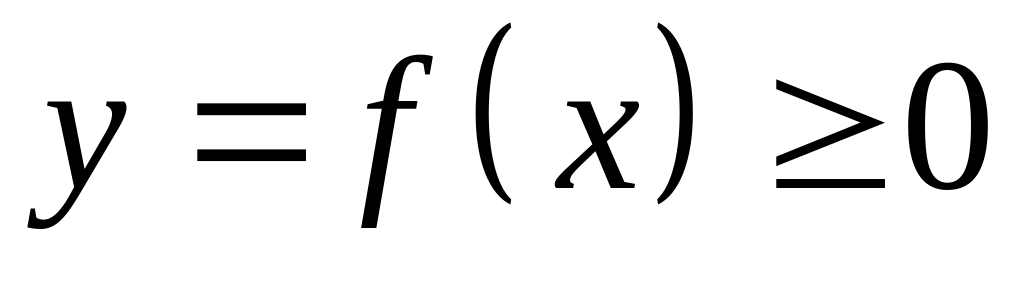 ,
осью
и прямыми
,
осью
и прямыми
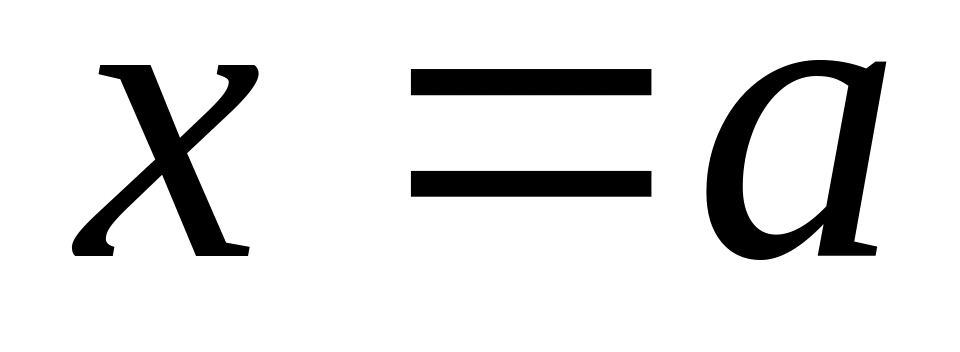 ,
,
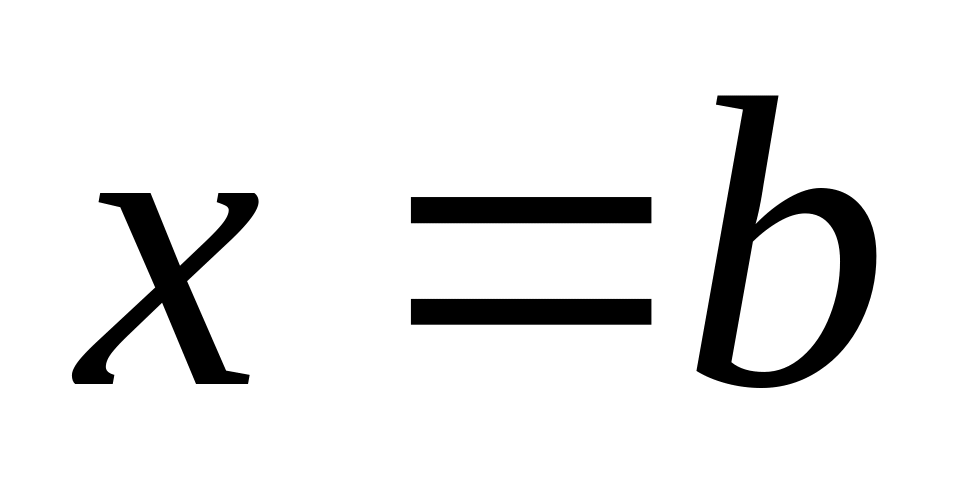 ,
,
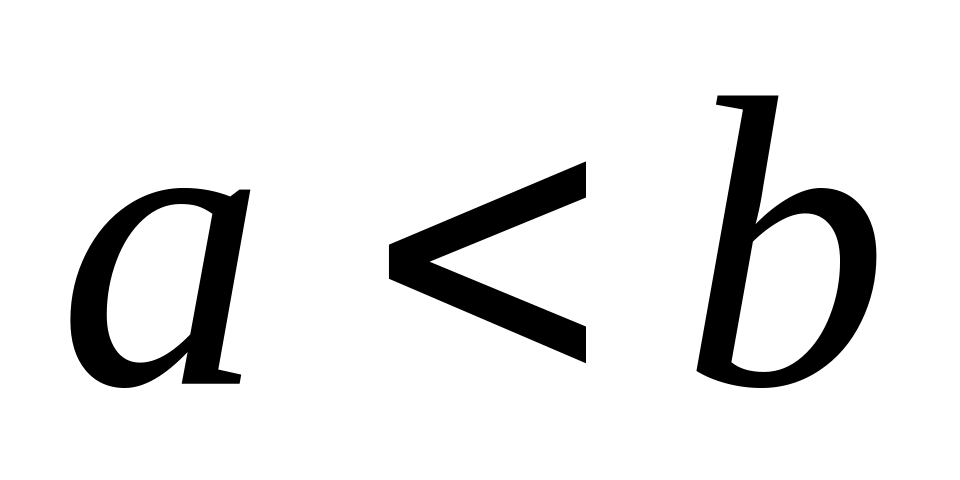 вычисляется по формуле Ньютона-Лейбница:
вычисляется по формуле Ньютона-Лейбница:
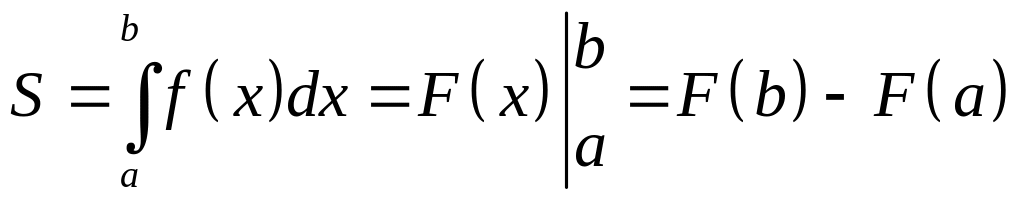 .
.
Таблица первообразных элементарных функций.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 14. Показательная функция.
Определение. Функция вида , где ,
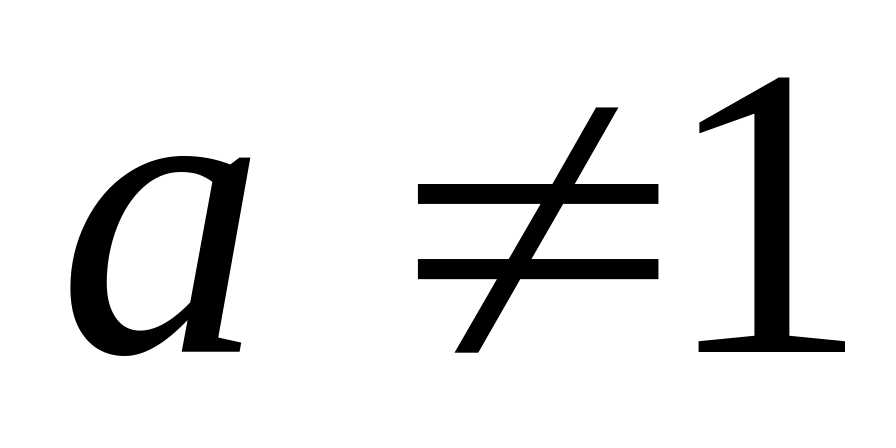 ,
называется показательной с основанием
.
,
называется показательной с основанием
.Область определения или - любое число.
Множество значений
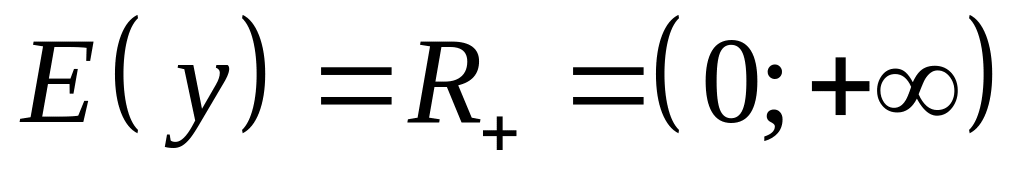 или
.
или
.Функция непрерывна на всей области определения.
График функции проходит через точку
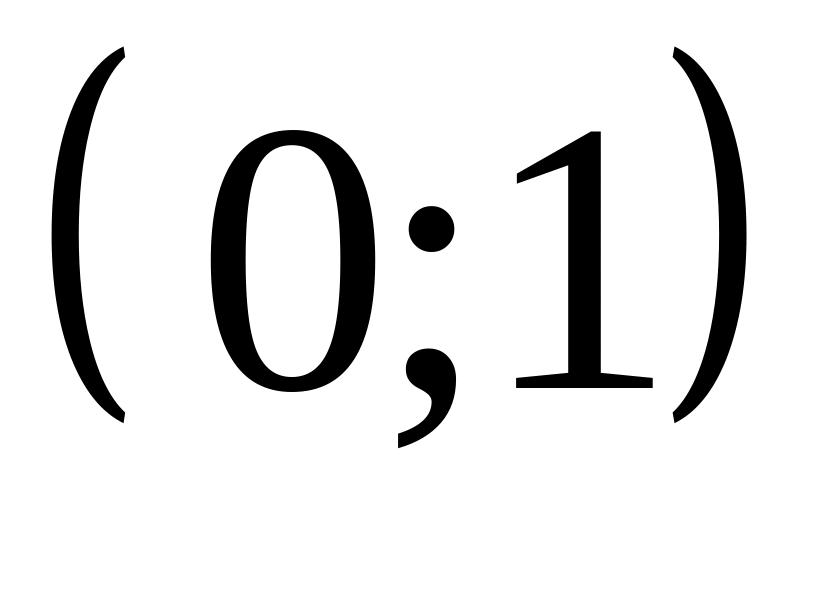 и расположен выше оси
.
и расположен выше оси
.Функция
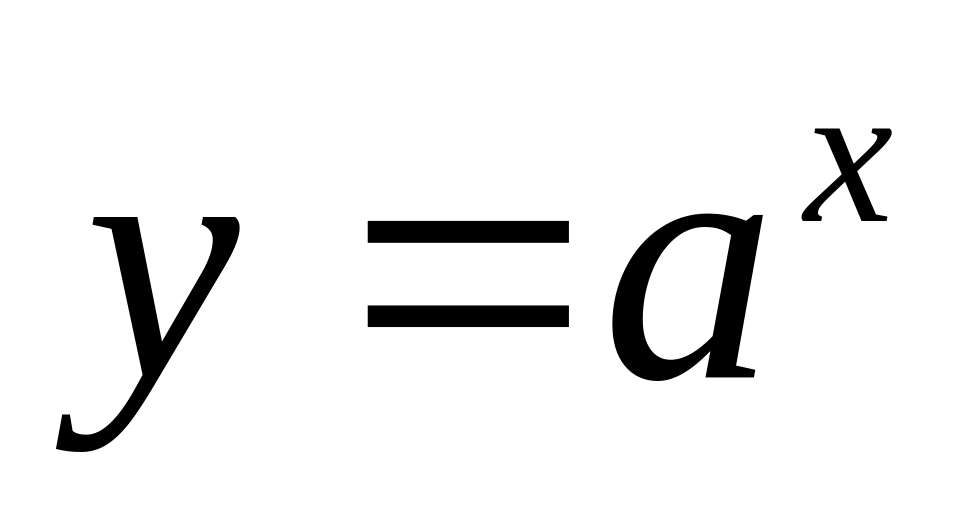 убывает при
убывает при
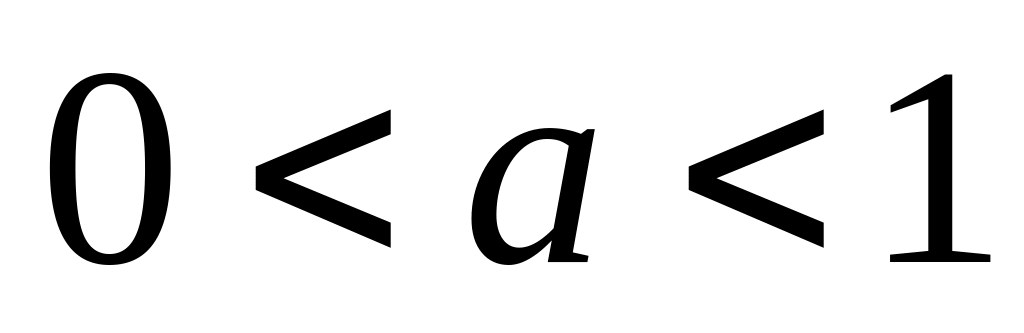 ,
возрастает при
,
возрастает при
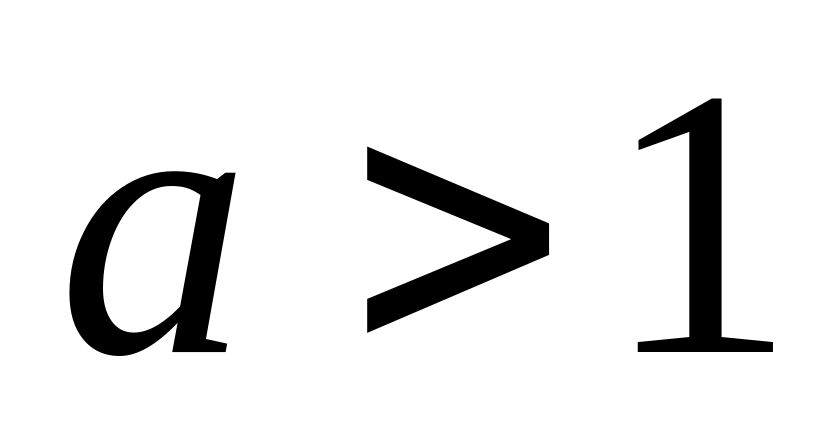 .
.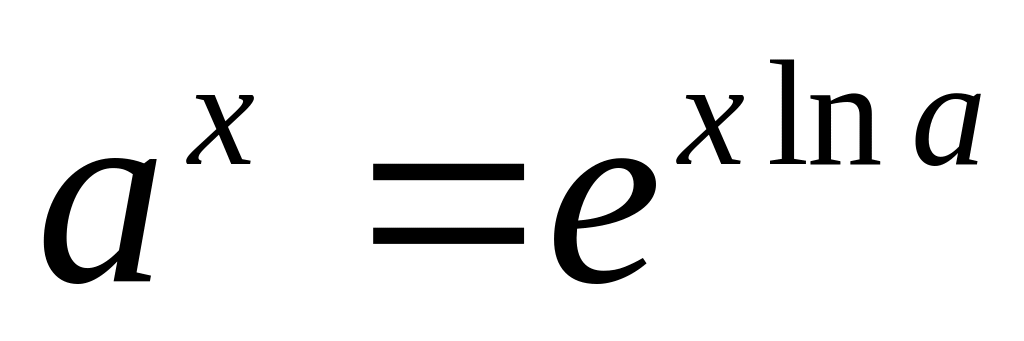 ,
где
,
.
,
где
,
.Решение простейших показательных уравнений:
![]() ,
,
,
,
![]() .
В уравнениях, приводимых к квадратным,
делают замену переменной
.
В уравнениях, приводимых к квадратным,
делают замену переменной
![]() ,
,
![]() .
.
Решение показательных неравенств:
 ;
;
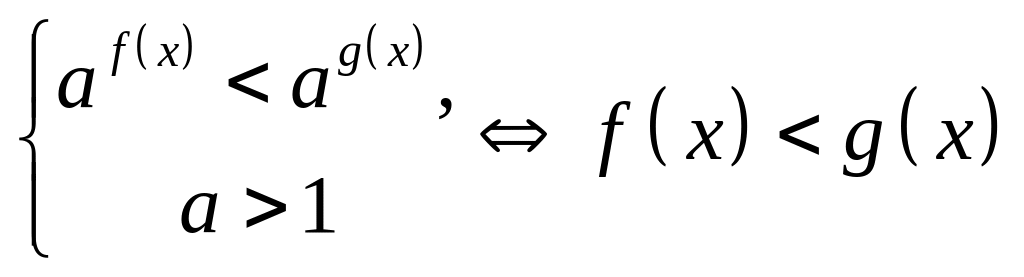 .
.
Аналогично расписываются неравенства
с другим знаком
![]() ,
,
![]() ,
,
![]() в первой строке.
в первой строке.
§ 15. Логарифмы и логарифмическая функция.
Определение. Логарифмом положительного числа
 по основанию
по основанию
 ,
(
,
(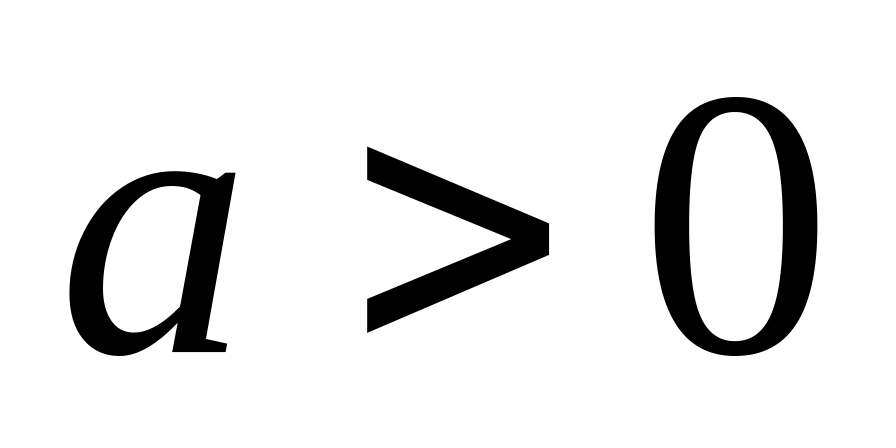 ,
,
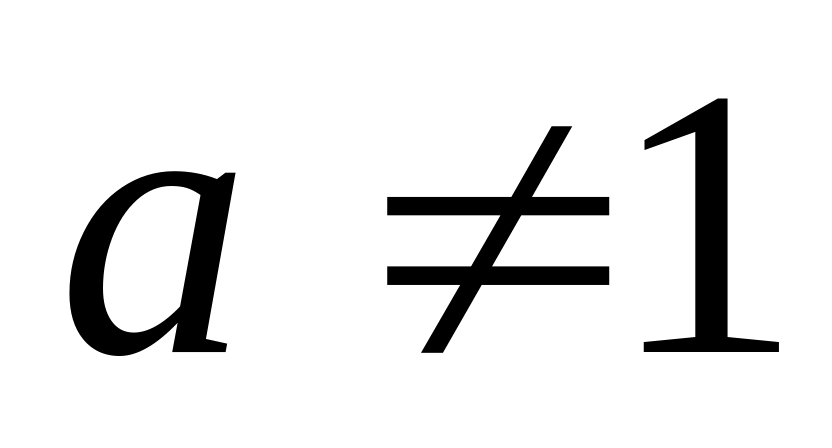 )
называется показатель степени
)
называется показатель степени
 ,
в которую нужно возвести основание
,
чтобы получить
:
,
в которую нужно возвести основание
,
чтобы получить
:
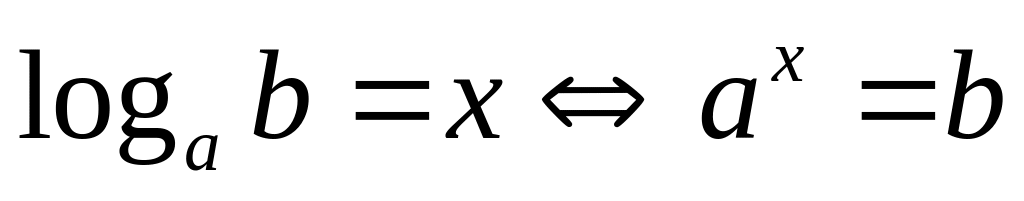 .
.Свойства логарифма:
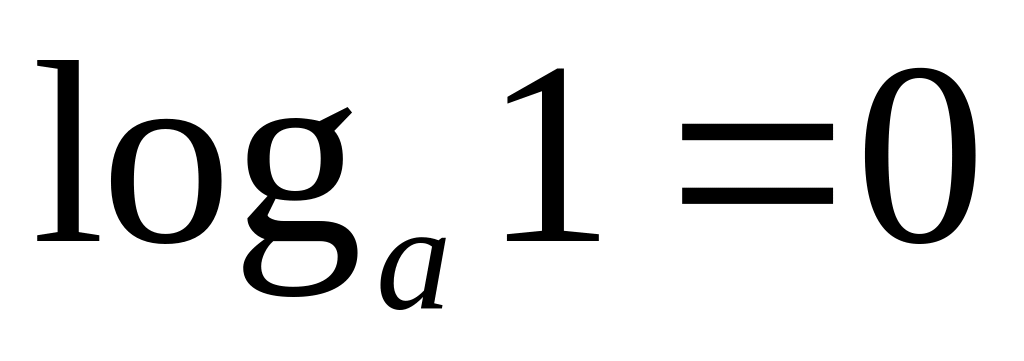 ,
,
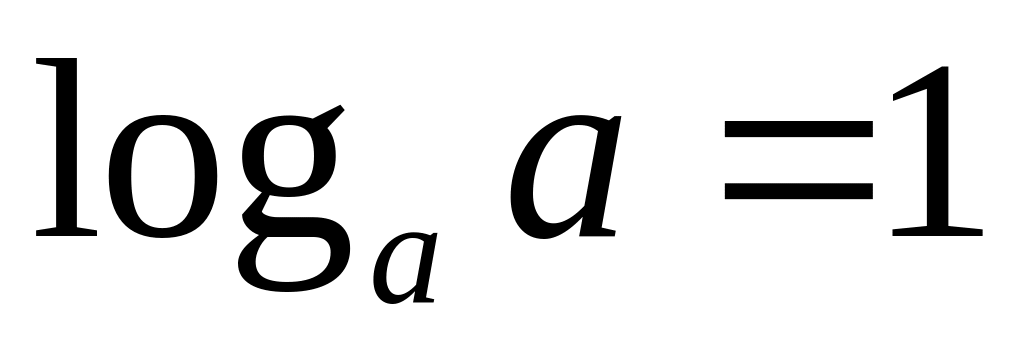 ,
,
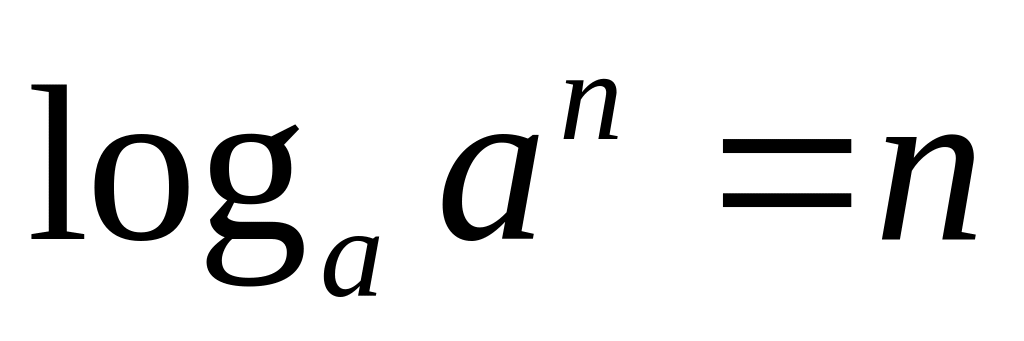 ,
,
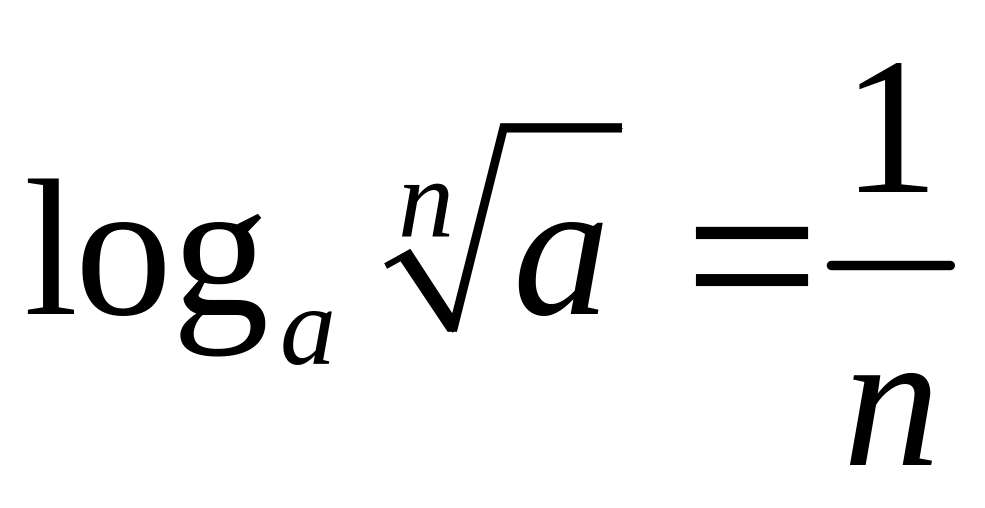 .
.Десятичные логарифмы:
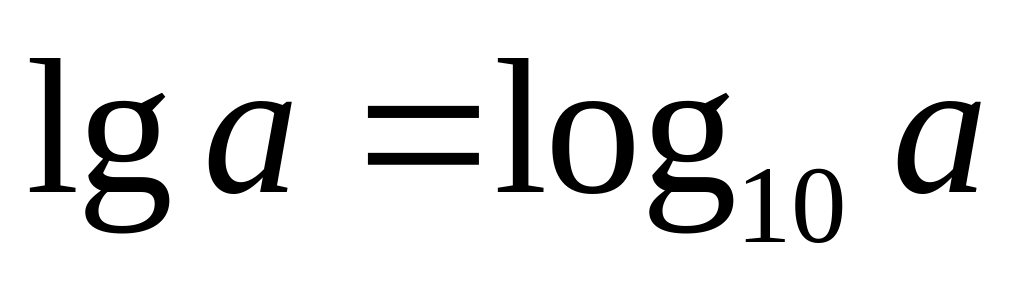 ,
натуральные:
,
натуральные:
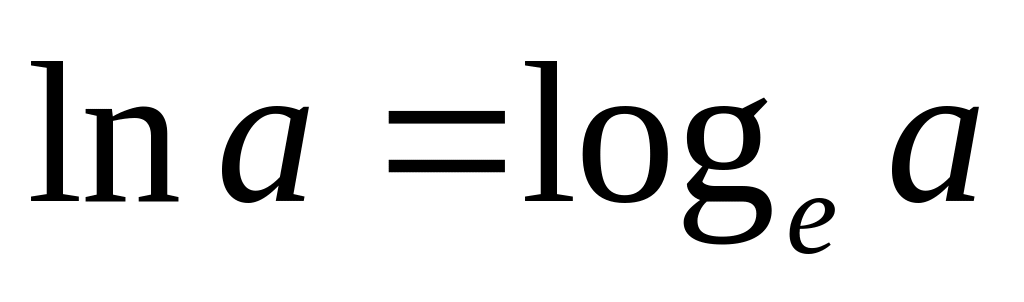 ,
,
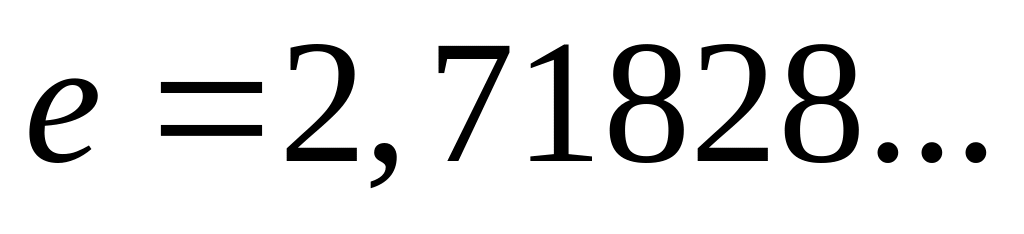
Основное логарифмическое тождество:
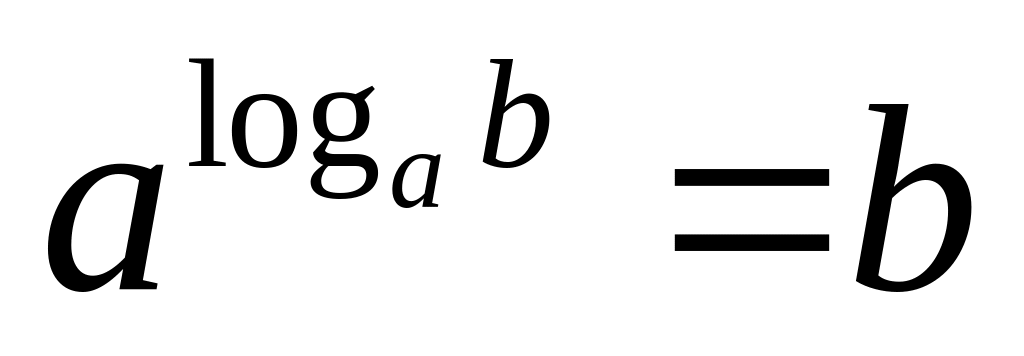 ,
,
,
,
,
,
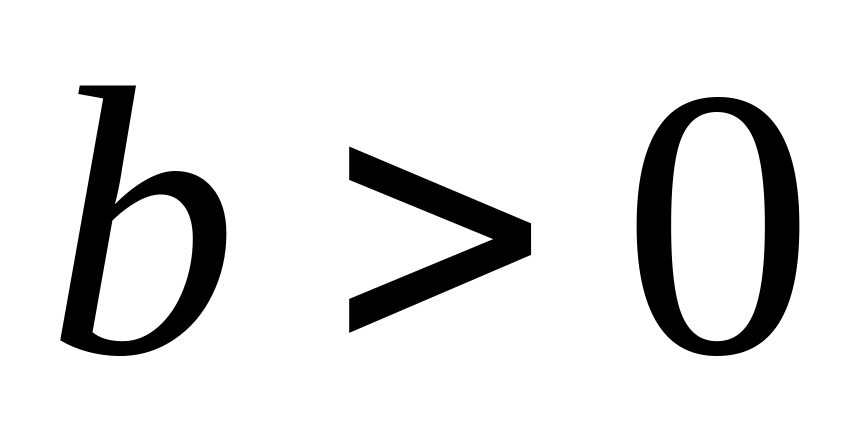 .
.Сумма логарифмов:
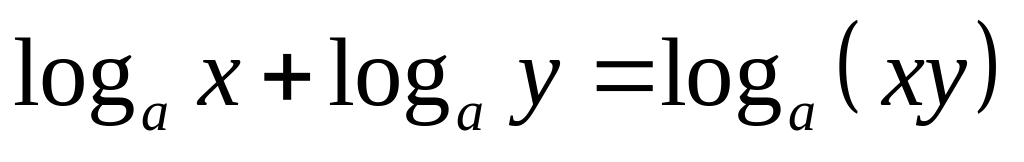 ,
,
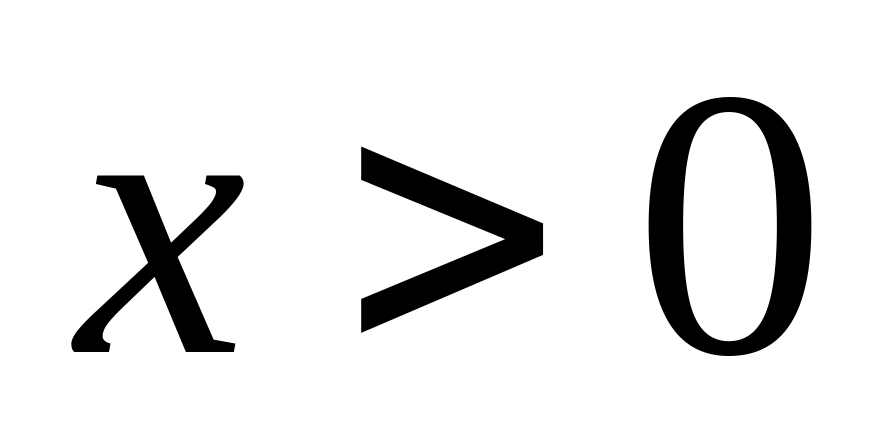 ,
,
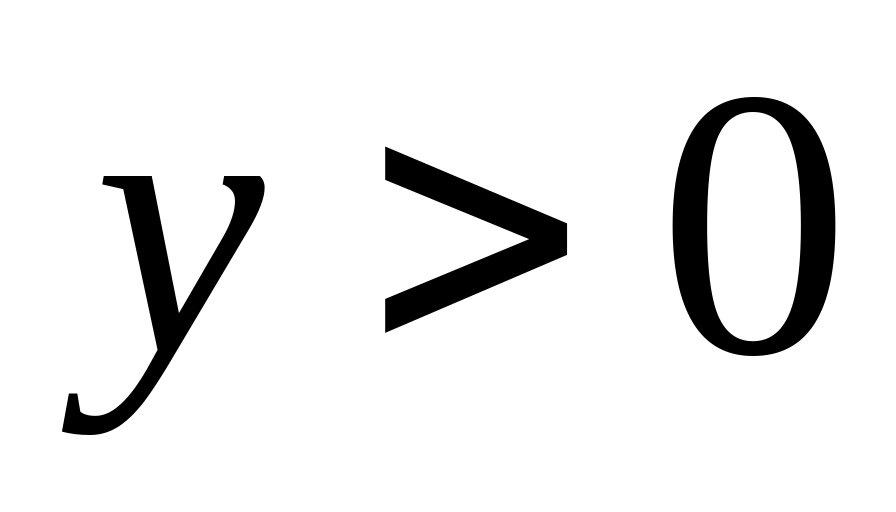 .
.Разность логарифмов:
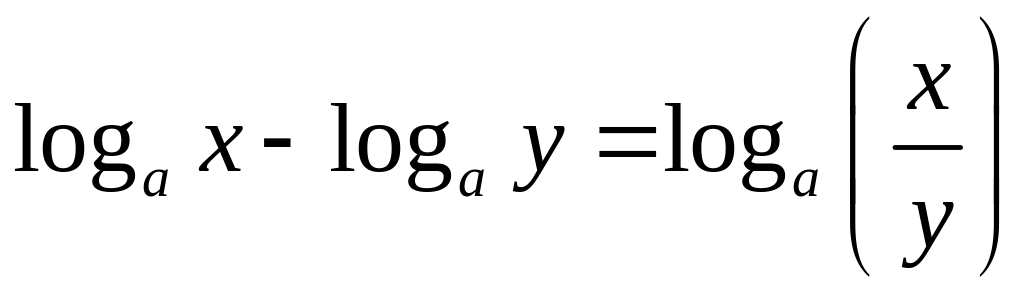 ,
,
.
,
,
.Логарифм степени:
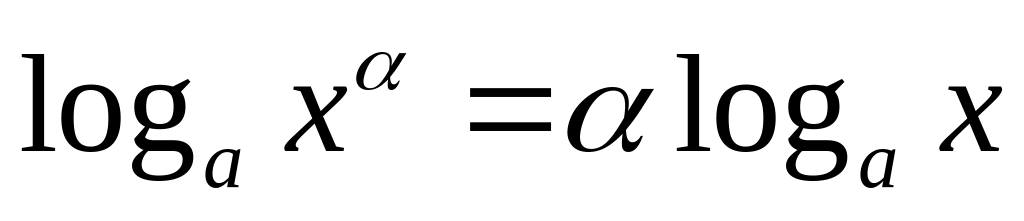 ,
;
,
;
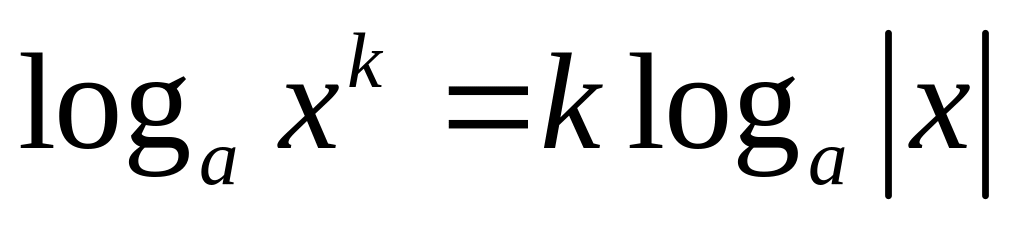 ,
,
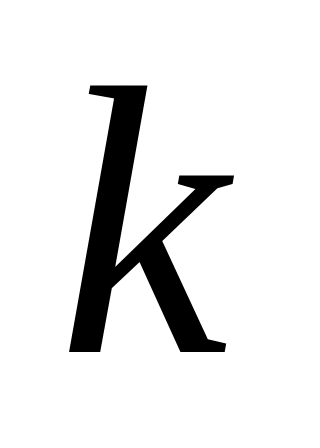 - чётное целое;
- чётное целое;
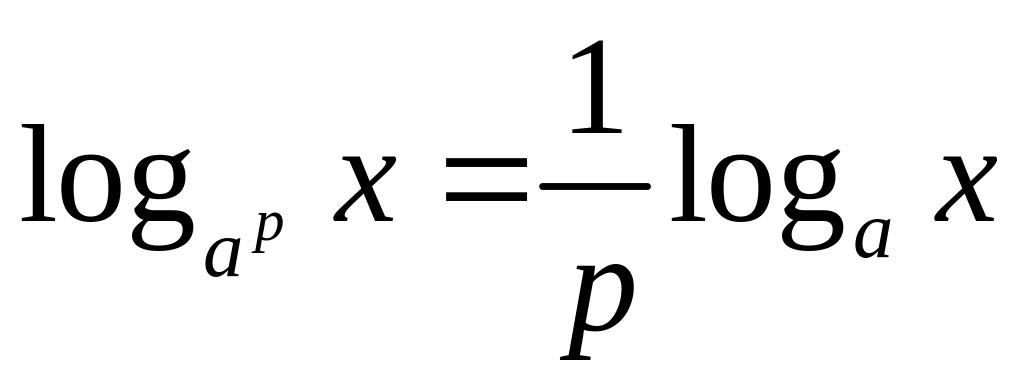 ,
,
 ,
,
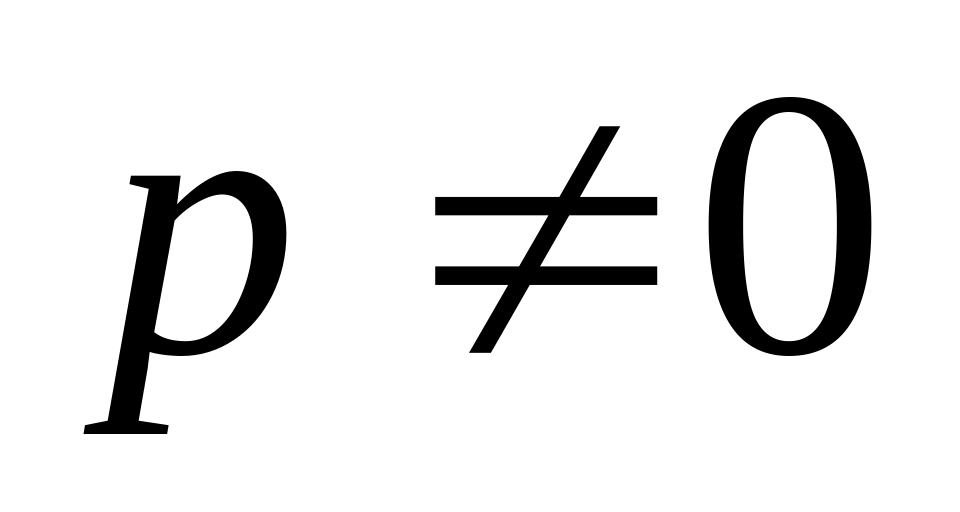 ;
;
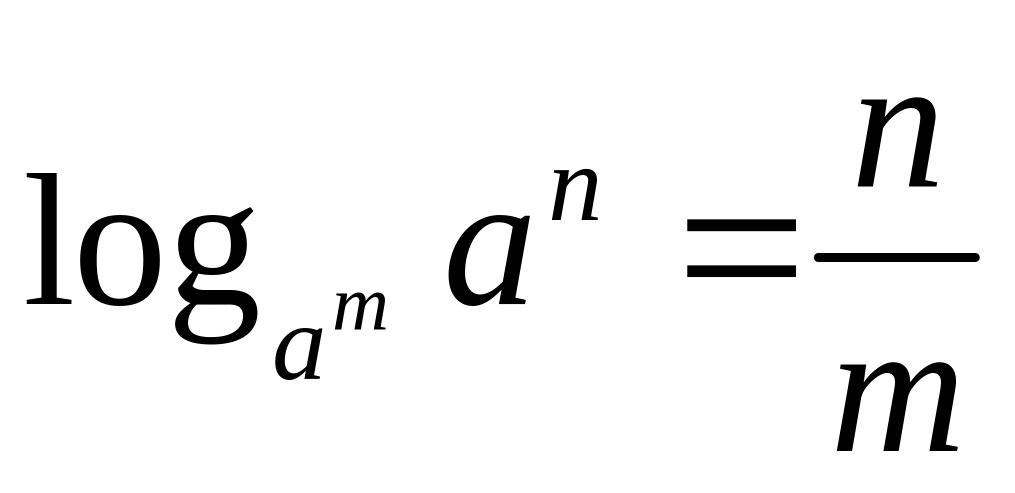 ,
,
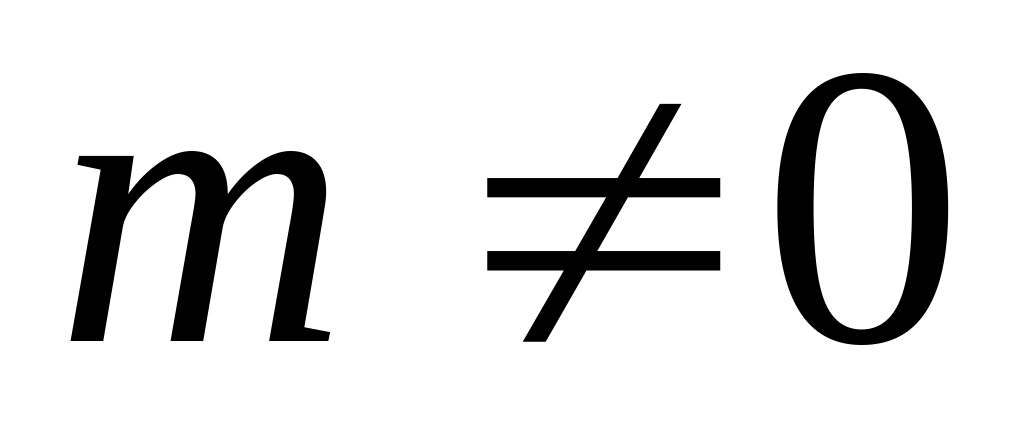 .
.Переход к новому основанию:
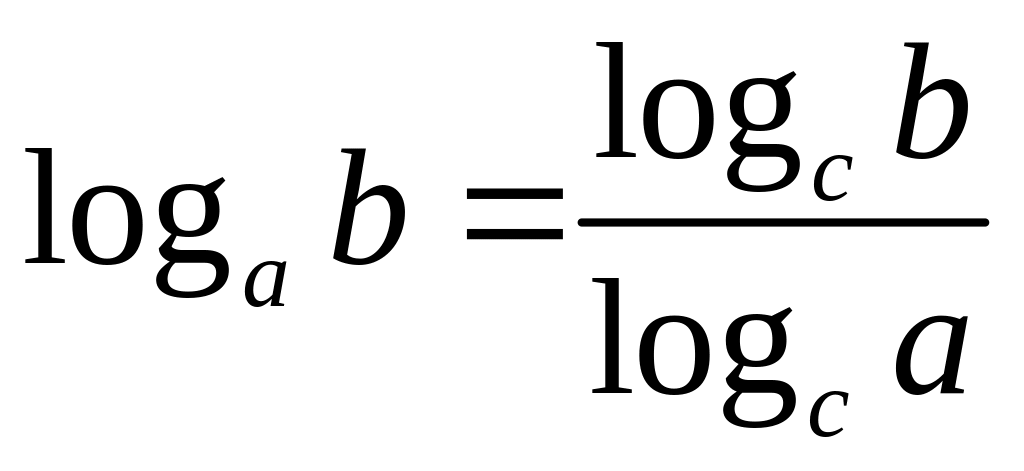 ,
,
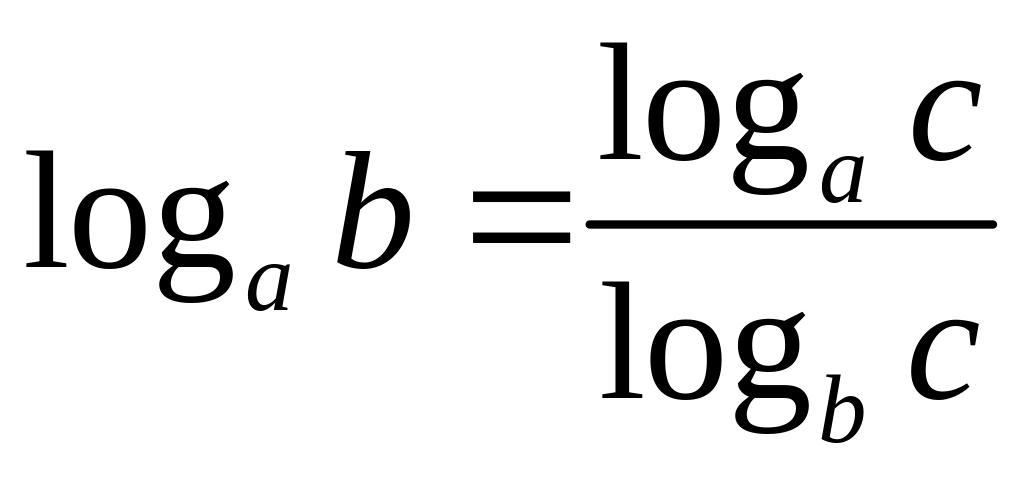 ,
,
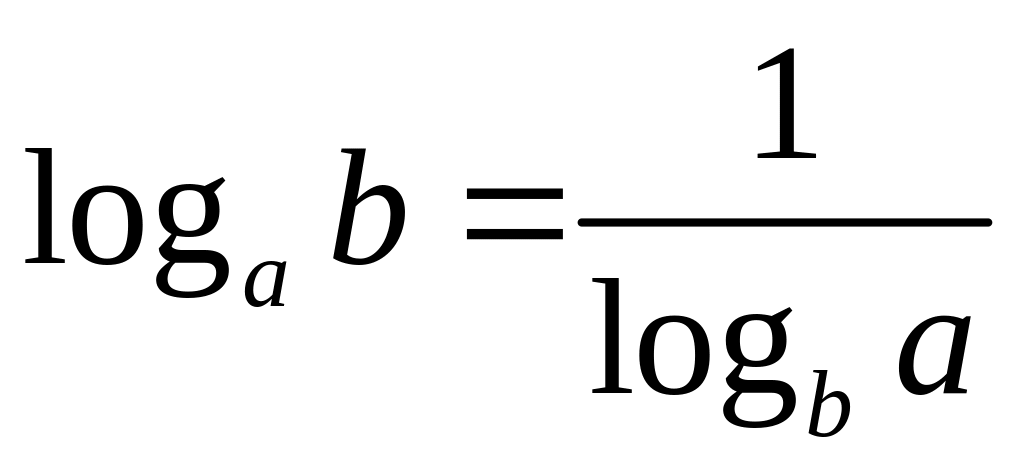 .
.Переход к новому основанию:
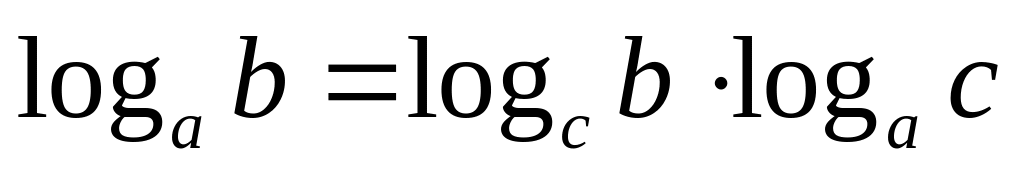 .
.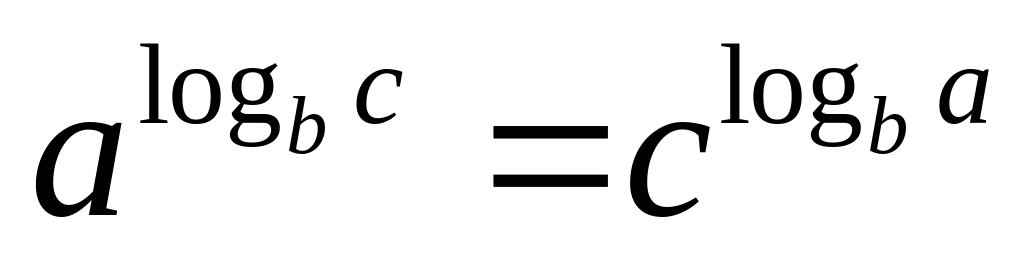 ;
;
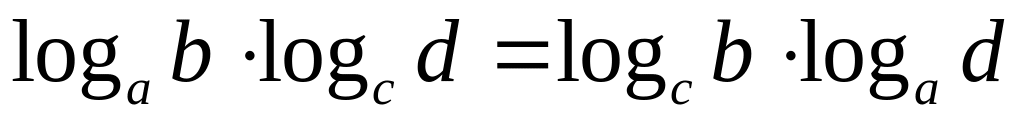 .
.Функция вида , где , , называется логарифмической.
Область определения и множество значений логарифмической функции
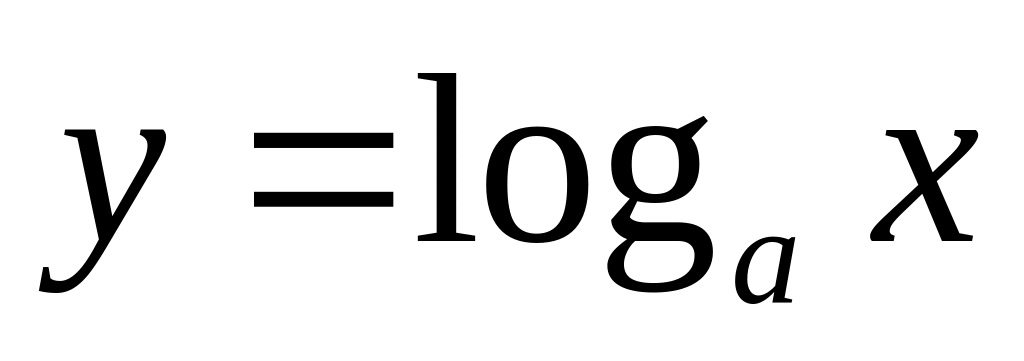 :
:
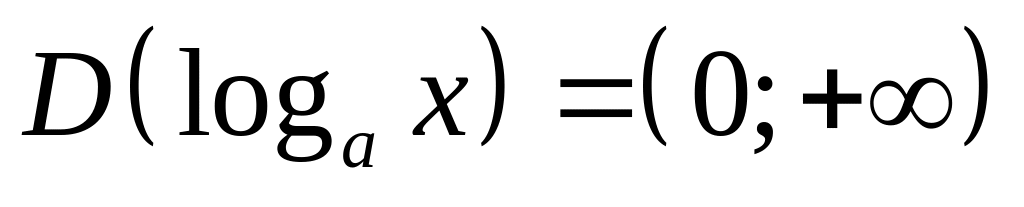 или
;
или
;
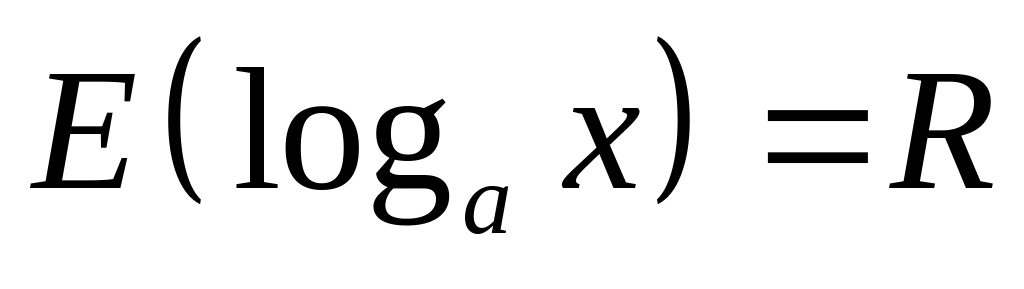 .
.
Для сложной логарифмической функции
![]() область определения задаётся системой
условий:
область определения задаётся системой
условий:
![]() ,
,
![]() ,
,
![]() .
.
Функция непрерывна на всей области определения.
График функции проходит через точку
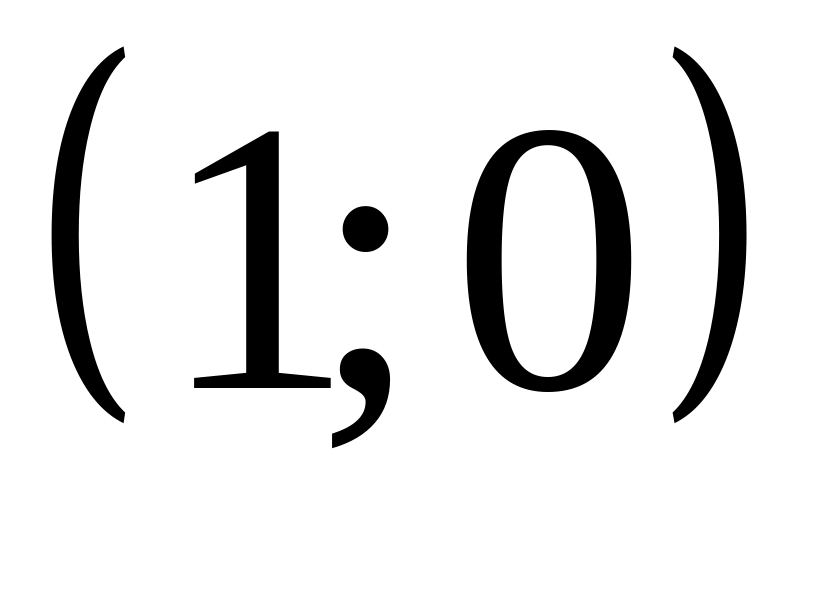 и расположен справа от оси
.
и расположен справа от оси
.Функция убывает при , возрастает при .
Решение простейших логарифмических уравнений:
![]() ;
;
 При этом учитывается то неравенство,
которое проще.
При этом учитывается то неравенство,
которое проще.
В уравнениях, приводимых к квадратным,
делают замену переменной
![]() .
.
Решение логарифмических неравенств:
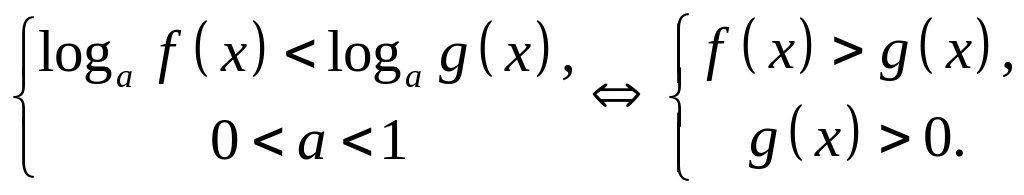
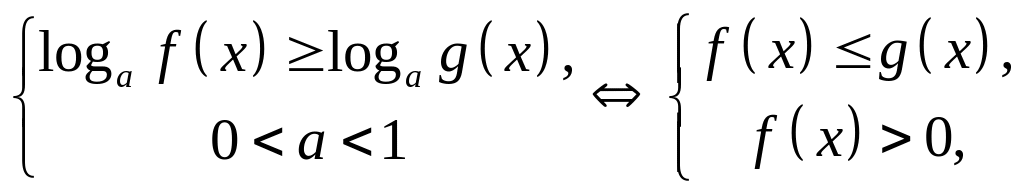
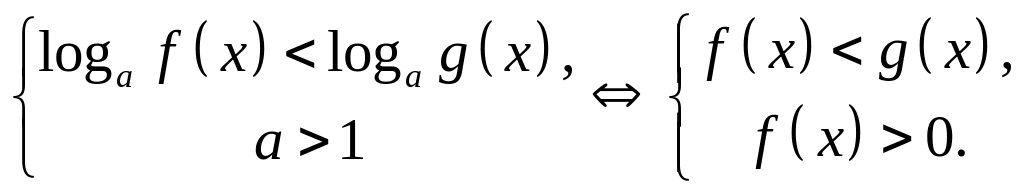

Аналогично расписываются неравенства с другими знаками , в первой строке.
Знак
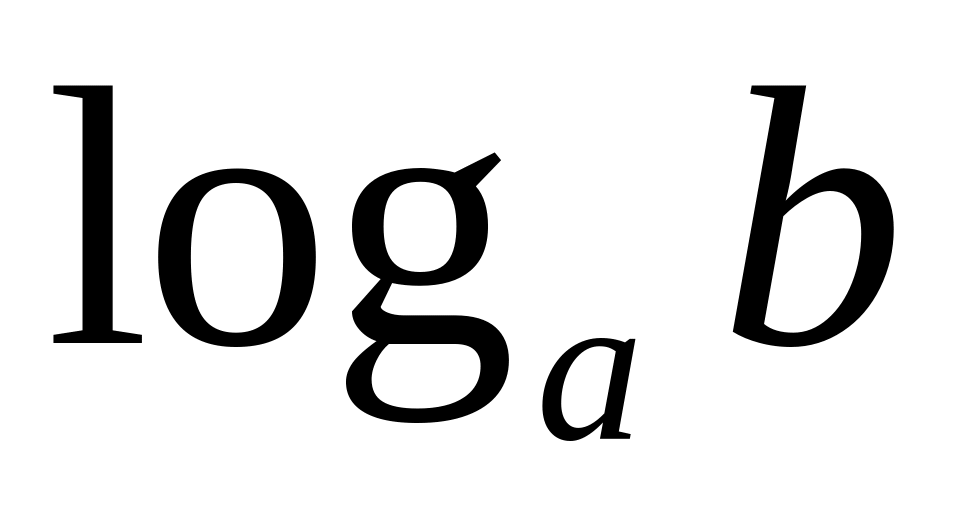 совпадает со знаком произведения
совпадает со знаком произведения
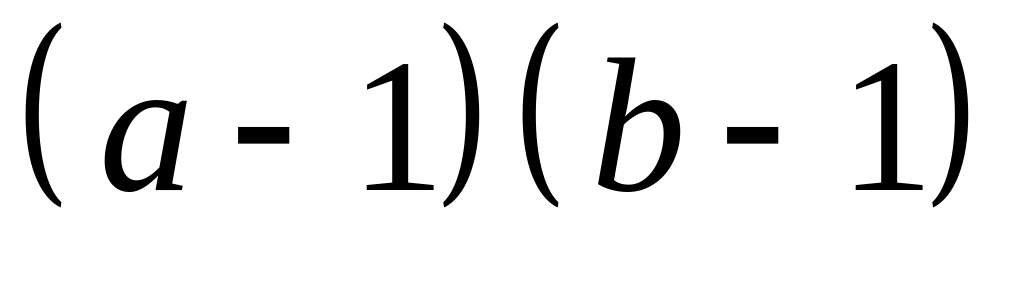 :
:
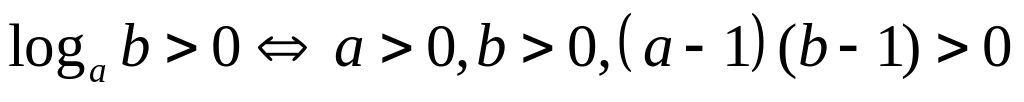 ,
,
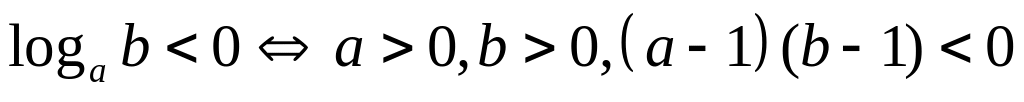 .
.
