Энтропия системы, совершающей необратимый процесс, возрастает

. (4)

Выражения (3) и (4) относятся только к замкнутым системам.

Таким образом, энтропия замкнутой системы может либо возрас­тать, либо оставаться постоянной. Это можно представить неравенством Клаузиуса

(5)

Этот принцип лежит в основе еще одной формулировки второго начала термодинамики: все реальные процессы изменения состояния в изоли­рованной системе протекают с увеличением энтропии.

Состоянию равновесия системы соответствует максимально возмож­ное значение энтропии

(6)

К. Больцман дал энтропии молекулярно-кинетическое толкование как меры перехода упорядоченных форм движения частиц вещества в беспорядочное (тепловое) движение. При этом он установил связь между энтропией и термодинамической вероятностью системы; энтропия S изменяется пропорционально логарифму термодинамической вероятности W

S=klnW, (7)

где k -постоянная Больцмана.

Термодинамическая вероятность - это число комбинаций из элементов, составляющих систему, при которых может осуществляться данное состояние системы.

Для идеального газа, например, макросостояние (давление, объ­ем и температура газа) обусловлено совокупностью микросостояний составляющих газ молекул (их скоростями, массами, распределением в объеме газа). Термодинамическая вероятность макросостояния газа- это число микросостояний, при которых возможно данное макросостояние. Нетрудно заключить, что наибольшая вероятность соответствует равномерному распределению молекул по всему объему газа с установившимся значением средней кинетической энергии, т.е. состоя­нию, при котором все молекулы газа находятся в равновесном теп­ловом движении. Этому состоянию соответствует и максимальная энтро­пия. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности сис­темы. Процессы в замкнутой системе идут в направлении увеличения числа микросостояний, т.е. от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет макси­мальной.

ПРАКТИЧЕСКАЯ ЧАСТЬ.

В данной работе определяют изменение энтропии при нагревании припоя от комнатной температуры до температуры плавления и при его плавлении. Полное изменение энтропии при нагревании и плавлении припоя

, (8),

где и - изменение энтропии соответственно при нагревании припоя от комнатной температуры до температуры плавление и при полном плавлении.

Вычислим изменение энтропии

(9)

При нагревании (участок 1 - 2 на рис.1)

(10),

с - удельная теплоемкость твердого припоя, m- масса припоя.

При плавлении (участок 2 - 3 на рис.1)

(11),

где - удельная теплота плавления.

t,мин

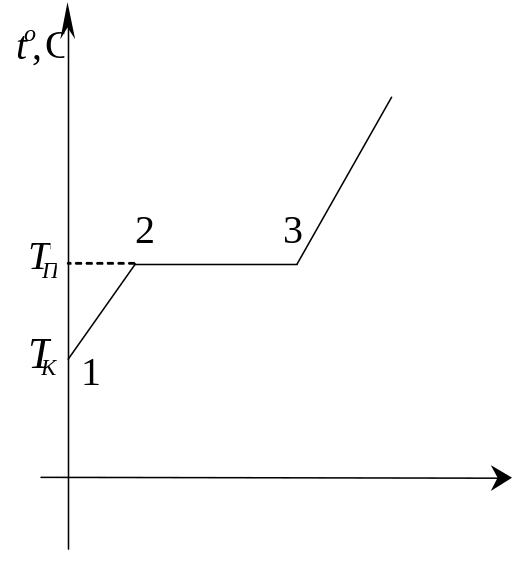
Рис. 1.

Тогда 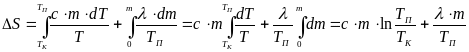, или

. (12)

Р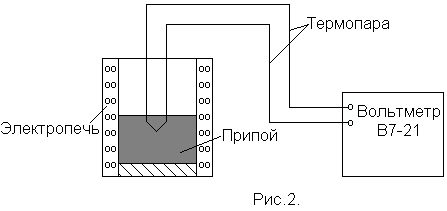 абочая схема установки приведена на рис.2. В данной работе температура припоя измеряется термопарой хромель-алюмель (см. Примечание).

Один контакт термопары погружен в припой, помещенный в электро­печь, другой - находится при комнатной температуре. При включении электропечи происходит нагревание и плавление припоя. Его темпера­туру определяют из градуировочного графика (приведен на панели ус­тановки) по значениям термоЭДС , которые измеряются электронным вольтметром В7 - 21.