ВСТУП

Зі створенням та впровадженням комп’ютерної техніки в наукові розрахунки, управління, проектування та інші сфери діяльності людини з’явилася потреба в математичних моделях опису структури та функціонування нових класів об’єктів та виникло прагнення максимально використовувати розумові здібності людини шляхом впровадження комп’ютерів в сам процес пізнання.

З’явилися нові розділи математики, що були призначені підтримувати процеси проектування та використання комп’ютерів.

Дисципліна “ Алгоритми та методи обчислень” забезпечує теоретичну та практичну підготовку по розробці програм для розв’язання математичних завдань, які виникають при розробці систем із складною структурою, алгоритмів керування апаратурою ЕОМ.

Основною метою лабораторних робіт з дисципліни є отримання практичних навичок з комп’ютерної математики.

Результатом виконання лабораторних робіт має стати створення студентом програм на алгоритмічній мові з використанням комп'ютерної техніки для розв’язання інженерних та економічних задач.

Методичні вказівки містять 7 лабораторні робот.

Лабораторна робота №1 Розв’язання нелінійних та трансцендентних рівнянь.

Мета роботи – оволодіти здібностями обчислення приблизних значень дійсних коренів алгебраїчних та трансцендентних рівнянь числовими методами: половинного ділення, пропорційних частин, Рибакова та методом простих ітерацій на ЕОМ.

1.1 Теоретичні положення.

Необхідно знайти розв’язки рівняння:

f(x) = 0 /1/

де f(x) визначена та неперервна на деякому скінченому або нескінченому інтервалі a < x >b. Якщо функція є поліномом, тоді рівняння /1/ називається алгебраїчним, якщо ж у функцію f(x) входять елементарні (тригонометричні, логарифмічні, показникові і т.д.) функції, то таке рівняння називається трансцендентним.

Будь-яке значення x, що обертає функцію в нуль, тобто таке, при якому f(x)= 0, називається коренем рівняння /1/, а спосіб знаходження цього значення і є розв’язанням рівняння /1/.

Знайти корені рівняння вигляду /1/ точно вдається лише в деяких випадках. Крім того, часто рівняння містять коефіцієнти, що відомі лише приблизно і точне визначення коренів неможливе. Для цього і були розроблені методи числового розв’язання рівнянь виду /1/, які дозволяють знаходити приблизні значення коренів цього рівняння.

При цьому доводиться вирішувати дві задачі:

• відділення коренів, встановлення достатньо малих інтервалів , в яких міститься ізольований корінь рівняння /1/

• уточнення коренів до заданої точності.

Для приблизного знаходження дійсних коренів або відділення коренів використовують різні методи. В деяких випадках межі коренів можна визначати з фізичних явищ, що описуються рівнянням /1/.

Іноді для приблизного визначення коренів знаходять простіше рівняння, яке має корені, що приблизно дорівнюють кореням даного рівняння.

Одним з найпростіших методів знаходження приблизного значення коренів є побудова графіку функції y = f(x) та приблизне визначення точок, в яких крива перетинає вісь X. У цих точках y = 0 і відповідне значення x є дійсним коренем рівняння /1/. В деяких випадках рівняння /1/ ліпше записати у вигляді , а потім побудувати графік двох функцій і . Абсциси точок перетину задовольняють рівнянню , а отже, і рівнянню /1/.

Для уточнення дійсних коренів до заданої точності використовуються ітераційні методи. Використання того чи іншого методу залежить і від початкового наближення до кореня, існування та гладкість похідних функцій необхідної кількості коренів, їх кратності і т.д.

В ітераційних методах можна вибирати критерій закінчення процедури пошуку. Якщо функція f(x) в заданій області змінюється повільно, тобто f(x)<1, то ітераційний процес слід припинити при виконанні умови x_k+1-x_k< , де x_k, x_k+1 - наближення до кореня. Якщо ж функція змінюється швидко, тобто f^(x)1, то ітераційний процес буде закінчуватися з виконанням умови: f(x)< .

1.2 Числові методи розв’язання нелінійних рівнянь.

Існує багато методів числового розв’язання нелінійних рівнянь. Розглянемо чотири з них: метод половинного ділення, метод пропорційних частин (хорд), метод Рибакова і метод простих ітерацій.

1.2.1 Метод половинного ділення

Цей метод використовується, коли відомо, що f(x) неперервна на відрізку [A,B] і f(A) f(B)<0.

Суть методу полягає в наступному. Ділимо відрізок [A,B], на якому шукаємо корінь рівняння, навпіл і, якщо f((A+B)/2)  0, обираємо ту з половин A, (A+B)/2 чи (A+B)/2, B, на кінцях якої f(x) має протилежні знаки. Новий відрізок знову ділимо навпіл і повторюємо доки не отримаємо корінь рівняння з заданою точністю.

Метод половинного ділення зручно застосовувати для грубого знаходження кореня даного рівняння, тому що із збільшенням точності зростає об’єм роботи, що буде виконуватися, через повільну збіжність ітераційного процесу.

Опишемо схему методу. До початку обчислення задаємо число  точність, з якою треба отримати корінь рівняння.

Потім:

1). надамо значення x₀ = A; x₁ = B;

2). для кожного шагу процесу :

обчислюємо x = (x₀ + x₁ )/2, , y = f(x); та перевіряємо нерівність y і, якщо нерівність виконується, тоді вважаємо коренем рівняння;

якщо нерівність не виконується, тоді, якщо y f(x)>0 надамо x₀ значення x; а інакше надамо x₁ значення x та повторюємо обчислення з пункту 2).

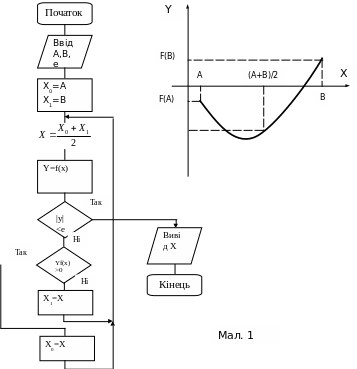
Дамо геометричну інтерпретацію методу половинного ділення.

Нехай функція f(x) має графік зображений на мал. 1. При обчисленні значення (A+B)/2 знаходимо середину відрізку [A,B]. Обчислення величини f((A+B)/2) означає опускання перпендикуляра з точки (A+B)/2 до перетину з графіком функції f(x). Якщо f(x) > , тоді для подальшого розгляду обираємо той відрізок, на кінцях якого f(x) приймає значення різних знаків. У даному випадку це відрізок(A+B)/2, B. На цьому шаг ітераційного процесу закінчується. Повторюємо доки не буде виконана умова закінчення ітераційного процесу.