Часть 2. История развития вычислительной техники
2.1. Первые счетные машины
2.1.1. Абак и счеты
Древнейшим счетным инструментом человека была его собственная рука. Имена числительные указывают, что у первобытного человека орудием счета были пальцы. Например, в древнерусской нумерации единицы называются «перстами», десятки – «составами». От пальцевого счета берет начало пятеричная (одна рука), десятеричная (две руки) и двадцатеричная (пальцы рук и ног) системы счисления.
Издревле употреблялся инструментальный счет с помощью деревянных палочек с зарубками (бирок). Бирка разрезалась на две продольных части, одна оставалась у крестьянина, другая – у сборщика налогов. Другие народы использовали для представления чисел и счета ремни или веревки с узелками.
Бирки и веревки с узелками не могли удовлетворить потребности в средствах вычисления. Развитию же письменного счета препятствовали два обстоятельства. Во-первых, пергамент был слишком дорог, а бумага появилась значительно позже (в Европе – около XI столетия). Во-вторых, в тогдашних системах счисления письменно выполнить все необходимые операции было сложно. Попробуйте, например, перемножить два числа в римской системе счисления. Этим можно объяснить появление специального счетного прибора, известного под названием абака.
Абак – это греческое слово, которое переводится как «счетная доска». Простейшая форма абака действительно представляла собой специальную доску. На ней острой палочкой проводились линии, и какие-нибудь предметы, например камешки и палочки, размещались в получившихся колонках по позиционному принципу. А чтобы они не скатывались, доска покрывалась слоем песка или пыли.
В России счеты появились на рубеже XVI-XVII в.в. Долгое время считалось, что они ведут свое происхождение от китайского суаньпаня, но в 60-х годах было доказано оригинальное, русское происхождение этого счетного прибора. У него, во-первых, горизонтальное расположение спиц, а, во-вторых, используется десятичная, а не пятеричная система.
Первоначально термина «счеты» не существовало и прибор именовался «дощаным счетом».В XVII-XVIII в.в. в России счеты уже широко использовались в торговле и различных учреждениях. Они применялись при начальном обучении арифметике в качестве учебного пособия. Хотя форма счетов неизменна уже свыше 250 лет, было предложено немало модификаций этого элементарного прибора. Следует обратить внимание на счетный прибор Ф.М.Свободского. В нем были специальные счетные поля для запоминания промежуточных результатов. Также им были разработаны правила сведения арифметических действий к последовательности сложений и вычитаний.
2.1.2. Палочки Непера и логарифмическая линейка
Начало XVII в. ознаменовалось новыми достижениями инструментального счета. Они связаны с именем шотландского математика Джона Непера, важным изобретением которого явились логарифмы. Это позволило заменить умножение и деление сложением и вычитанием. Появившиеся логарифмические таблицы упростили вычисления, но все же они оставались трудоемкими для тех, кому приходилось заниматься этим ежедневно. Поэтому вслед за изобретением логарифмов делаются попытки механизировать логарифмические вычисления.
Непер, возможно, знал о так называемом методе gelosia (жалюзи). От этого метода до палочек Непера – один шаг. В 1617 г. (Рис. 2.1). Непер описывает счет с помощью палочек. Этот прибор под названием «палочки Непера» быстро получил широкое распространение в Европе и был в одно время даже более популярен, чем логарифмы.
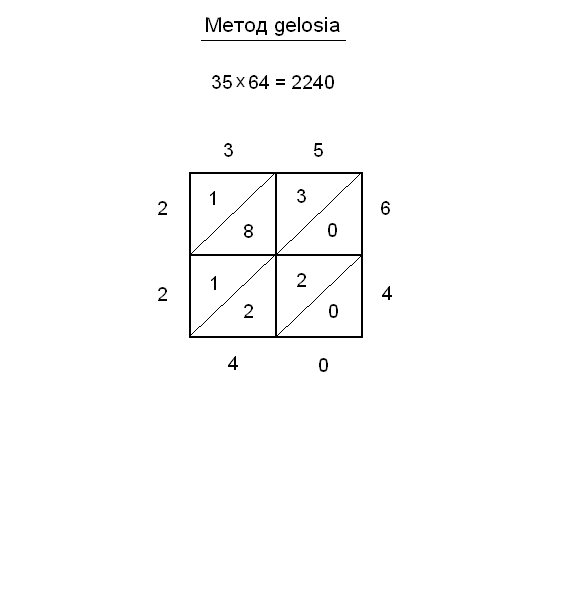
Изготовить его очень просто. Он состоит из 10 основных палочек, на которых помещена таблица умножения. Правая 11-я палочка неподвижна, а все остальные могут менять свои места. В каждом квадрате таблицы проведены диагонали, ниже которых записаны единицы получаемых произведений, а выше – десятки.
С помощью прибора Непера можно производить умножение и деление чисел, причем умножение заменяется сложением, а деление – вычитанием. Если, например, нужно умножить число 2085 на 4, то для этого ставят рядом палочки, имеющие сверху цифры 2,0,8,5, и обращают внимание на клетки этих палочек, стоящие в одной строке с цифрой 4 на крайней правой палочке.
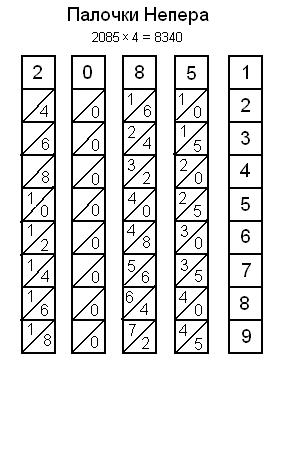
Числа складываются параллельно диагоналям квадратов: 8, 3+0=3, 2+2=4, 0. Искомое произведение равно 8340. Итак, палочки Непера давали значительное упрощение в счете.
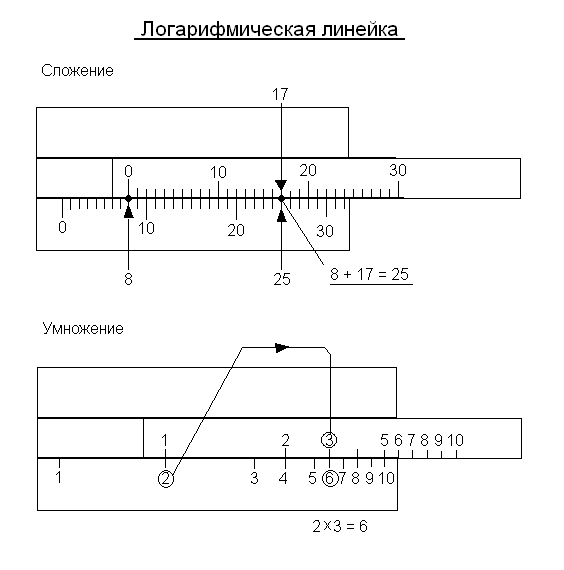
Изобретение логарифмов послужило основой для изобретения замечательного вычислительного инструмента – логарифмической линейки. Её прародительницей является логарифмическая шкала, известная под названием «шкала Гюнтера». Она представляет собой прямолинейный отрезок, на котором откладывались логарифмы чисел или тригонометрических величин. Несколько таких шкал наносилось на деревянную или металлическую пластинку параллельно. Циркули-измерители использовались для сложения и вычитания отрезков вдоль линий шкалы, что в соответствии со свойствами логарифмов позволяло находить произведение или частное.
Изобретателем первой логарифмической линейки стал английский математик Уильям Отред. . Независимо от Отреда похожую логарифмическую линейку изобрел Ричард Деламейн.Изобретателем же первой универсальной логарифмической линейки следует считать английского механика Джона Уатта. В 1779 г. он сконструировал линейку, пригодную для выполнения любых инженерных расчетов. В своей линейке Уатт расположил ряд шкал весьма разумным образом, их градуировка была выполнена с большой точностью, что позволило привлечь к ней внимание широких кругов.
Принципиально новую шкалу предложил П.-М. Роже. Он на движок линейки нанес обычную логарифмическую шкалу, а на неподвижную часть линейки – шкалу повторного логарифма, т.е. log(log(n)). В силу логарифмических соотношений линейка Роже позволяла при одном перемещении движка возводить одно число в степень другого. Идея важного элемента линейки – бегунка, была впервые высказана великим Ньютоном.
Позволяя производить расчеты с двумя-тремя точными цифрами, логарифмическая линейка долгое время оставалась одним из основных счетных приборов инженера.