1.3.8Перевод чисел из смещенной системы счисления с натуральным основанием в ссок и обратно

3.2.3.1. Как отмечалось в подразделе 3.1.1.5, ССОК имеет дело с целыми положительными числами. Поэтому будем полагать, что ,

т.е. 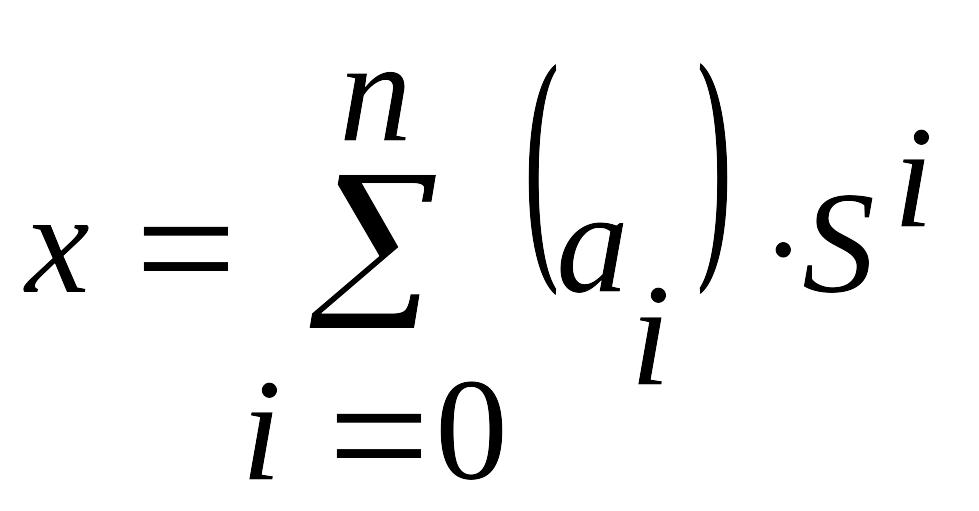. (3.15)

Предположим также, что заданы основания ССОК , являющиеся взаимно простыми числами, причем 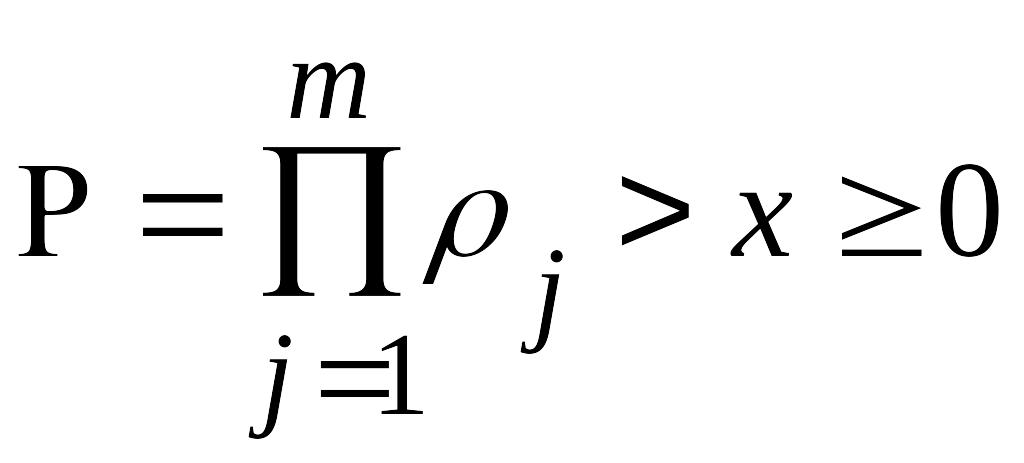. Последнему условию удовлетворяет, очевидно, и каждое из ( ) в соотношении (3.15). Тогда на основании выражений (3.4) и (3.5) можно написать, что , где

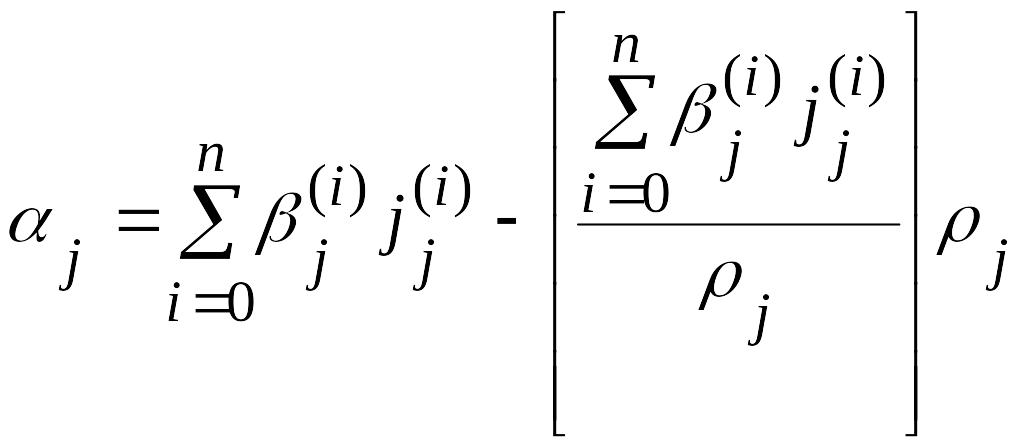, j= 1, 2, … , m. (3.16)

Здесь 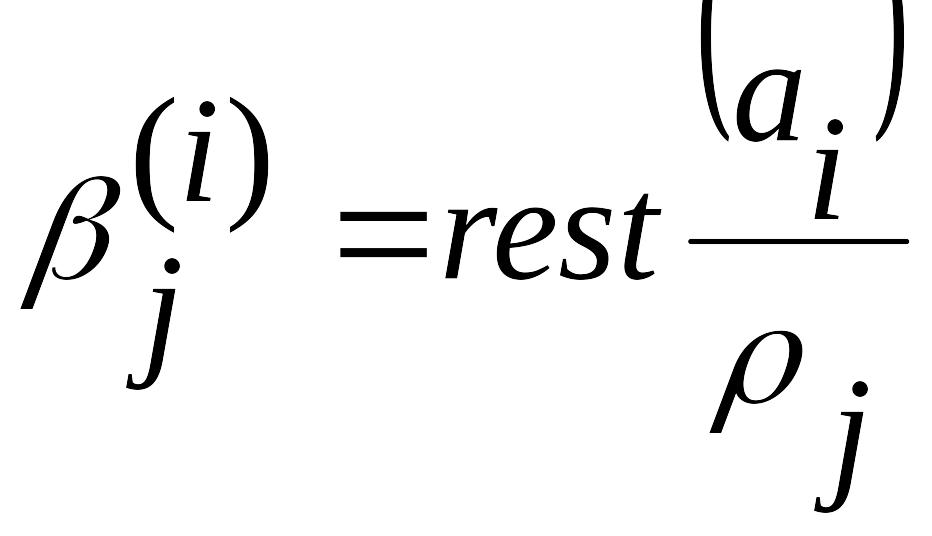, 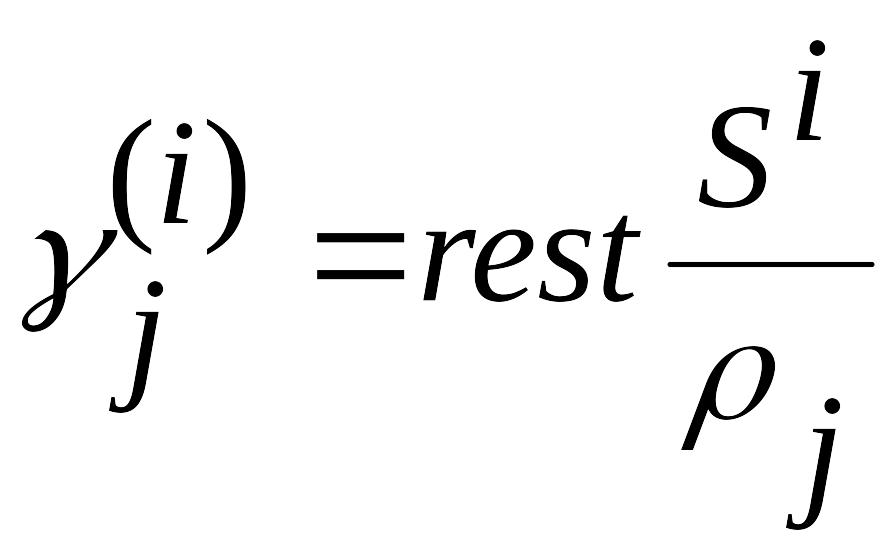. (3.17)

Формула (3.16) наиболее часто записывается еще в виде

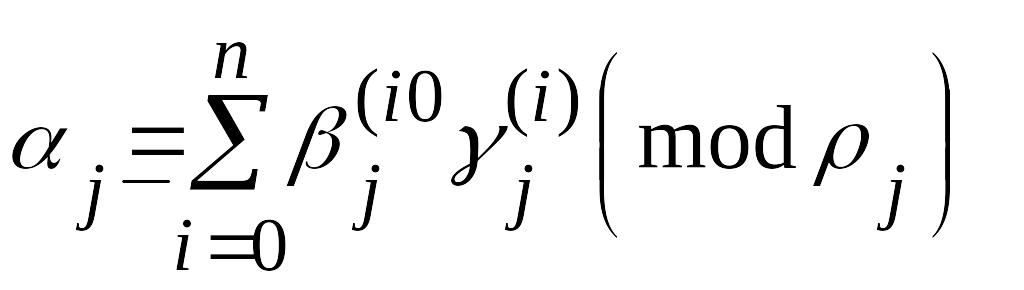, j= 1, 2, … , m , (3.18)

где символ = означает сравнимость левой и правой частей выражения (3.18) по модулю или, другими словами, одинаковость их остатков при делении на этот модуль.

Таким образом, выполняя по формуле (3.16) арифметические действия в ССОК, можно легко найти , j= 1, 2, … , m, если известны ,

k=0,1, …, S-1, и 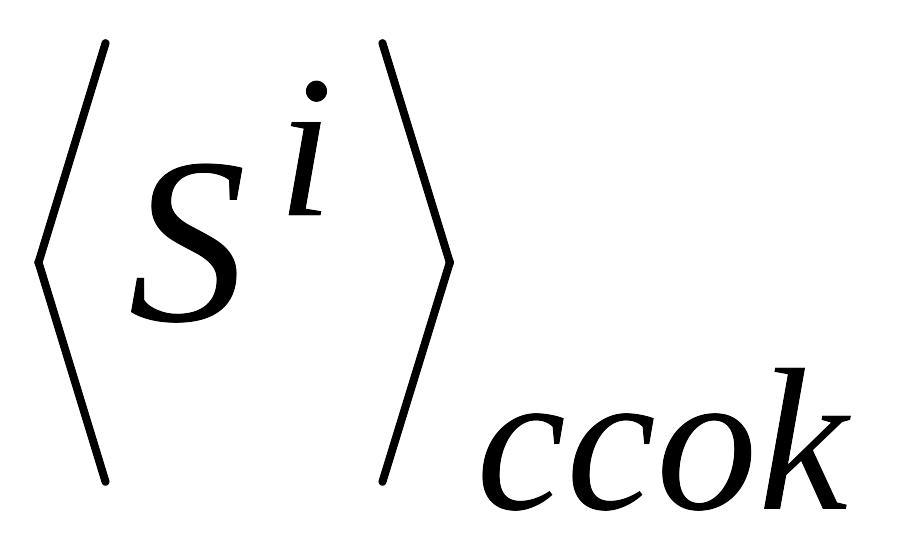, i= 0, 1, …, n. Число констант можно уменьшить, имея в виду следующее.

Как следует из (3.17) , 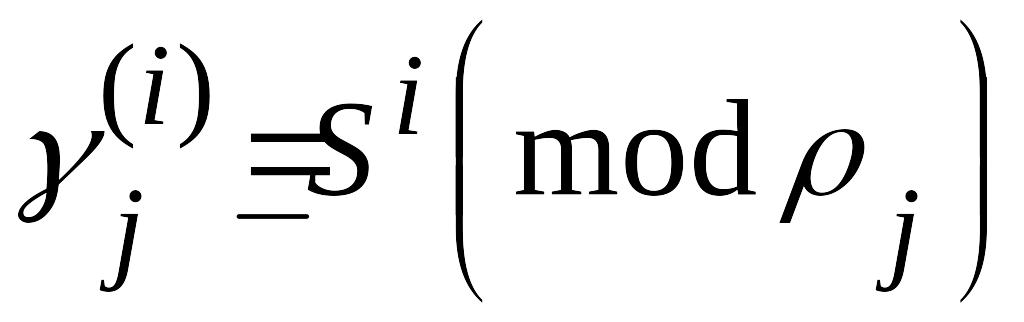, откуда

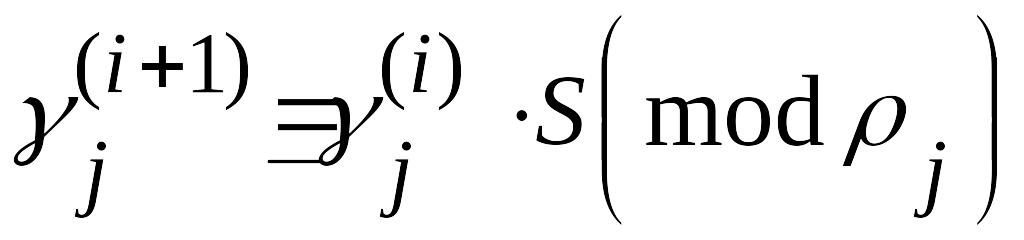. (3.19)

При любом . Остальные , i=1, 2, …, n, легко находятся с помощью соотношения (3.19). Нетрудно заметить также, что последовательность значений , i=1, 2, …, n, начиная с некоторого i, как правило, повторяется, что существенно облегчает подсчет этих значений.

Цифры ССОК в процессе преобразования кодируются или в исходной, или в какой-либо другой системе счисления. Преобразование особенно упрощается, если S=2, поскольку в этом случае 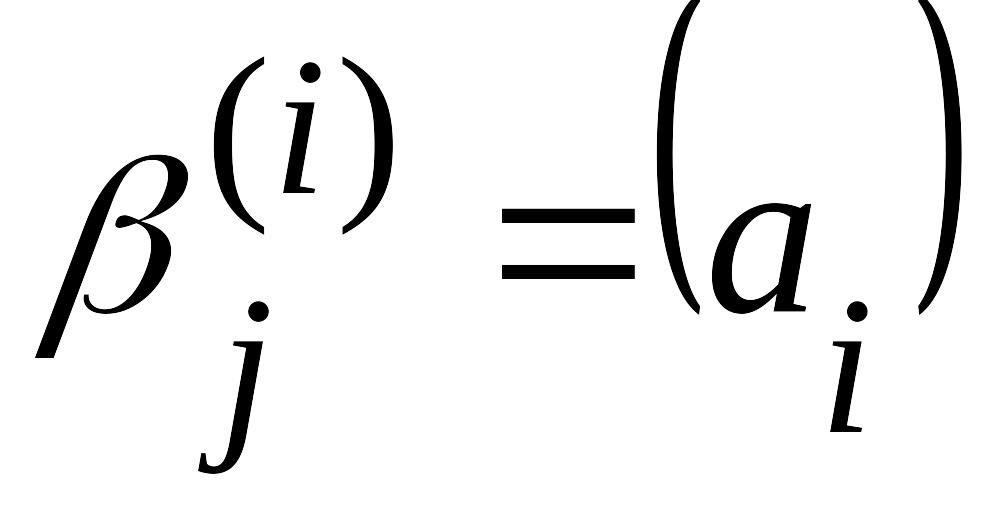(при любом ).

Пусть, например, =1011011;

Преобразование также выполним в двоичной системе счисления. По формулам (3.18) и (3.19) находим

т.е.

Следовательно,

Можно, конечно, избавиться от умножения при преобразовании, используя константы 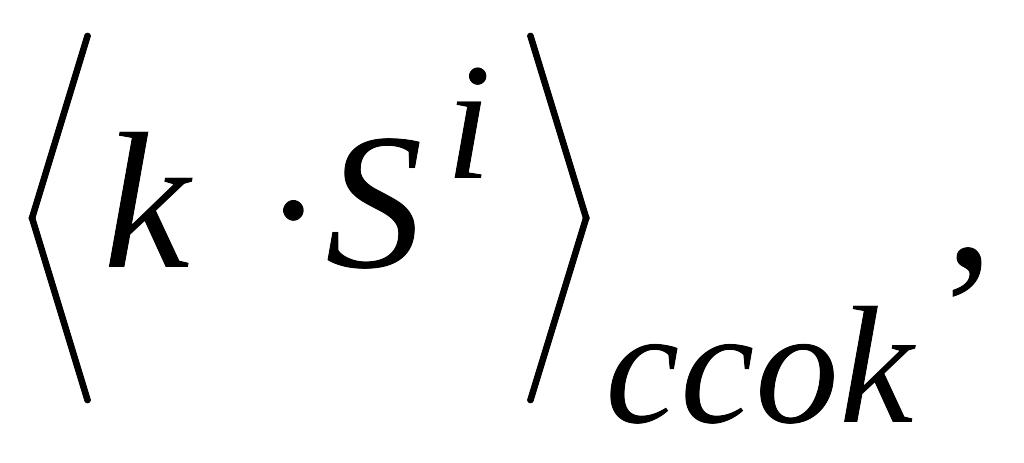k=0,1,…,S-1; i=0,1,…,n. Это позволяет повысить скорость преобразования, однако одновременно возрастают и потребности в машинной памяти.

Преобразование же по методу непосредственного деления x на основания с целью получения остатков , как это вытекает из определения ССОК, практически не применяется в ЭВМ из-за его громоздкости.

3.2.3.2. Рассмотрим теперь задачу обратного преобразования при прочих равных условиях. Предположим также, что нам известны некоторые числа , называемые базисами ССОК, причем

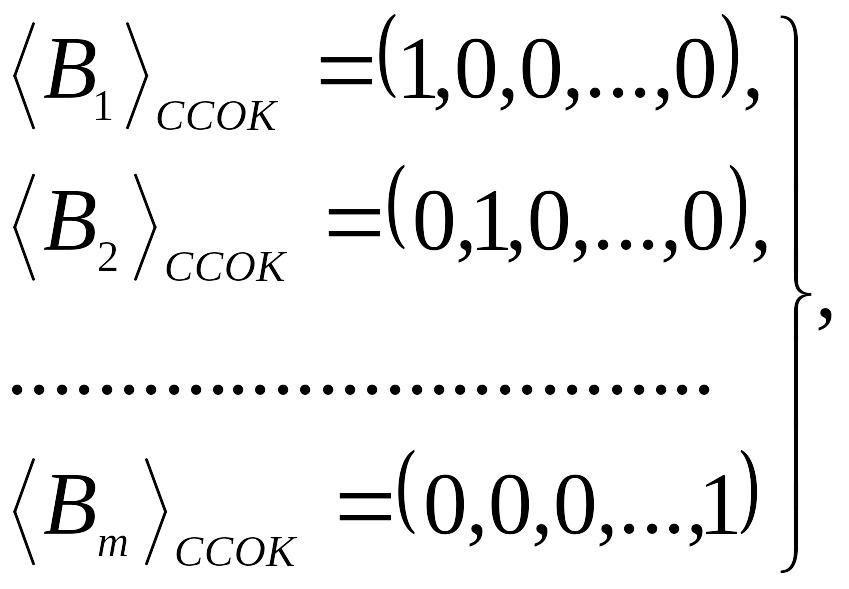(3.20)

т.е. базисы являются ортогональными.

Ясно, что в этих условиях

(3.21)

а , j=1,2, …, m, (3.22)

где

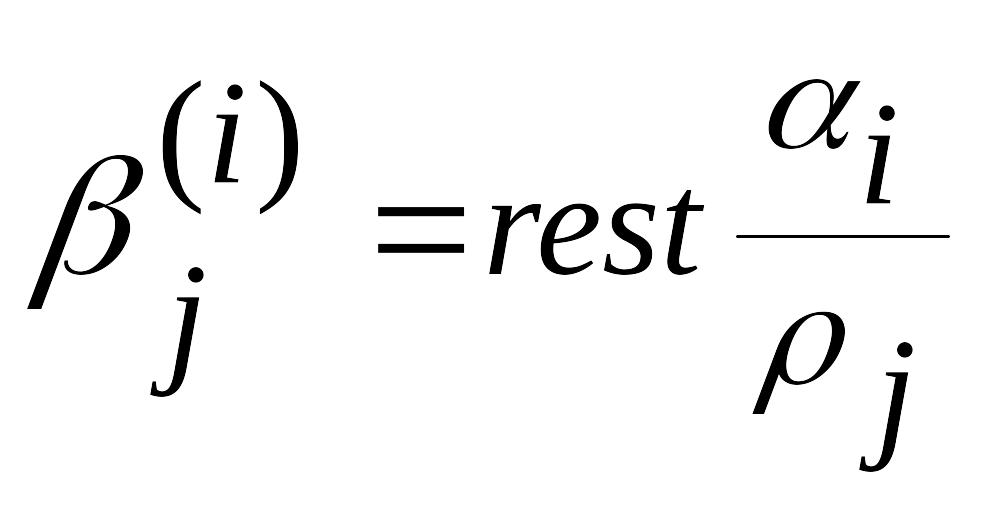, . (3.23)

Сопоставляя (3.22) с (3.18), а (3.23) с (3.17), видим, что (3.21) представляет собой запись в ССОК выражения

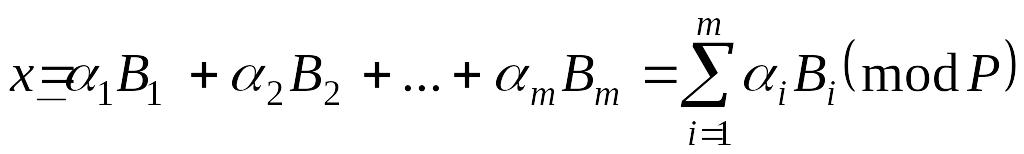, (3.24)

вид которого эквивалентен (3.15).

Если и заданы в системе с основанием S, то реализация (3.24) в этой системе дает непосредственно. В противном случае необходим перевод результата подсчета по формуле (3.24) из системы, в которой представлены и , в требуемую систему счисления.

В соответствии с (3.20) ортогональные базисы могут быть представлены в виде

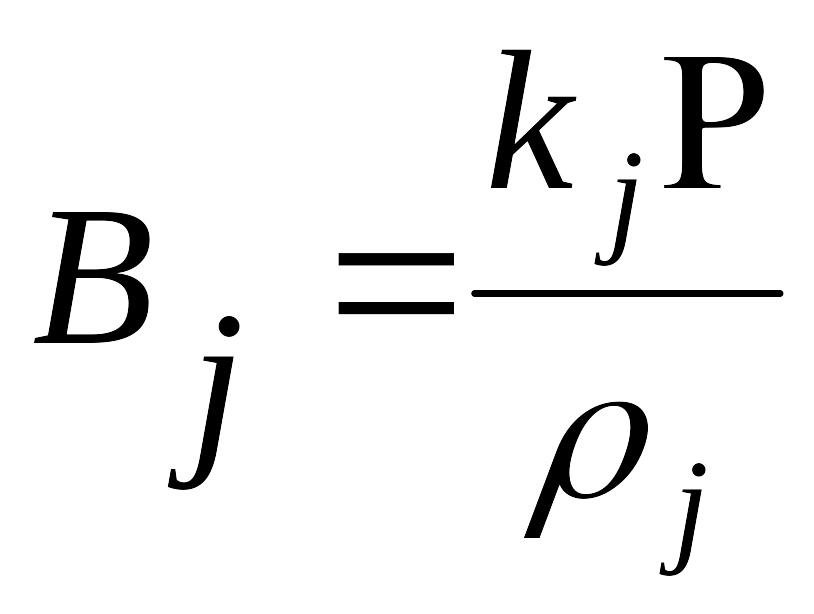, j= 1, 2, … , m ,

где - наименьшее целое положительное число, называемое весом базиса и обеспечивающее =1 при i=j. Величина определяется следующим образом. Вначале находится величина 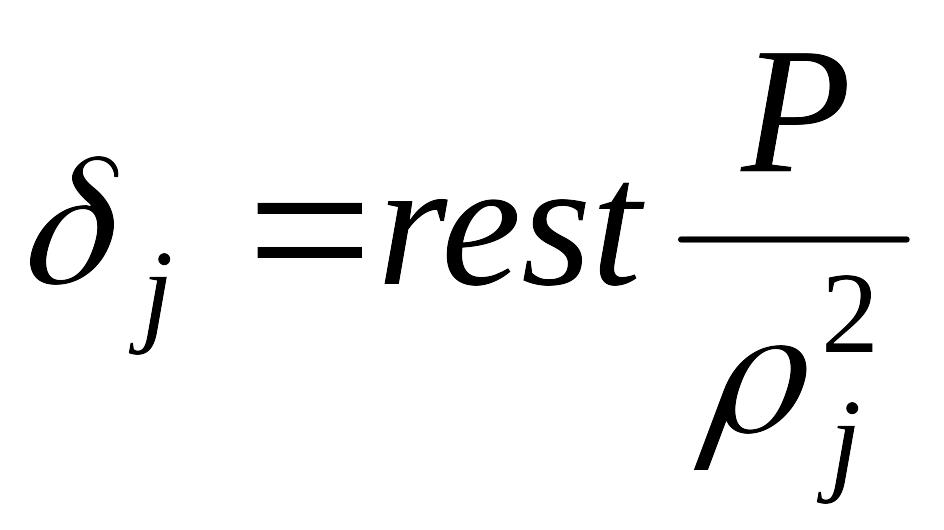, а затем , как результат решения сравнения

, (3.25)

поскольку, как это следует из (3.20),

.

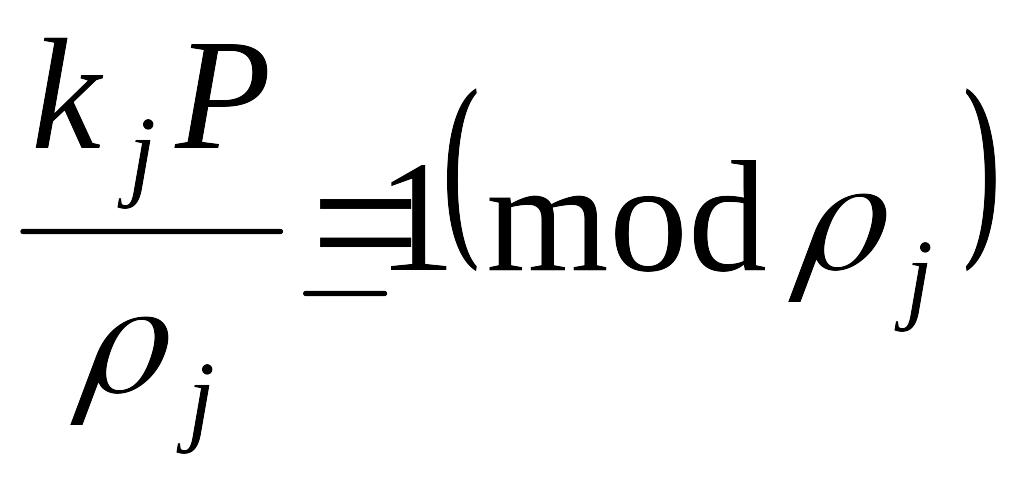Величины для некоторых возможных значений и приведены в табл.3.14.

3.14

(3.25)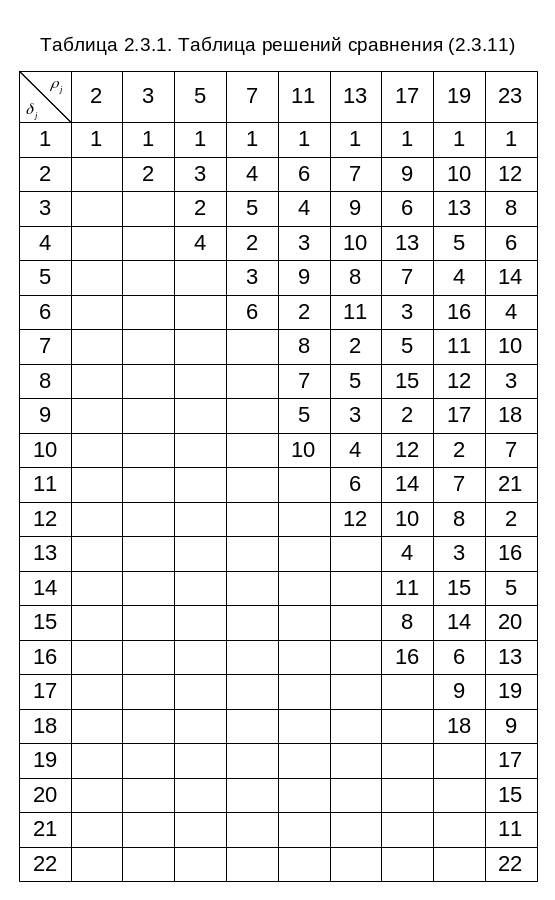

Пусть, например, =(2,1,5,4), =3, =5, =7, =17.

Найдем . Имеем =1, =2, =3, =3. Тогда по табл. 3.14 получим =1, =3, =5, =6. Следовательно, =595, =1071, =1275, =630. Подставляя и полученные значения , i=1,2,3,4, в (3.24), найдем

( 1785),

т.е. =446.

Другие алгоритмы преобразования описаны в работе [3.1 ].