3.2. Перевод чисел из одной системы счисления в другую
1.3.6Перевод чисел из одной естественной системы счисления в другую
Обозначим символом
S
основание исходной системы, а символом
S
-
основание системы, в которую число x
необходимо перевести. Предположим
вначале, что S
и S
являются натуральными, а x – целым.
3.2.1.1. Перевод по методу непосредственной замены в этом случае сводится к реализации соотношения: (3.9)
где
- код количества x в системе счисления
с основанием S ;
-
цифры системы с основанием
,i
=0,1,…,n;
( ) – количественный эквивалент цифры в нулевом разряде этой системы;
- цифры системы с
основанием
,
j=0,1,…,k.
Так, к примеру,
Как видим, при
такой замене необходимо помнить
представление всех компонент
в системе с основанием
и уметь выполнять в этой системе
арифметические действия. Следовательно,
этот метод удобен, когда
-
основание привычной для нас системы
счисления.
3.2.1.2. При табличном методе перевода предварительно составляется таблица вида табл. 3.12.
3.12
В нижней строке
ее фиксируется результат перевода,
процедура которого во многом напоминает
процедуру взвешивания. Эталонами веса
здесь являются числа, представленные
в исходной системе и находящиеся в
клетках таблицы. Первоначально выбирается
такое из этих чисел, которое равно
или
наиболее близко к нему. Тем самым
определяется номер старшего значащего
разряда k и цифра
кода
.
Далее находится разность
,
по которой на следующем шаге отыскивается
новая значащая цифра, и т. д.
Взвешивание прекращается на некотором шаге, если получаемая в конце его разность равна нулю. В оставшихся разрядах целой части , если таковые имеются, записываются нули.
Поясним рассмотренный
метод на примере перевода кода
в
двоичную систему счисления. Соответствующая
таблица будет иметь вид, в ней же приведен
и результат перевода:
Легко понять, что этот метод удобен, когда S - основание привычной для нас системы счисления. Число столбцов составляемой таблицы определяется максимальной разрядностью кода .
3.2.1.3. Для перевода целых чисел широко используется также метод деления, заключающийся в следующем. Запишем результат перевода в виде
.
Очевидно, что
(3.10)
Разделим левую и
правую часть (2.1.2) на
.
При этом
, (3.11)
а наименьший
положительный остаток будет равен
.
Другими словами, мы получаем в остатке
в результате этого деления цифру
в
-ичной записи. Легко видеть из (3.11), что
при делении
на
в остатке будет получена
-ичная запись цифры
и т.д. Это позволяет сформулировать
следующее правило перевода целых чисел
по методу деления:
- найти
;
- проверить не
равно ли частное
нулю; если нет, то вернуться к предыдущему
пункту, заменив
на
, и т.д.;
- при получении
частного, равного нулю, выписать все
полученные ранее остатки в порядке,
обратном порядку их получения, заменив
их цифрами
-ичной системы, если это необходимо.
Найденная запись есть
.
Пусть, к примеру,
.
Тогда
Следовательно,
.
Как видим, метод деления особенно удобен, когда исходная система счисления является привычной для человека.
Рассмотрим теперь
при неизменных прочих условиях задачу
перевода дробных чисел. Ясно, что о
точном переводе здесь уже говорить не
приходится, поскольку конечная
-ичная
дробь может не иметь конечного
-ичного
представления. Поэтому перевод, как
правило, осуществляется с некоторой
заранее заданной точностью
,
задаваемой обычно в виде некоторой
отрицательной степени
,
т.е.
=
,
где l – целое число.
При переводе дробных чисел, также как и при переводе целых чисел, можно воспользоваться методом непосредственной замены и табличным методом. При этом соотношение (3.9) принимает вид
а табл.3.12
трансформируется в табл.3.13. Здесь
и
- цифры
-ичной
и
-ичной
систем соответственно, i = -1, -2, … , -m; j =
-1, -2, …, -l. Все отмеченные выше достоинства
и недостатки этих методов справедливы
и в рассматриваемом случае.
3.13
3.2.1.4. Однако наиболее часто при переводе дробных чисел используют метод умножения. Запишем результат перевода в виде
Ясно, что
(3.12)
Умножим левую и
правую части (3.12) на
.
Получим
и дробную часть, равную
Вновь умножая
последнюю на
,
получим в качестве новой целой части
и т.д. Другими словами, в процессе
умножения дробных частей в качестве
целых частей получаются
-ичные
представления цифр
,
, … .
Это позволяет сформулировать следующее правило перевода дробных чисел по методу умножения:
- найти ;
- возвратиться к
предыдущему пункту, заменив
на дробную часть произведения
;
- закончить перевод,
выполнив l повторений первого пункта,
если точность перевода
=
;
выписать найденные в процессе перевода
целые части в порядке их получения,
заменив их цифрами
-ичной
системы, если это необходимо; найденная
запись есть
.
Пусть, к примеру,
=10,
=15,
=0,17,
=
.
Тогда
2,55;
8,25;
3,75;
11,25;
3,75.
Следовательно,
,
где
- цифра с количественным эквивалентом
в нулевом разряде, равным 11.
Легко понять, что метод умножения наиболее удобен, когда исходная система счисления привычна для человека.
При переводе смешанного числа целая и дробная его части переводятся отдельно, как это было изложено выше, а затем полученные коды объединяются в общую запись.
Рассмотрим теперь
частный случай перевода чисел из одной
системы счисления с натуральным
основанием в другую, когда
,
где r - целое положительное число.
3.2.1.5. Справедливо
следующее утверждение. Для перевода
любого числа x из системы счисления с
основанием
в
систему с основанием
необходимо заменить каждую цифру в коде
её
r-разрядным
-ичным
кодом.
Действительно,
если
,
то как следует из соотношения (3.1),
,
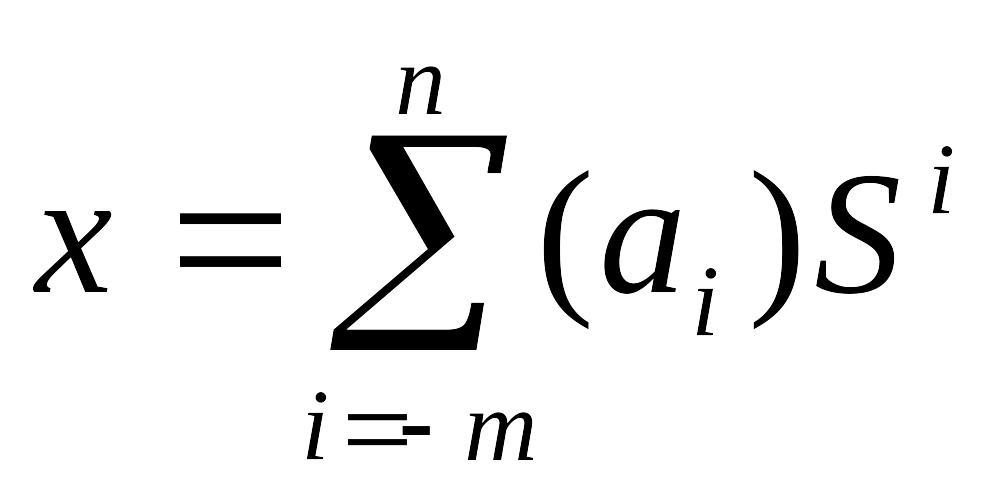причем
.
Замена цифры
соответствующим
ей
-ичным
кодом
позволяет
заменить в этом соотношении её
количественный эквивалент
равным ему эквивалентом (3.13)
,
где
,
(
)
– некоторая
-ичная
цифра и отвечающий ей эквивалент в
нулевом разряде в порядке упоминания,
Подставляя (3.13) в (3.1), найдем, что
.
Положим теперь
.
При i=-m,
=0
j=-rm, а при i=n,
=r-1
j=r(n+1)-1.
Тогда
.
(3.14)
Соотношение (3.14) позволяет смотреть на запись, полученную в результате замены, выполненной в соответствии со сформулированным выше предложением, как на представление числа x в -ичной системе, то есть как на код .
Легко понять также,
что переход от
к
может быть реализован в обратном порядке.
При этом код
следует
разбить влево и вправо от запятой на
группы разрядов по r разрядов в каждой,
а затем заменить упомянутые группы
соответствующими им
-ичными
цифрами.
Так, к примеру,
.
Перейдем далее к вопросу перевода чисел в симметричные и кососимметричные системы счисления. В этом случае переводят первоначально по изложенным выше правилам в смещенную систему с основанием , равным основанию рассматриваемой симметричной или кососимметричной системы, а затем заменяют в полученной записи цифры на цифры требуемой системы, выполняя при необходимости суммирование последних в этой системе. Обратный перевод легко реализуется методом непосредственной замены.
Пусть, например,
надо перевести число
=70,375
в симметричную троичную систему. Это
число в обычной троичной системе имеет
вид
=2121,101
с точностью до
.
Имеем
+
Окончательный
ответ:
.
3.2.1.6.Рассмотрим,
наконец, случай перевода чисел в систему
счисления с отрицательным основанием.
Общий алгоритм такого перевода мы
описывать не будем, а ограничимся лишь
изложением без доказательства правил
перевода в систему с основанием -2. Для
этого исходное число переводится сначала
в обычную двоичную систему счисления.
Далее при
под ним подписывается число, у которого
в каждом четном разряде имеется 1, если
в соседнем справа разряде у
есть
1. Эти числа суммируются по правилам
сложения в минус двоичной системе. При
подписываемое число имеет 1 в каждом
нечетном разряде, если выполняется
аналогичное условие. Знак же
в
процессе минус двоичного сложения
игнорируется.
Так, например, если =-107, то =-110 1011.
Получаем 01101011
+ 10000010
10010101
Следовательно,
=10010101.