Основы алгебры логики

Рис. 4

Наиболее важные теоремы, отражающие основные соот­ношения алгебры логики, приведены в таблице (Рис. 4).

Легко заметить, что все теоремы (кроме 5) представле­ны парой соотношений, каждое из которых получается заменой операций И на ИЛИ, операции ИЛИ на И, логической 1 на логический 0 и логического 0 на логическую 1. Теоремам булевой алгебры присуще свойство сим­метрии, известное как принцип двойственности.

Правильность всех перечисленных теорем легко доказать перебором всех возможностей, т. е. методом совер­шенной индукции. Поскольку переменные в булевой ал­гебре принимают лишь два значения, то число всех возможных комбинаций значений переменных невелико и проверка выполнения теорем для каждой комбинации не является сложной.

Минимизация логических функций

Логическая функция, задающая принцип построения схемы цифрового устройства, может быть, как было пока­зано выше, представлена в виде таблицы истинности или в виде СДНФ или СКНФ и может быть использована для получения логической схемы устройства. Однако получен­ная логическая схема, как правило, не будет оптимальна. Поэтому важным этапом синтеза логических схем являет­ся минимизация логических функций, для чего разрабо­тан ряд методов.

Одним из простых методов минимизации является ме­тод непосредственных преобразований, который осуще­ствляется с использованием основных теорем алгебры логики.

Например, логическую функцию F в виде СДНФ, по­лученную в «Логических функциях и способах их записи», можно минимизировать следующим об­разом:

1. Добавим к данной функции слагаемое х₁•x₂•x₃, ко­торое уже есть в данной функции, используя правило 3 (см. Рис. 4):

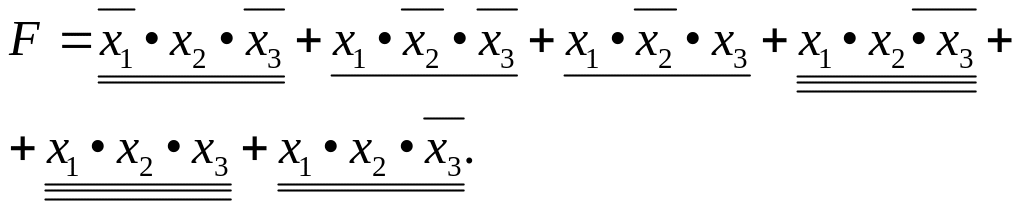
2. П 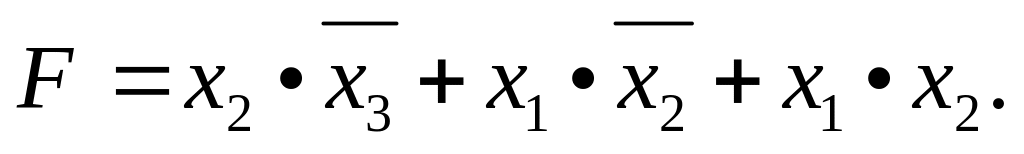рименим метод склеивания (теорема II, рис. 3.26) одинаково подчеркнутых элементарных конъюнкций.

2. Применим метод склеивания для двух последних элементарных конъюнкций

Полученная в результате минимизации логическая функция называется тупиковой. Логическая функция мо­жет иметь несколько тупиковых форм.

Для минимизации логических функций широко ис­пользуется графический метод с помощью карт «Карно» или карт (диаграмм) Вейча, который удобен при неболь­шом числе переменных.

Карты Карно и карты Вейча являются важным сред­ством проектирования логических схем, представляют собой определенную таблицу истинности обычно для двух, трех и четырех переменных и отличаются друг от друга способом обозначения строк и столбцов таблиц ис­тинности. На рис. 5 представлены карты Вейча для двух, трех и четырех переменных соответственно.

Рис. 5

1	1
1	0

Расположение групп переменных х, не имеет значения, необходимо лишь, чтобы каждая клетка отличалась от любой соседней лишь на одну переменную. Согласно при­нятой форме построения карт соседними также считают­ся клетки первой и последней строк, клетки первого и последнего столбцов. Число клеток карты равно числу возможных комбинаций значений переменных и в каждую клетку записывается значение логической функции, соот­ветствующее данному набору переменных. Этот набор пе­ременных определяется присвоением значения логичес­кой 1 переменным, на пересечении строк и столбцов которых расположена клетка.

Например, если логическая функция задана таблицей истинности (рис. 6(а)), то карта Карно для нее будет иметь вид, показанный на рис. 6(б).

а) б)

X1	X2	F
0	0	0
0	1	1
1	0	1
1	1	1

Рис. 6 Булево выражение данной функции имеет вид

Но для упрощения функции можно использовать и карты Карно, в которых логические 1, записанные в со­седних клетках, обозначают, что соответствующие этим 1 конъюнкции (произведения) отличаются лишь по одной переменной, которые дополняют друг друга и их можно опустить.

Т ак в первой строке карты Карно (см. рис. 6(б)) пе­ременная х₁ встречается в комбинации с x₂ и , которые дополняют друг друга:

Таким образом, группируя две соседние клетки в верх­ней строке (контур на рис. 6(б)), можно исключить одну переменную и получить упрошенное выражение - x₁.

А налогично, группируя две соседние клетки в левом столбце (контур на рис. 6(б)) и исключая отличающие­ся переменные (x₁ и х₁), получим упрощенное выраже­ние — х₂.

Полученные упрощенные выражения объединяют с помощью операции ИЛИ.

Таким образом, упрощенное выражение логической функции будет иметь вид

Таким образом, соседние клетки карты Карно можно группировать для исключения переменной. Число группи­руемых клеток может быть и больше двух, но их число должно быть четным и они должны соприкасаться (яв­ляться соседними) друг с другом.

Допускается также иметь несколько групп перекрываю­щихся клеток, как в только что рассмотренном примере.

Группироваться могут также клетки первой и послед­ней строк, первого и последнего столбцов, т. е. карту до­пускается сворачивать в цилиндр, как по вертикальной, так и по горизонтальной оси.

Для исключения n переменных общее число группиру­емых клеток должно быть равно 2ⁿ. Так, для исключения одной переменной требуется объединить две соседние клетки, а для исключения трех переменных уже требует­ся объединить восемь соседних клеток.

Таким образом, для того чтобы получить минимизиро­ванную логическую функцию, необходимо сгруппировать все соседние клетки карты Карно, содержащие 1, а затем объединить полученные группы с помощью операции ИЛИ. Клетки, содержащие 1, которые не удалось объеди­нить с другими клетками, образуют в минимизированной логической функции самостоятельные члены, каждый из которых содержит все переменные.

Р ассмотрим несколько примеров карт Вейча и спосо­бы построения контуров группировки соседних клеток для получения упрощенной логической функции. Так, карта Вейча для логической функции

п риведена на рис. 7

0	0	0	0
1	0	0	1
1	0	0	1
0	0	0	0

Рис. 7

На этом рисунке показан правильный способ объеди­нения соседних ячеек, т. е. карта Вейча как бы свернута в вертикально расположенный цилиндр.

У прощенное выражение логической функции имеет вид

Таким образом, группируя соседние клетки в единый квадрат, удалось исключить две переменные (x₁ и х₂) и получить простое выражение для логической функции.

Рис. 8

Рассмотрим пример минимизации логической функции

для которой карта Вейча имеет вид рис. 8.

Г руппируемые ячейки обведены двумя контурами. Нижний контур даст возможность исключить одну переменную X₃ и после этого в нем остается член x₁•x₂•x₃. В верхнем контуре можно исключить две переменные (х₂ и x₄) и после этого в нем остается член х₁х₃. Упрошенное булево выражение логической функции имеет вид

Можно объединять в квадрат также четыре угловые клетки карты Вейча, как это показано на рис. 9, кото­рая построена для логической функции

Рис. 9

О бъединенные клетки являются соседними (если по­верхность представить в виде тора), и это объединении позволяет исключить две переменные х₁ и x₂ и получить простое выражение логической функции

Рассмотрим минимизацию логической функции, кар­та Вейча которой представлена на рисунке 10:

Рис. 10

Булево выражение этой функции имеет вид

Ч етыре угловые клетки можно объединить в одну груп­пу, как это делалось в предыдущем примере. Это объеди­нение позволяет исключить две переменные (х₁ и х₂) и получить член х₃• х₄.

Две единицы из первой строки можно объединить с двумя единицами из нижней строки, получить группу из четырех ячеек, которая позволяет исключить две перемен­ные (х₄ и х₃) и получить член

Наконец, единственную оставшуюся единицу (из вто­рой строки и последнего столбца) можно объединить с клеткой, находящейся над ней, и это позволит исключать одну переменную (x₄) и получить член

Таким образом, мы получим минимизированную логи­ческую функцию

Следует отметить, что для получения минимальной формы логической функции необходимо группировать наибольшее число клеток, причем некоторые клетки мо­гут входить в разные группы. В зависимости от выбора групп объединения клеток можно получить несколько упрощенных выражений логической функции,

В ряде случаев не все значения логической функции бывают определены однозначно. Например, в некоторых случаях, известно, что какие-то комбинации входных пе­ременных (сигналов на входе логической схемы) появить­ся не могут, или, если они появляются, то значение логи­ческой функции (сигнала на выходе логической схемы) не существенно. В таких случаях говорят о неопределенных условиях, и на карте Вейча такое неопределенное условие может обозначаться прочерком.

Рассмотрим, как карту Вейча с неопределенными ус­ловиями можно использовать для минимизации логичес­кой функции.

Пусть имеется карта Вейча такой функции (рис. 11)

Рис. 11

При минимизации клетки с недоопределенными состо­яниями могут произвольным образом включаться в груп­пы при объединении клеток, причем им может присваи­ваться любое значение (0 или 1) таким образом, чтобы сгруппировать наибольшее число клеток

Т ак, в рассматриваемом примере вместо всех прочер­ков можно проставить логические 1 и получить две боль­шие группы по восемь клеток (два контура на рис. 11), что позволит исключить три переменные и получить сле­дующее упрошенное выражение логической функции:

Если клетки с неопределенными условиями не исполь­зовать, то можно получить две группы по четыре клетки, что позволит получить следующее упрощенное выражение логической функции:

Очевидно, что данное выражение логической функции сложнее предыдущего.

При минимизации логической функции, содержащей более четырех переменных, используются другие способы минимизации.