Министерство
образования и науки Украины
Донецкий
национальный технический университет
Лабораторная
работа №1
Численное
решение уравнений итерационными
методами
Выполнил:
\
ст.
гр. КС-10а
Бородин Богдан
Донецк
2012
Вар. |
аО |
а1 |
а2 |
аЗ |
Eps |
№ корня |
1 |
0,6768 |
-0,144 |
-0,47 |
од |
0,0001 |
1 |
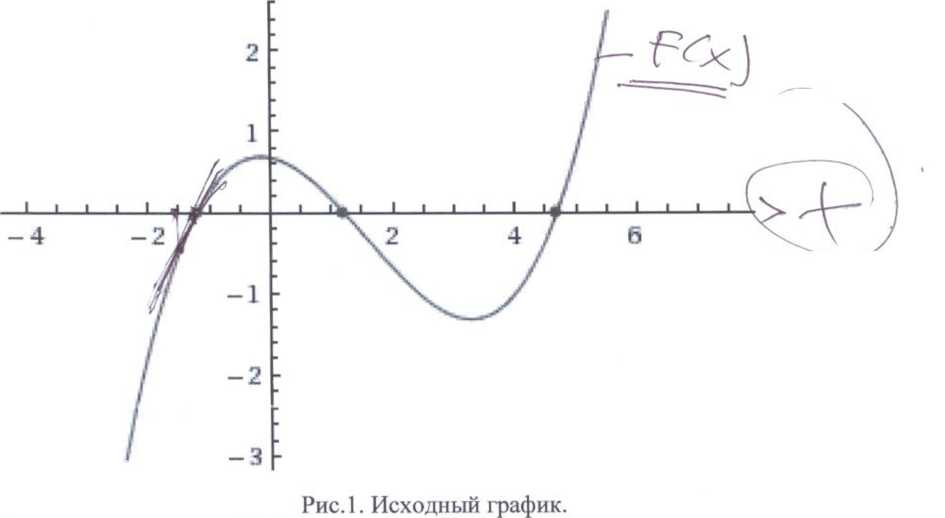
Данная
лабораторная работа посвящена
нахождению корней уравнения4
F(x)
= 0, (1)
где
функция F(x)
может быть алгебраической либо
трансцендентной и должна
удовлетворять
условию дифференцируемости. Как
правило, численное
решение уравнений
состоит из двух этапов: нахождение
приближенного
значения корня
(отделение корня) и уточнение его
значения до заданной
точности.
Начальное приближение часто известно
из физических соображений*
либо
находится специальными методами,
например, графически. Рассмотрим
второй
этап решения уравнении: нахождение
значения корня с заданной
точностью
различными итерационными методами.
Приближенное
значение корня
С
помощью грубого анализа находятся
приближенные значения корней. В
основном
этот анализ сводится к
отысканию таких двух значений х, для
которых F(x)
имеет
противоположные знаки, т.е.
определяются такие х* и х», для которых
F(x*) > 0
и Р(х») < 0.
Тогда между х их. есть
по крайней мере одна точка, где F(x)
= 0.
Зададим
диапазон от х=-10 до х=10. |
У |
-10.000 |
-144.883 |
-9.000 |
-108.997 |
-8.000 |
-79.451 |
-7.000 |
-55.645 |
-6.000 |
-36.979 |
-5.000 |
-22.853 |
-4.000 |
-12.667 |
-3.000 |
-5.821 |
-2.000 |
-1.715 |
-1.000 |
0.251 |
0.000 |
0.677 |
1.000 |
0.163 |
2.000 |
-0.691 |
3.000 |
-1.285 |
4.000 |
-1.019 |
5.000 |
0.707 |
6.000 |
4.493 |
7.000 |
10.939 |
8.000 |
20.645 |
9.000 |
34.211 |
10.000 |
52.237 |
у
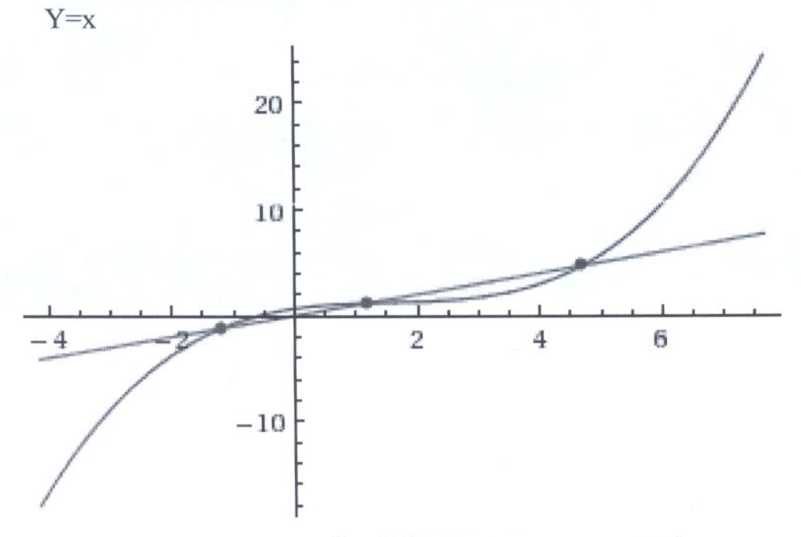
Видно,
что знак меняется на границе х=-2 и х=-1;
х=1 и х-2;
х=4 и х=5.
По
заданию нам необходим корень 1
В
качестве исходного приближения для
нахождения корня F(x)
можно взять:
хо = 1А
(х +х*) = -1,5
Рассчитанное
исходное приближение хо уточняется
четырьмя методами до
достижения
требуемой точности е.
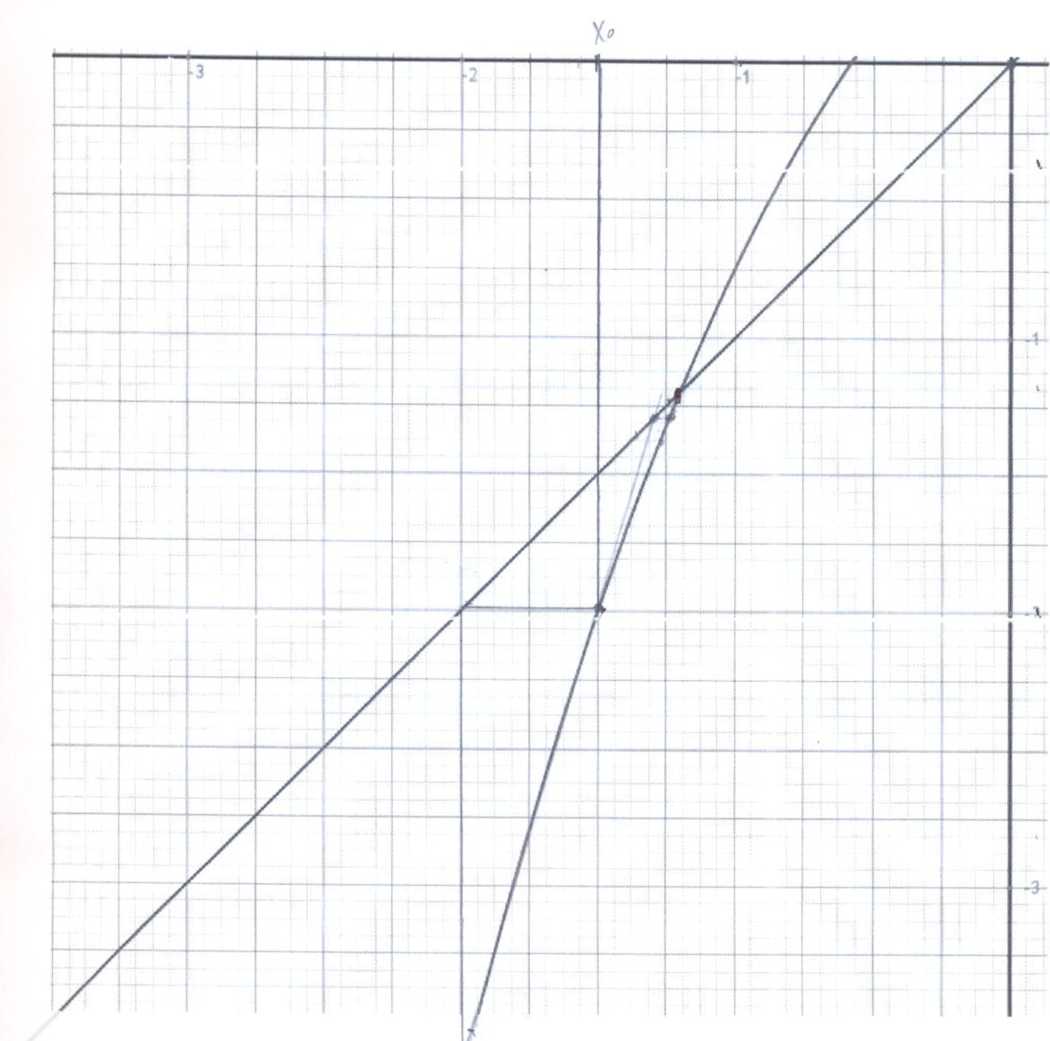
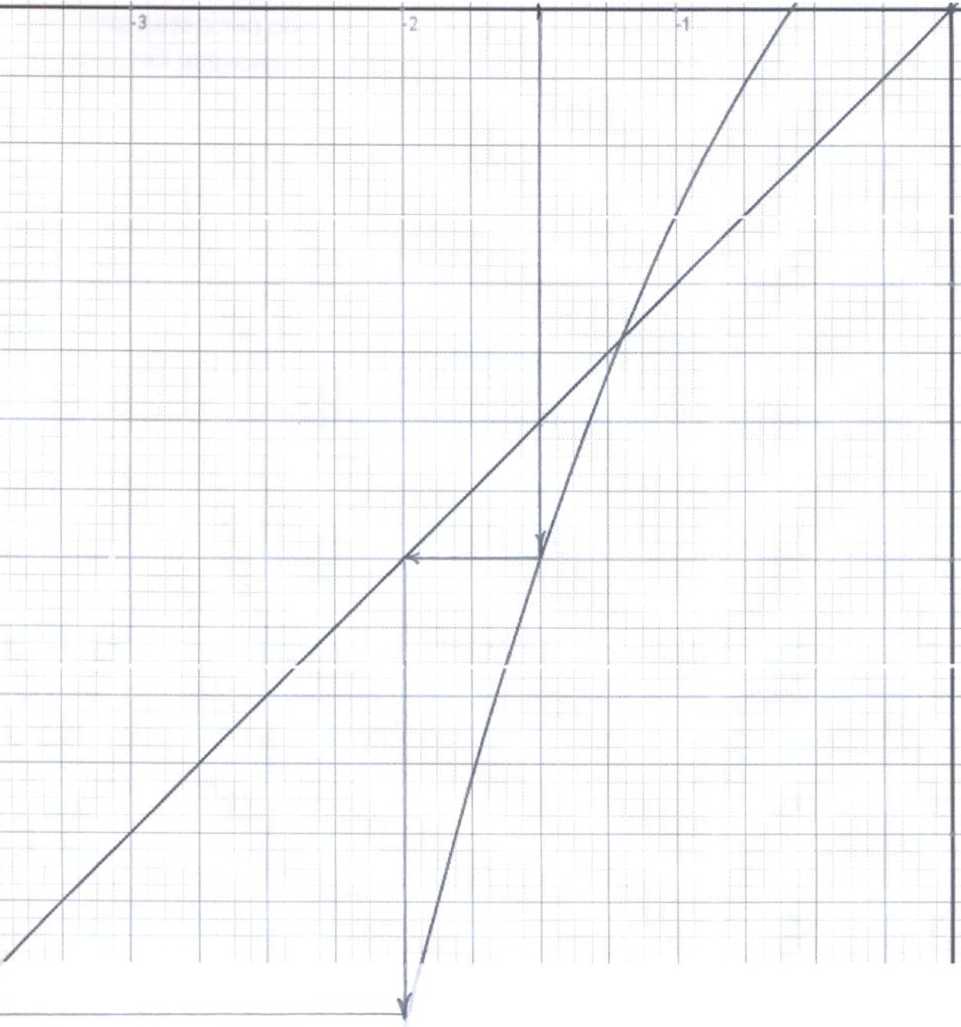
Y^O.6768-0.144*х-0.47*хЛ2+0.1
*хл3
Метод последовательных
приближений
Y=0.6768+(-0.144+1
)*х-0.47*хЛ2+0.1 *хл3=х
Рис.2.
График функции х = / (х).
В
данном методе для удобства вычислений
переводят от исходного
уравнения,
заданного в виде (1), к уравнению
х=/(х).
(2)
Данный
переход можно осуществить множеством
способов, например,
прибавив к обеим
частям (1) х.
Суть
метода последовательных приближений
заключается в том, что
начальное
приближение х0 подставляется в
правую часть формулы (2) и
вычисляется
значение хх. Затем полученное
значение Xi снова
подставляется в
правую часть формулы
(2) и вычисляется значение х2 и
т.д. Рабочая формула
метода
последовательных приближений имеет
вид
xn=/(xn-i).
(3)
Вычисления
продолжаются до тех пор, пока не будет
достигнута
заданная точность е,
то есть
I
Хп-Хп.11
<
£ .
(4)
Основной
проблемой при работе с итерационными
методами является
проблема сходимости.
Достаточным условием сходимости
метода
последовательных приближений
является выполнение условия
1/'(х„)1<1
(5)
для всех значений хп.
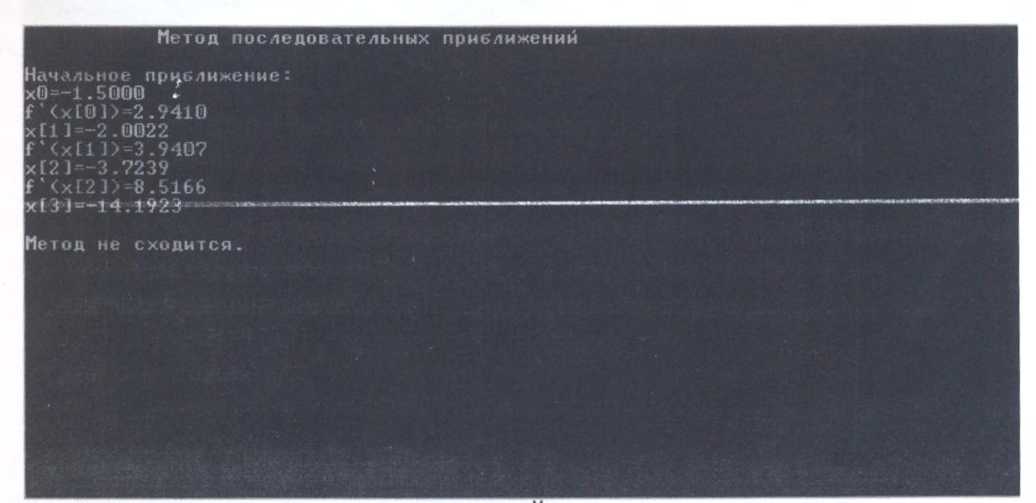
МЕТОД
ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ
Метод последовательных приближений
Формула
данного итерационного метода имеет
вид v
xn+1
= Хп
+ а *( / (Хп)-хп),
(6)
где
а
определяется но формулам
а=1/(1-/Ч#))
(7)
/’(^)
=
(/(Xn)-Xn)/(Xn-Xn-l)
(8)
при
этом на первом шаге хь
определяется простыл методом
последовательных
приближений.
УСОВЕРШЕНДСТВОВАНЫИ
МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ
Небольшая
дальнейшая модификация усовершенствованного
метода
последовательных приближений
приводит к одному из наиболее
известных
численных методов решения
уравнений - методу Ньютона-Рафсона.
Формула
метода для / (х), подчиняющегося
соотношению (2), имеет вид
Хп+1
= ( / (хп)-хп*
/' (хп))/(1-
/' (хп)),
(9)
при этом сходимость метода
обеспечивается, если
х0
выбрано достаточно близко к решению
х =/ (х);
производная
/"(х)
не
становится слишком большой;
производная
/'(х) не слишком близка к 1.
Формула
Ньютона-Рафсона для F(x),
подчиняющегося соотношению (1),
имеет
вид
xn+,
= xn-F(xn)
/ F'(xn),
(10)
при этом условия сходимости
принимают следующий вил:
х0
выбрано достаточно близко к корню
уравнения F(x)=0;
производная
F"(x)
не становится слишком большой;
производная
F'(x)
не слишком близка к 0.
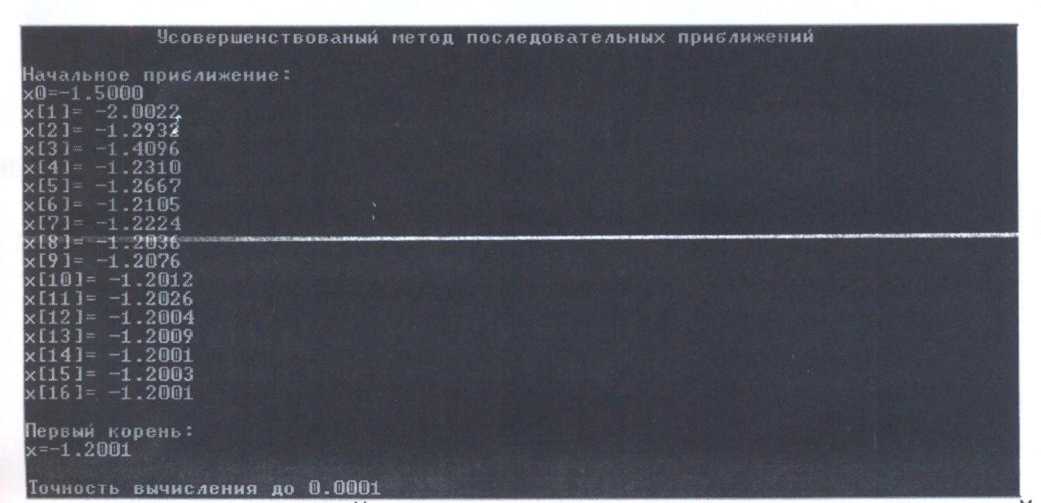
Усовершенствованный метод последовательных приближений
Метод Ньютона-Рафсона

МЕТОД
НИЬЮТОНА-РАФСЛОСА
Данный метод
позволяет находить корни уравнения в
случае, когда F(x)
представляет
собой многочпен степени m
F(x)
= ао + aix + а2х2
+ ... + amxm
(11)
Применим метод
Ньютона-Рафсона согласно формуле (10),
при этом
вычисление F(x)
будем осуществлять по правилу Горнера
с использованием
рекуррентных
формул:
Ьщ (12)
bj =
aj+XnCj+ь
j =
m-l,
...
, 0
таким образом находим F(x)
= b0.
Р'(х)представляет
собой многочлен степени т-1. Воспользовавшись
для
его вычисления теми же рекуррентными
формулами, имеем
cm
= bm
(13)
cj = bj+xnCj+i,
j
= m-1,...,
1
и соответственно F'(x)
= Cj.
Подставляя найденные
значения F(x)
и F'(x) в
формулу (10) для метода
Ньютона-Рафсона,
получаем
xn+i
=хп-Ьо/сь
(14)
где Ь0 и С| вычислены по
формулам (12) и (13).
Выполнение данной
лабораторной работы заключается в
нахождении с
заданной точностью s
одного из корней кубического уравнения
F(x)
= ао + aix + а2х + а3х
= 0
перечисленными выше методами.
Коэффициенты многочлена, точность
вычисления
и номер вычисляемого корня заданы в
таблице. Решение
осуществляется в
два этапа. На первом этапе с помощью
грубого анализа
находятся приближенные
значения корней. В основном этот анализ
сводится к
Метод Бирге-Виетта

отысканию таких
двух значений х, для которых F(x)
имеет противоположные
знаки, т.е.
определяются такие х и х*, для которых
F(x ) > О и
Р(х.) < 0. Тогда
между х и х* есть по
крайней мере одна точка, где F(x)
= 0. В качестве
исходного приближения
для нахождения корня F(x)
можно взять
Х0
= '/2
(х*+х*).
На втором этапе
рассчитанное исходное приближение х0
уточняется каждым из
четырех
рассмотренных методов до достижения
требуемой точности е.
МЕТОД
БИРГЕ-ВИЕТТА
Выводы
В
этой лабораторной работе для численного
решения кубического уравнения
было
предложено четыре итерационных
метода, имеющих разную скорость и
характер
сходимости, различную
степень сложности вычислений для
достижения заданной точности
решения
уравнения.
Для
заданного кубического уравнения по
варианту методы Ньютона-Рафсона и
Бирге-
Виетта показали высокую
скорость сходимости
Метод
прямых приближений не сходится для
заданного корня уравнения.
Усовершенствованный
метод прямых приьлижений сходится за
4 итерации, то есть в
данном случае
почти равен методам Ньютона-Рафсона и
Бирге - Виетта,однако,так бывает
далеко
не всегда
Однако
методы Ньютона-Рафсона и Бирге-Виетта
не могут быть применены, когда
функция
не имеет производной и, кроме того,
имеют большую сложность
арифметических
вычислений, чем
методы прямых приближений, которые
сходятся за большее число
итераций
метода. Поэтому эти методы скорее
дополняют друг друга. Выбор
метода
определяется видом функции,
численное решение которой необходимо
найти.
Важным
преимуществом всех итерационных методов
является то, что ошибка
приближения
не накапливается, а происходит на
последнем этапе расчетов.

Текст
программы:
ttinclude
<stdio.h>
#include <conio.h>
ttinclude <math.h>
void intro();
void parti();
void part2 ();
void part3 () ;
void part4 ();
const float Eps=0.0001;
float a0=0.67
68,al=-0.144,a2=-0.47,a3=0.1;
float k=-10,x[21],xO,*y;
//—
void main ()
{char ch;
printf("Лабораторная
работа
№l\n");
printf("Выполнил:\n");
printf("Бородин
Богдан\п");
printf("Нажмите
Enter...\n");
do
{
do
{
}
while
(getch()
intro();
clrscr();
printf("\n
printf(" {2}
приближений\п");
{1}. Метод
последовательных приближений\п");
Усовершенствованый
метод последовательных
Метод
Ньютона-Рафсона\п")
Метод
Бирге-Виетта\п");
Выход.\п");
parti();break;
part2();break;
part3();break;
: part4();break;
exit(0);
printf(" {3}. I
printf (" {4 } . !
printf(" {5}. :
ch=getch{);
switch(ch)
{
case '1' : p^
case '2'
: ]
case
'31
: ]
case
' 4 ' :
case '5' : <
}
}
while (1) ;
}
II—
void parti()
{float xa,fx;
int
i,j=0;
clrscr();
printf(" Метод
последовательных приближений\n"]
printf("ХпНачальное
приближение:\nx0=%6.4f\n",xO);
xa=xO;
for (i=l;i<4;i++)
{
fx=(a1+1)+2*(a2*xa)+3*(a3*pow(xa,2));
printf("f'(x[%d])=%6.4f\n",j=i-l,fx);
xa=aO+(al+1)*xa+a2*pow(xa,2)+a3*pow(xa,3);
printf("x[%d]=%6.4f\n",i,xa);
}
printf("ХпМетод
не сходится.");
}
//—
void part2()
{float x, xa,fx,a,fs;
int
i=l;
clrscr ();
printf(" Усовершенствованый
метод последовательных
приближений\n");
printf("ХпНачальное
приближение:\nxO=%6.4f\n",хО);
xa=aO+(a1+1)*x0+a2*pow(xO,2)+a3*pow(xO,3);
printf("x[%d]=
%6.4f\n",i,xa);
i++;
x=xO;
do
{
fx=aO+(al+1)*xa+a2*pow(xa,2)+a3*pow(xa,3);
fs=(fx-xa)/(xa-x);
x=xa;
a=l/(1-fs);
xa=xa+a*(fx-xa);
if
(fabs(xa-x)<Eps)
{
printf("\пПервый
корень:\n");
printf("x=%6.4f\n",xa);
printf("ХпТочность
вычисления до 0.0001");
break;
}
printf("x[%d]=
%6.4f\n",i,xa);
i++;
}
while (1) ;
}
II—
void part3()
{float x,xa,fx,fs;
int
i=l;
clrscr();
printf(" Метод
Ньютона-Рафсона\п");
printf("ХпНачальное
поиближение:\nx0=%6.4f\n".xO);
xa=x0;
do
{
fx=a0+al*xa+a2*pow(xa,2)+a3*pow(xa,3);
fs=al+2*(a2*xa)+3*(a3*pow(xa,2));
x=xa;
xa=xa-fx/fs;
if
(fabs(xa-x)<Eps)
{
printf("\пПервый
корень:\n");
printf("x=%6.4f\n",xa);
printf("ХпТочность
вычисления до 0.0001");
break;
}
printf("x[%d ] =
%6.4f\n",i,xa);
i++;
}
while(1);
}
//—
void part4 () «
{float bO,cl,xa,x;
int
i=l;
clrscr ();
printf
(" Метод Бирге-Виетта\п");
printf("ХпНачальное
приближение:\nx0=%6.4f\n",x0);
xa=xO;
do
{
b0=a0+al*xa+a2*pow (xa, 2)
+a3*pcv: (xa, 2) ;
cl=al+2*(a2*xa)+3*(a3*pow(xa,2));
x=xa;
xa=xa-bO/cl;
if
(fabs(xa-x)<Eps)
{
printf("\пПервый
корень::\n");
printf("x=%6.4
f\n",xa);
printf("\пТочность
вычисления до 0.0001");
break;
}
printf("x[%d]=
%6.4f\n",i,xa);
i++;
}
while(1) ;
}
II—
void intro () '
{int i;
for (i=0;i<21;i++)
{
x[i]=k;
k++;
printf("x[%d]=%6.4f
",i,x[i]);
}
printf("\n\n");
y=(float
*)malloc(21*sizeof(float));
for (i=0;i<21;i++)
{
y[i]=a0+al*x[i]+a2*pow(x[i],2)+a3*pow(x[i],3);
printf("y[%d]=%6.4f ",i,у[i]);
}
printf("\n\n");
k=-l
;
for (i=0;i<21;i++) »
{
if
(((y[i]>0)&&(y[i+l]>0))||((y[i]<0)&&(y[i+1]<0)))
{}
else
k++;
if (k==0)
{
x0=(x[i]+x[i+1])/2.0;
break;
}
}
free(y); }