МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра физики

РАСЧЕТ ПОЛИТРОПНЫХ ПРОЦЕССОВ

СМЕСИ ИДЕАЛЬНЫХ ГАЗОВ

Методические указания и задания для выполнения контрольной работы

№ 1 по дисциплине “Теплофизика”

Йошкар-Ола 2012

КОНТРОЛЬНЫЕ ЗАДАНИЯ_ТТД

В объем контрольных заданий входит 4 задачи.

1. Контрольная задача № 1

Провести расчет двух последовательно протекающих процессов изменения состояния смеси идеальных газов и изобразить эти процессы в Р,v– и T,s– диаграммах.

Исходные данные:

1. Состав смеси (химические формулы трех компонентов смеси идеальных газов).

2. Массовая или объемная доля одного из компонентов смеси.

3. Одна из характеристик смеси газов: молекулярная масса смеси, газовая постоянная смеси, изохорная или изобарная теплоемкости смеси.

4. Некоторые термические параметры в начальном и конечном состоянии каждого из указанных процессов или одна из характеристик процесса (показатель политропы, теплота процесса, работа изменения объема, изменение внутренней энергии, энтальпии).

Варианты задания приведены в табл. 1.1 и 1.2.

Таблица 1.1

Исходные данные для расчета характеристик смеси идеальных газов

№	Состав смеси	Доля одного из компонентов	Одна из характеристик смеси
1	2	3	4
1	CH4, CO2, N2	= 0,3	см = 30 кг/кмоль
2	CO2, O2, C2H2	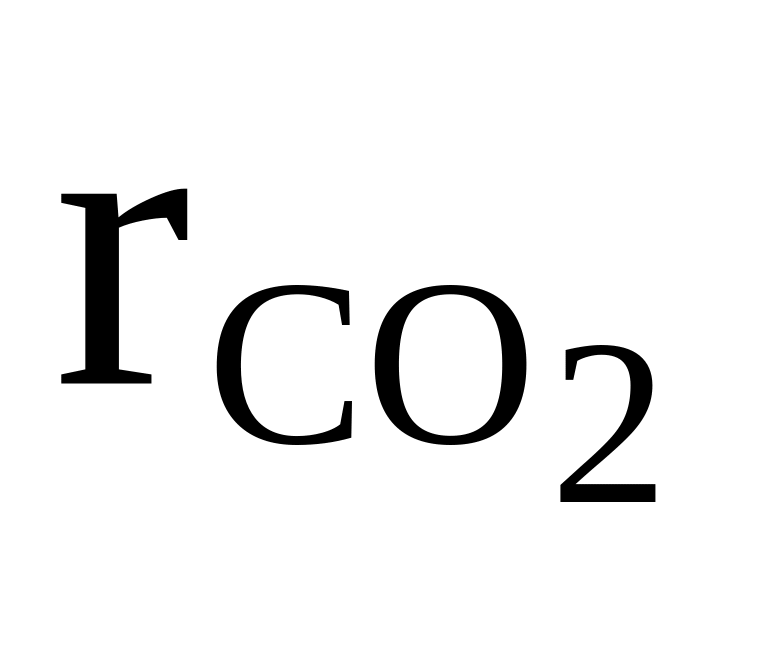= 0,4	cр,см = 31500 Дж/(кмольК)
3	NH3, N2, C2H2	= 0,3	cv,см = 23000 Дж/(кмольК)
4	NH3, SO2, CO	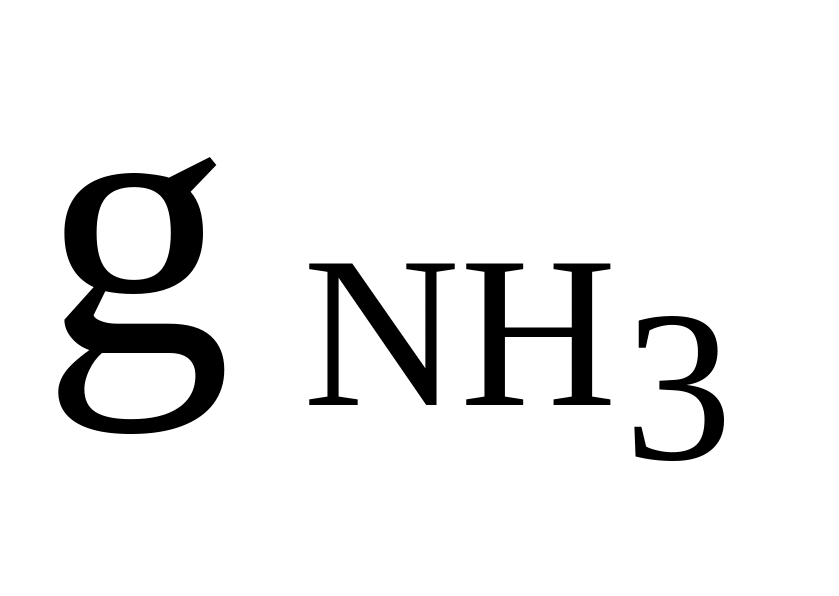= 0,2	Rсм = 280 Дж/(кгК)
5	CO, CH4, O2	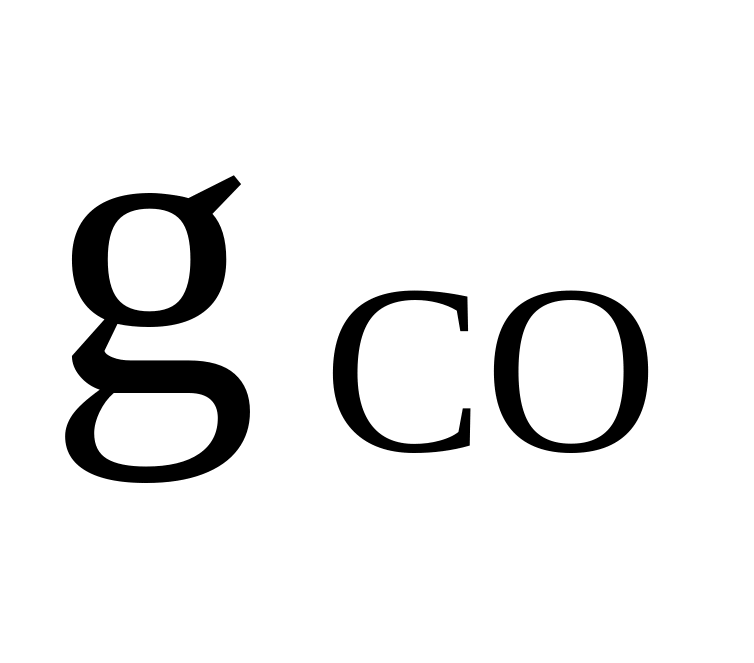= 0,35	cр,см = 1500 Дж/(кгК)
6	CH4, C2H6, N2	= 0,15	cv,см = 900 Дж/(кгК)
7	CO, CH4, O2	= 0,25	см = 25 кг/кмоль
8	C2H6, CO2, N2	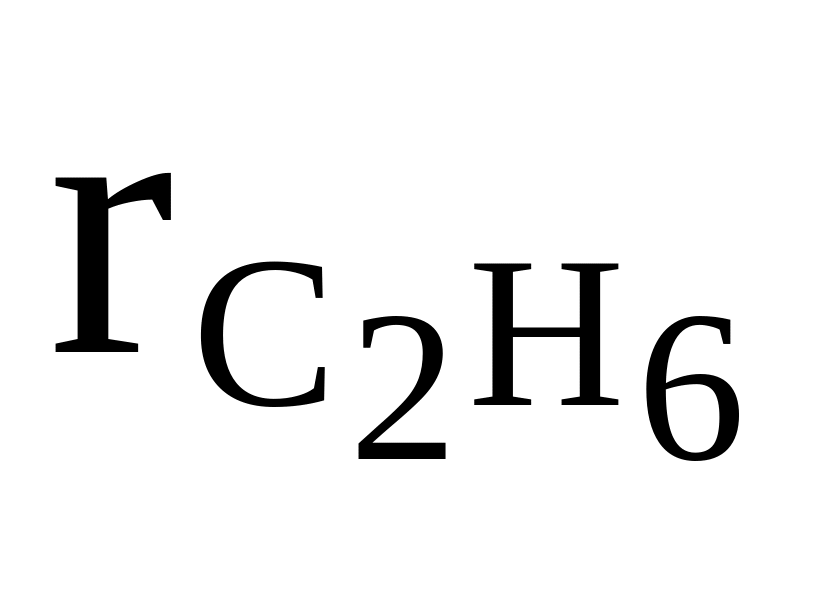= 0,4	cр,см = 32000 Дж/(кмольК)
9	Ne, NH3, N2	= 0,45	cv,см = 18000 Дж/(кмольК)
10	CO2, O2, CO	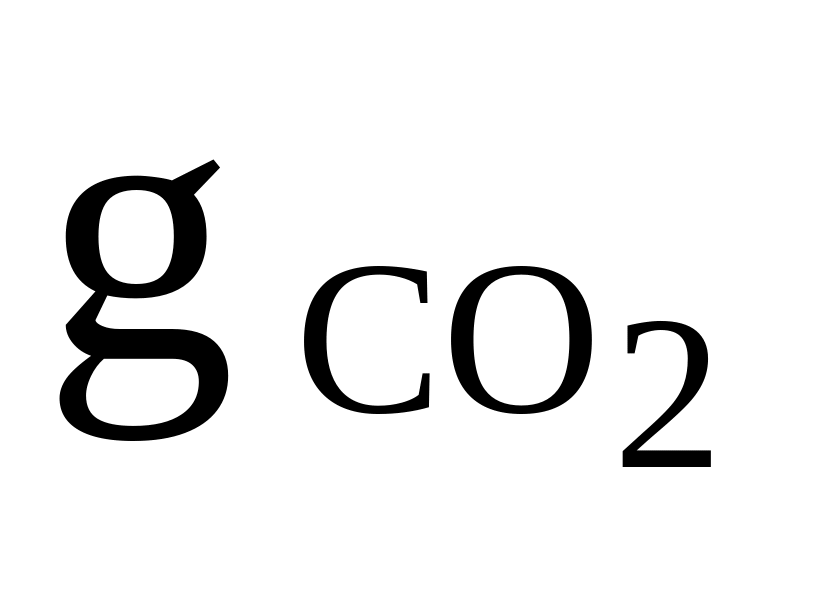= 0,3	Rсм = 250 Дж/(кгК)
11	CO2, C2H4, CO	= 0,45	cр,см = 950 Дж/(кгК)

Продолжение таблицы 1.1

1	2	3	4
12	O2, CH4, C2H6	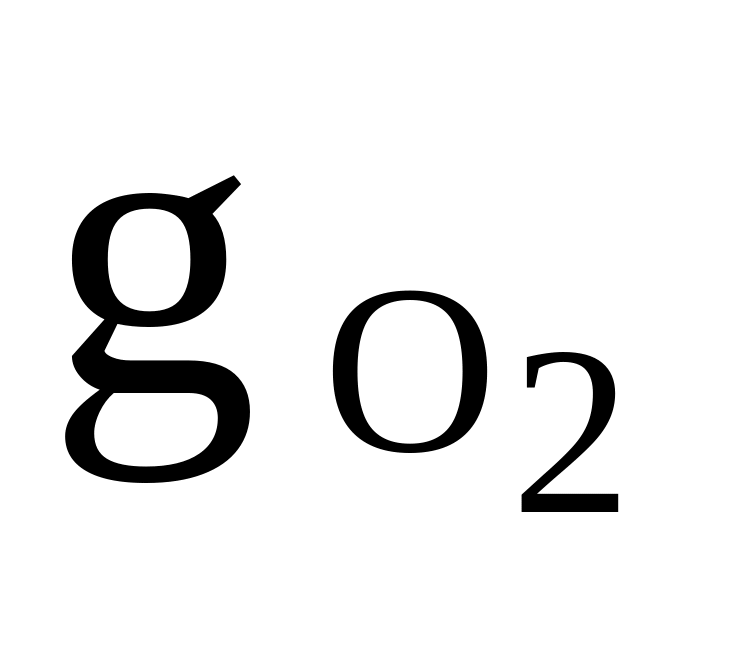= 0,4	cv,см = 1000 Дж/(кгК)
13	O2, C2H2, CH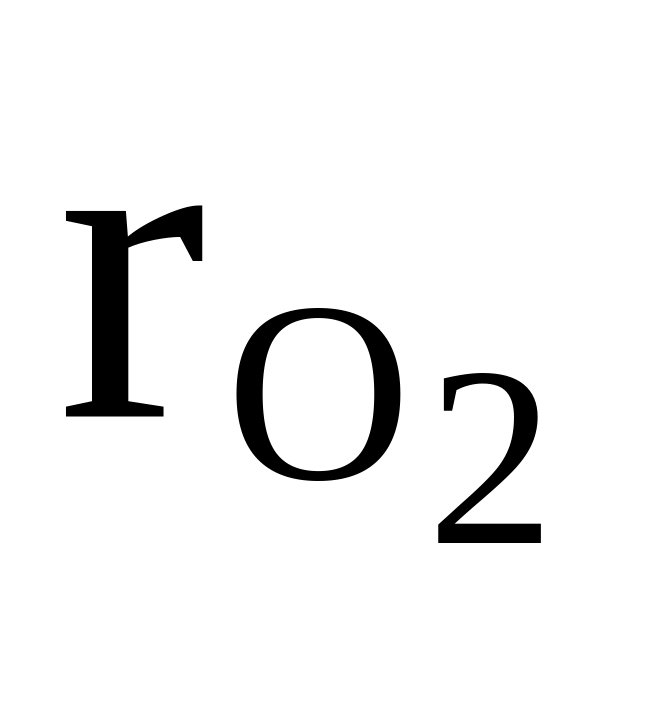4	= 0,4	см = 25 кг/кмоль
14	He, C2H6, CO	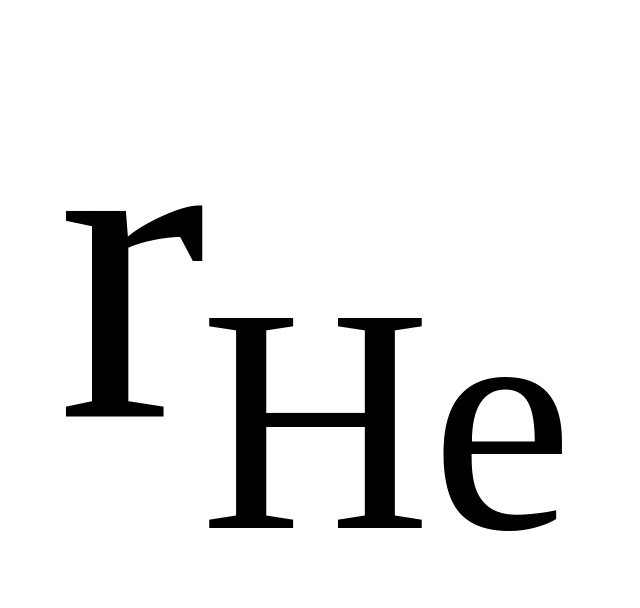= 0,6	cр,см = 25000 Дж/(кмольК)
15	CH4, Ne, NH3	= 0,35	cv,см = 20000 Дж/(кмольК)
16	N2, CO2, O2	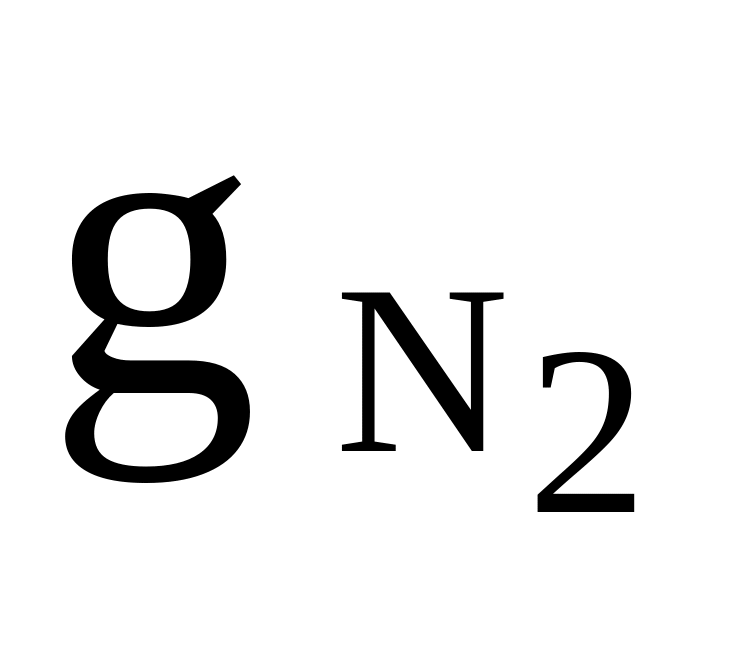= 0,4	Rсм = 260 Дж/(кгК)
17	O2, CO, CO2	= 0,2	cр,см = 900 Дж/(кгК)
18	C2H4, O2, CH4	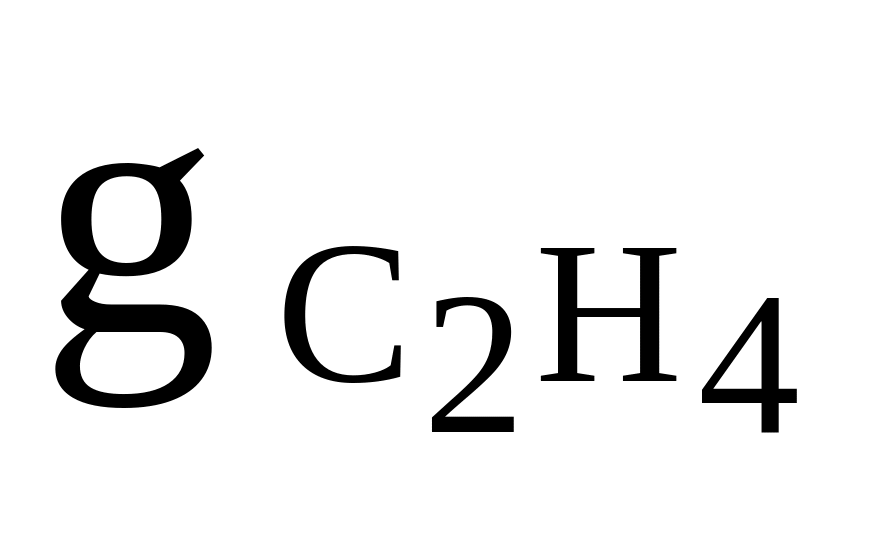= 0,3	cv,см = 950 Дж/(кгК)
19	NH3, O2, CO	= 0,5	см = 23 кг/кмоль
20	CH4, He, C2H6	= 0,55	cр,см = 29000 Дж/(кмольК)
21	CO, CH4, Ne	= 0,5	cv,см = 19000 Дж/(кмольК)
22	C2H2, N2, CO2	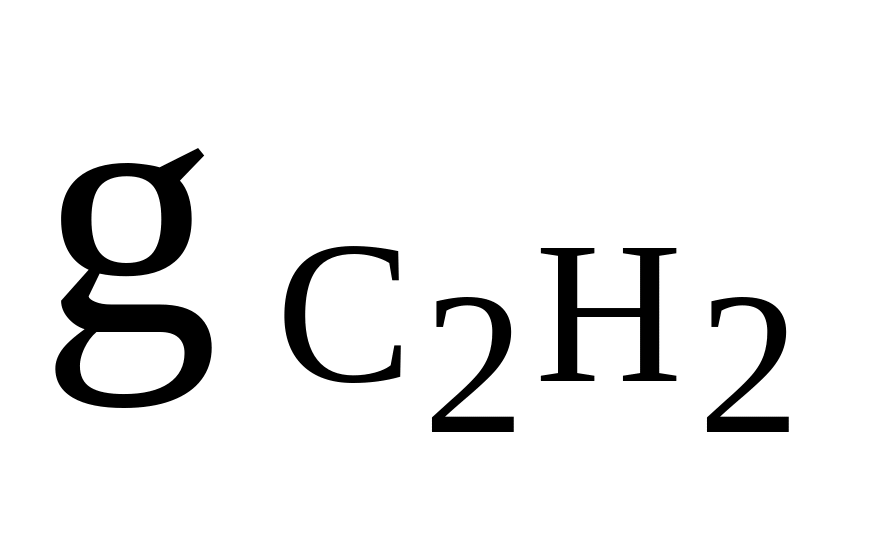= 0,25	Rсм = 255 Дж/(кгК)
23	CH4, O2, C2H4	= 0,3	cр,см = 1350 Дж/(кгК)
24	Ar, C2H4, O2	= 0,25	cv,см = 680 Дж/(кгК)
25	SO2, CO2, He	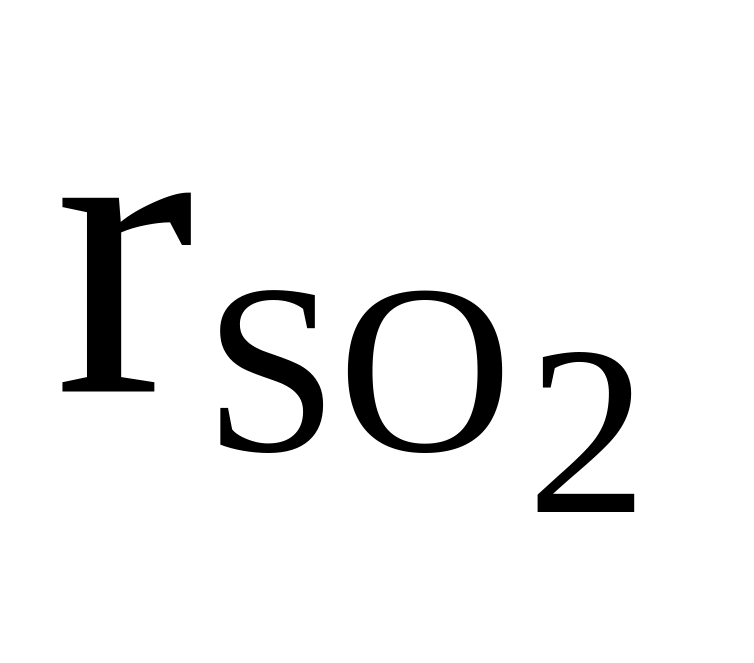= 0,2	см = 21 кг/кмоль
26	Ar, SO2, CO	= 0,14	cр,см = 29200 Дж/(кмольК)
27	CO2, CO, CH4	= 0,4	cv,см = 24000 Дж/(кмольК)
28	Ar, C2H2, N2	= 0,45	Rсм = 265 Дж/(кгК)
29	N2, He, CH4	= 0,72	cр,см = 1750 Дж/(кгК)
30	SO2, Ar, C2H4	= 0,27	cv,см = 650 Дж/(кгК)

Молекулярные массы компонентов смеси приведены в приложении табл. 1.

Таблица 1

Характеристики газов

Химическая формула газа	Молекулярная масса , кг/кмоль		Атомный вес элементов газа
Азот N2	28,01		Водород Н — 1,008
Кислород О2	32,00		Кислород О — 16,00
Окись углерода СО	28,01		Азот N — 14,007
Углекислый газ СО2	44,01		Углерод С — 12,01
Метан СН4	16,04		Сера S — 32,06
Аммиак NH3	17,03
Диоксид серы SO2	48,06
Ацетилен С2Н2	26,04
Этилен С2Н4	28,05
Этан С2Н6	30,07

Массы киломоля газов

Название газа	Химическая формула газа	Масса киломоля , кг/кмоль
Неон	Ne	20,18
Гелий	He	4,00
Аргон	Ar	39,94
Азот	N2	28,01
Кислород	О2	32,00
Окись углерода	СО	28,01
Углекислый газ	СО2	44,01
Метан	СН4	16,04
Аммиак	NH3	17,03
Диоксид серы	SO2	64,06
Ацетилен	С2Н2	26,04
Этилен	С2Н4	28,05
Этан	С2Н6	30,07

Объем задания:

1. Определить для газовой смеси:

а) массовые и объемные доли смеси;

б) молекулярную массу смеси;

в) газовую постоянную смеси;

г) массовую изохорную и изобарную теплоемкости смеси;

д) мольную изохорную и изобарную теплоемкости смеси;

е) коэффициент Пуассона смеси.

Результаты расчетов свести в табл. 1.3.

Таблица 1.3

Результаты расчета смеси идеальных газов

g1

g2

g3

r1

r2

r3

mсм,

Rсм,

mсv см,

mср см,

сv см,

ср см,

Ксм

Теоретические основы для задачи № 1

Основные уравнения и законы идеальных газов и газовых смесей

Совмещенное уравнение 1-го и 2-го законов термодинамики для обратимых процессов имеет вид:

,

,

где dl = Pdv – работа изменения объема в обратимом процессе.

Уравнение состояния идеальных газов может быть записано в виде:

— для 1 кг газа;

— для m кг газа;

— для 1 кмоля газа,

где Р – абсолютное давление, Па;

v – удельный объем газа, м³/кг;

V – объем данной массы газа, м³;

V_m – объем кмоля газа, м³/кмоль;

Т – абсолютная температура, К;

m – масса газа, кг;

m – молекулярная масса газа, кг/кмоль;

R_m = 8314 Дж/(кмоль×К) – универсальная газовая постоянная;

– газовая постоянная, Дж/(кг×К).

Согласно молекулярно–кинетической теории идеальных газов их удельные мольные и массовые изохорные и изобарные теплоемкости постоянны и рассчитываются по формулам:

, кДж/(кмольК);

, кДж/(кмольК);

;

,

где i – число степеней свободы данного газа.

Для одноатомных газов i = 3; для двухатомных газов i = 5; для трех и многоатомных газов i =6. Для смеси идеальных газов i не имеет смысла и данные формулы использовать нельзя.

Разность изобарной и изохорной теплоемкостей идеальных газов определяется соотношением Майера:

; .

В расчетах политропных процессов используется коэффициент Пуассона, который для однородного газа определяется соотношением

.

Смесь идеальных газов

Состав смеси идеальных газов может быть задан массовыми или объемными долями:

g_i = m_i / m_см – массовая доля смеси,

r_i = V_i / V_см = Р_i / P_см – объемная доля смеси,

где m_i, m_см – массы данного компонента и смеси газа,

V_i, Р_i – парциальный объем и давление данного компонента смеси газа,

V_см, Р_см – объем и давление смеси газа.

Сумма массовых и объемных долей смеси газов равна единице.

, .

Между массовыми и объемными долями газовой смеси справедливо соотношение:

или ,

где m_см – молекулярная масса смеси, которая может рассчитываться как

;

R_см – газовая постоянная смеси, она может рассчитываться как

,

причем R_см = 8314/m_см , Дж/(кмоль×К).

Массовая и мольная теплоемкости смеси идеальных газов рассчитываются как суммы алгебраических произведений массовых или объемных долей на соответствующие массовые и мольные теплоемкости компонентов смеси газов

и или .

Коэффициент Пуассона для смеси идеальных газов рассчитывается как

.

Таблица 1.2

Исходные данные для расчета политропных процессов

смеси идеальных газов

№	Р1, МПа	v1, м3/кг	t1, оС	Р2, МПа	v2, м3/кг	t2, оС	q, кДж/кг	l, кДж/кг	n
1	2	3	4	5	6	7	8	9	10
1	0,2		30	0,4					
2		0,6	120					– 100	1,5
3	0,2		100			500			0
4	0,4	0,7		0,3		20
5	0,34	0,68						70	k
6		0,8	400		0,3				1
7	1,6	0,13		0,72	3v1
8	0,55		25					200	0
9		0,35	800			600			1,15
10	0,2		20			300			
11	0,34	0,6		0,6			0
12		1,2	300		0,25v1				1,7
13	0,6		800				– 180		0
14	0,25	0,8					– 300		1,15
15		0,55	800			500	0
16	0,1		20	0,8					1
17	0,3	0,75		0,9					1,2
18		0,44	780					– 140	0
19	1		300		3v1				1,6
20	0,32	0,65					100		
21		0,1	200	0,2					1
22	0,25		25	2		125
23	1	0,2				900			0
24		0,6	250				90		0,35
25	0,12		20		0,4				k
26	0,4	0,5				950			
27		0,32	100	2		175
28	2		900		0,1				0
29	1,3	0,16						50	0,4
30		0,1	17		0,5				1

Объем задания:

2. Расчет процесса изменения состояния смеси идеальных газов.

В результате этого расчета необходимо определить:

а) начальные и конечные термические параметры процесса Р, v, t;

б) количество теплоты, работу изменения объема, изменение внутренней энергии, энтальпии и энтропии. Эти величины определяются для 1 кг смеси газа.

Результаты расчетов свести в табл. 1.4, 1.5.

3. Построить процесс в диаграммах Р,v и Т,s в масштабе.

Результаты расчетов свести в табл. 1.4, 1.5.

Таблица 1.4

Результаты расчета параметров состояния

политропного процесса 1-2 смеси идеальных газов

Р1	t1, oC	v1, м3/кг	Р2	t2, oC	v2, м3/кг

Таблица 1.5

Таблица 1.5

Результаты расчета энергетических характеристик политропного процесса 1-2 смеси идеальных газов

Процесс (название)	n	q, кДж/кг	l, кДж/кг	Du, кДж/кг	Dh, кДж/кг	Ds, кДж/(кг×К)

Политропные процессы изменения состояния идеальных газов

Расчет и анализ политропных процессов идеальных газов проводится на основании уравнений и законов термодинамики. В табл. 1.6 приведены основные расчетные формулы для определения основных параметров состояния (Р, v, Т), мер энергетического взаимодействия (q, l), изменения энергетических параметров (Du, Dh, Ds), значения теплоемкости, показателя политропы n, коэффициента a, определяющего закономерность преобразования форм энергии: a = Du/q, как для произвольного политропного процесса, так и для частных (основных) процессов идеальных газов: изобарного (Р= const), изохорного (v = const), изотермического (T = const), адиабатного — изоэнтропного (dq = 0 или s = const).

Если для политропного процесса показатель политропы не задан в явном виде, то он может быть определен по одному из уравнений, связывающих три основных параметра или по известному коэффициенту a, теплоемкости процесса, работе изменения объема, теплоте процесса и т.п.

На рис. 1.1 и 1.2 в диаграммах Р,v и T,s изображены основные термодинамические процессы идеальных газов, указаны значения их показателей политропы и показаны границы изменения показателя политропы для всех возможных областей прохождения политропных процессов.

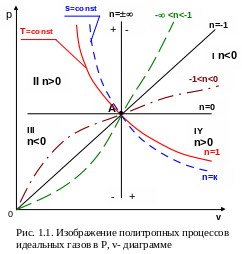
Таблица 1.6

Основные расчетные выражения для политропных процессов идеальных газов

Процессы	n	с	a	Уравнение	q	l	Ds	Du, Dh
Р = const	0	сp	1/К		сp Dt	Р Dv = R DТ
v = const	±¥	cv	1		cv Dt	0
T = const	1	±¥	0
s = const (dq = 0)	К	0	±¥		0	u1 – u2 = =cv(T1 – T2) = =	0	Du = cv(t2-t1), Dh = cp(t2-t1)
политропа n = const (a = const)					с Dt	= =