Лекція № 6 «Ламінарний режим руху рідини у трубах»

1. Загальні відомості про визначення втрат напору в трубопроводі.

2. Закон розподілу швидкостей по перетину круглої труби при ламінарному режиму течії рідини.

3. Видаток і середня швидкість ламінарного потоку.

4. Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.

5. Початкова ділянка ламінарної течії.

1. Загальні відомості про визначення втрат напору в трубопроводі.

Втрати напору на тертя вздовж потоку рідини, які виникають при рівномірному напорному русі рідини в трубах, визначають за формулою Дарсі-Вейсбаха, яка є універсальною:

, м (1)

де l – довжина ділянки трубопроводу, м;

d – внутрішний діаметр трубопроводу, м;

V – середня швидкість потоку, м/с;

g – прискорення вільного падіння, м/с²;

– безрозмірний коефіцієнт гідравлічного тертя.

Теорія гідродинамічної подібності говорить про те, що  повинен бути функцією числа Re , а також може залежати від безрозмірного геометричного фактору , де  - шорсткість стінок трубопроводу.

Абсолютною шорсткістю  називають висоту нерівностей – виступів на внутрішніх поверхнях трубопроводу.

При турбулентному режимі, на відміну від ламінарного, шорсткість стінок істотно впливає на опір руху рідини, тому що сприяє турбулізації потоку.

Втрати тиску на тертя по довжині трубопроводу визначають за формулою:

, Па, (2)

де ρ – густина рідини, кг/м³.

Місцеві втрати напору| викликаються|спричиняють| опорами в арматурі, фасонних частинах|частках| і устаткуванні|обладнанні|, внаслідок|внаслідок| звуження і розширення потоку, зміни напряму|направлення| руху рідині, злиття і розділення|поділу| потоку тощо.|тощо|

Втрати на подолання|здолання| місцевих опорів в зовнішніх мережах|сітях| водопроводу зазвичай|звично| не перевищують 10-15%, у внутрішніх мережах|сітях| – 30% від втрат напору| по довжині.

Проте|однак| місцеві втрати напору| в деяких видах інженерних мереж|сітей| можуть досягати значної величини: так, наприклад, в системах опалювання будівель – до 40%, у повітроводах| вентиляційних систем і пневмотранспорті| – до 60-70% від втрат напору| по довжині.

Місцеві втрати напору визначають як швидкісний напор безпосередньо поблизу місцевого опору по формулі Вейсбаха:

. (3)

Загальної теорії для визначення коефіцієнтів місцевих опорів, за виключенням окремих випадків, немає. Тому коефіцієнти місцевих опорів, визначають дослідним шляхом. Значення їх для різних елементів трубопроводів наводяться в технічних довідниках.

2. Закон розподілу швидкостей по перетину круглої труби при ламінарному режиму течії рідини.

Ламінарний рух рідини зустрічається досить рідко. У трубах ламінарний рух здійснюється в умовах перекачування в’язких мастил, мазуту та їм подібних рідин особливо при низьких температурах і невеликих швидкостях перекачування.

Ламінарна течія у круглій циліндричній трубі відбувається без поперечних переміщень частинок рідини, тобто паралельними шарами. В даному випадку можна уявити, що ці шари скручені у концентричні трубки, які рухаються поступально вздовж вісі труби, ковзаючи одна відносно другої, причому кожна така трубка повністю зберігає свою форму.

Вміння розраховувати видаток у ламінарному режимі, визначити втрати енергії, знати закон розподілу швидкостей і вміти виконати потрібні розрахунки – ось ті питання, які являють практичний інтерес для інженера-механіка.

Ламінарна течія внаслідок своєї простоти піддається теоретичному аналізу.

Теорія ламінарної течії рідини ґрунтується на законі тертя І. Ньютона. Це тертя між шарами рухомої рідини є джерелом втрат енергії у даному випадку.

Розглянемо сталу ламінарну течію рідини у круглій трубі (рис. 1) радіусом r. Щоб виключити вплив сили тяжіння і цим спростити вивід, припустимо, що труба розташована горизонтально. Виділимо в цьому потоці достатньо далеко від входу до неї, де потік вже стабілізувався, відрізок довжиною l між перетинами 1-1 і 2-2. Нехай у перетині 1-1 тиск буде дорівнювати p₁, а в перетині 2-2 – p₂ . З огляду постійності діаметру труби, швидкість рідини буде постійною, а коефіцієнт  буде незмінним вздовж потоку внаслідок його стабільності.

В цих умовах рівняння Д. Бернуллі для вибраних перетинів прийме вигляд:

.

Звідси , що і показують п’єзометри, які встановлені у вибраних перетинах.

Цей результат показує, що при рівномірній течії зменшення статичного напору дорівнює питомій енергії, яка витрачена на переборення сил тертя.

Виділимо у цьому потоці циліндричний об’єм рідини радіусом h і довжиною l. При русі цього циліндру на його боковій поверхні виникає сила внутрішнього тертя Т. Запишемо рівняння рівноваги рівномірного руху виділеного об’єму рідини у трубі відносно вісі потоку, враховуючи, що на об’єм рідини діє сила, яка викликає рух і сила опору.

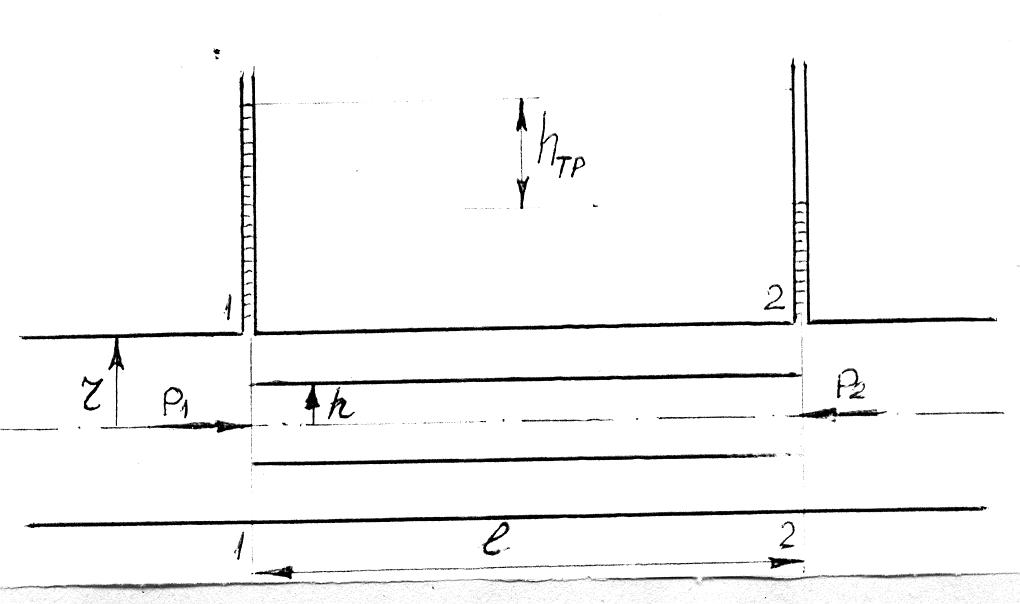
Рис.1 Схема установки для дослідження ламінарного режиму

Рухомими силами у даному випадку є сили тиску, рівнодіюча яких визначається:

Р=(р₁ – р₂)  h²

Рівняння рівноваги:

Р=Т

Визначимо силу внутрішнього тертя Т:

T = – ^. F ,

де  - динамічний коефіцієнт в’язкості,  = ;

F – бокова поверхня стискаємих шарів, F = 2hl.

Знак “–“ прийнято тому, що від’ємний (з ростом відстані від вісі потоку h швидкість частин рідини U зменшується).

Підставимо у загальне рівняння рівноваги значення сил:

,

або:

Поділимо останній вираз на gl, після чого одержимо:

,

або:

Якщо врахувати, що є J – гідравлічний уклон, то

Градієнт швидкості з попереднього рівняння буде:

Розділимо змінні і отримаємо:

.

Після інтегрування:

Постійну інтегрування С знайдемо з граничної умови: при h=r, U=0 (внаслідок прилипання рідини до стінок).

,

звідси:

Підставляючи значення постійної С, одержимо:

Таким чином, ми прийшли до висновку, що швидкість частин рідини пропорційна квадрату відстані її від вісі труби.

Цей вираз дає значення швидкості на будь-якій відстані h від вісі труби і відомий як закон Дж. Стокса.

Аналізуючи одержаний вираз, приходимо до висновку, що при ламінарному русі рідини ми маємо параболічний розподіл швидкостей.

Внаслідок цього епюра швидкостей при ламінарному русі (рис. 2) буде мати форму параболи.

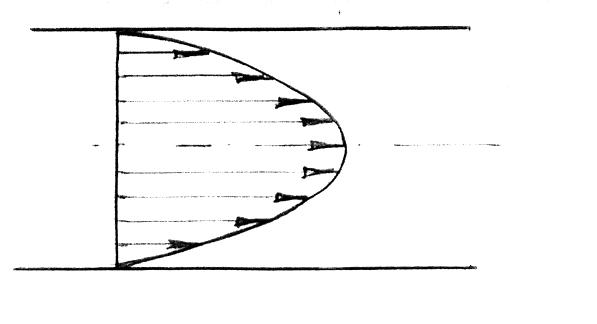
Рис. 2 Епюра швидкостей при ламінарному режиму руху рідини

При h=0,

Як відомо, величина дотичної напруги у потоці рідини визначається виразом:

В той же час і тоді:

Із останнього виразу видно, що при ламінарному режимі руху рідини зміна  вздовж радіусу відбувається по лінійному закону, причому буде при h=r, тобто біля стінки труби, а _min=0, буде при h=0, тобто на вісі труби.