2. Сили тиску рідини на плоскі поверхні.

Визначення сили тиску рідини, що діє на ту або іншу поверхню, має велике практичне значення при механічних розрахунках стінок, заглушок, перегородок, мембран та інших пристроїв.

Доведення питання про силу тиску рідини на плоску стінку зручніше проводити в координатних осях, одна з яких спрямована уздовж стінки.

Почнемо з більш загального випадку – визначення сили тиску рідини на плоску поверхню (рис. 6), яка нахилена до обрію під кутом α, і яка має площу F.

Нехай вільна поверхня знаходиться під впливом надлишкового тиску р_м, який може бути виражений відповідною п’єзометричною висотою . Тому становить інтерес тільки сила надлишкового тиску.

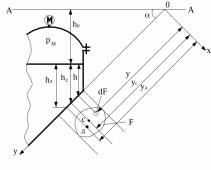
Рис. 6 Визначення сили тиску рідини на плоску поверхню.

За ось координат у приймемо лінію, яка збігається з напрямком плоскої стінки, і продовжимо цю лінію до перетинання з п’єзометричною площиною A-A у точці О. З точки О проведемо ось Ox, яка є нормальною до поверхні стінки. Для зручності розгляду стінку повернемо навколо осі Oy до з’єднання з площиною креслення. Тоді на площині побачимо фігуру в натуральну величину. Визначимо величину сили тиску рідини на стінку. Відзначимо, що на різні точки площі F, що знаходяться на різних глибинах, діють відповідно до основного рівняння гідростатики різні тиски. Знайдемо силу тиску на елементарну площадку. При цьому відстань елементарної площадки dF від осі Ox буде дорівнювати y. Надлишковий гідростатичний тиск в області площадки dF може бути прийнятий рівним . Тоді елементарна сила dР визначиться:

,

де – відстань по вертикалі від даної точки до п’єзометричної площини A-A. З рис. 6 видно, що . Отже, елементарна сила тиску буде:

.

Повна сила тиску на всю площу F визначається сумою елементарних сил:

.

Вираз являє собою статистичний момент площі відносно осі x. Він дорівнює площі фігури F, яка помножена на координату центра тяжіння у_с цієї площі. Тому:

,

де:

або: ;

але:

і тоді: ;

Отже, сила сумарного тиску, що діє на плоску фігуру, яка занурена в рідину, виражається добутком площі фігури на величину гідростатичного тиску в центрі її тяжіння.

Якщо р_м = 0, то сила надлишкового тиску дорівнює Р = F ∙ ρg ∙h_c. Добуток F ∙ h_c являє собою об’єм циліндра з площею основи F і висотою h_c. З урахуванням цього, формулу Р = F ∙ ρg ∙h_c можна прочитати так: сила, з якою рідина діє на плоску стінку, дорівнює вазі рідини в об’ємі циліндра з основою, рівною площі даної стінки, і висотою, рівній глибині занурення центра тяжіння цієї площі під рівень вільної поверхні.

Формулу Р = F ∙ ρg ∙h_c можна спростити. Так як ρg ∙h_c є гідростатичний тиск у центрі тяжіння площі F, то справедлива рівність:

Р_с = ρg ∙h_c ,

тобто подібно тому, як гідростатичний тиск не залежить від розмірів резервуара, у якому знаходиться нерухома рідина, так і сила тиску P рідини на плоску стінку, яка визначається з формул:

Р = р_оF + F∙ ρg ∙h_c і Р = F ∙ ρg ∙h_c

також не залежить ні від об’єму рідини в резервуарі, ні від розмірів бокових стінок резервуара, а тільки від величини даної площадки, на яку діє рідина, і від глибини занурення її центра тяжіння під рівень вільної поверхні. Крім того, з отриманого виразу видно, що сила тиску на плоску стінку не залежить від кута нахилу цієї стінки.

Як було показано раніше, горизонтальна площина в нерухомій рідині є поверхнею рівного тиску. Будь-яка точка на такій площині зазнає однаковий тиск Р = р_о + ρg ∙h_c. Отже, сила повного гідростатичного тиску рідини на горизонтальну площадку F визначиться як: (2).

Р = рсF = F ( ро + ρg ∙hc)

Припустимо, що ми маємо три судини з плоскими днищами (рис. 7). При цьому форма судин різна, але площа дна F і глибина води H у всіх судинах однакова. За таких умов кількість рідини в трьох судинах буде різна.

Рис. 7 Гідростатичний парадокс.

На перший погляд здається, що сила тиску рідини на дно буде різна, оскільки різна кількість рідини і, отже, різна сила її тяжіння.

Визначимо силу тиску рідини, яка діє на дно судин:

Р_А = F∙ ρg ∙H; Р_Б = F∙ ρg ∙H; Р_В = F∙ ρg ∙H.

Таким чином, посудини різної форми, але з однаковою площею дна і наповнених рідиною на однакову висоту, мають однакову силу тиску на дно. Це положення в гідравліці зветься «гідростатичним парадоксом».

Розглянемо, звідки береться в судині Б додаткова сила в порівнянні із судиною А и куди подінеться надлишок ваги рідини в судині В у порівнянні із судиною А. Чи нема тут протиріччя з законами фізики?

Закони гідравліки стверджують, що сила тиску рідини не залежить від форми судин, а залежить від глибини занурення і її розмірів. На поставлене питання дають пояснення особливі властивості рідини - передавати зовнішній тиск в усіх напрямках і з однаковою силою (закон Паскаля).

Наприклад, на дно судини В діє сила сумарного гідростатичного тиску Р=_сF=gНF. Що стосується рідини в об’ємах abc і а'b'с', то її вага сприймається стінками, а не дном судини. Безумовно, якщо судина буде стояти на столі, то стіл буде сприймати вагу всієї рідини, що знаходиться в судині.

Отже, сила тяжіння рідини, якою наповнена судина, може відрізнятися від сили тиску, що діє на дно судини і ніякого протиріччя між законами фізики і гідравліки не існує.

Великий інтерес представляє знаходження центра тиску (рис. 6). Точка Д прикладання рівнодіючої сил тиску називається центром тиску. Відповідно до основного рівняння гідростатики тиск, який діє на поверхні рідини, рівномірно розподіляється по площі фігури, а тому точка прикладення сумарної сили поверхневого тиску Р = р_оF буде співпадати з центром тяжіння фігури. Навпаки, сумарна сила надлишкового гідростатичного тиску, який розподілений по площі фігури нерівномірно, буде знаходитись нижче центра тяжіння. Якщо на фігуру з усіх боків діє атмосферний тиск (найбільш частий випадок із практики), прикладання центра тиску залежить не від величини сили поверхневого тиску, а тільки від величини сили надлишкового тиску, який діє на фігуру. У тому ж випадку, коли поверхнева сила відмінна від атмосферного тиску і діє тільки з однієї сторони фігури, точка прикладання сили сумарного абсолютного гідростатичного тиску буде лежати нижче центра тяжіння фігури і залежати не від положення центра надлишкового тиску. Отже, визначимо координату точки Д прикладання центра тиску.

З механіки відомо (теорема Варіньйона), що момент рівнодіючої системи рівнобіжних сил дорівнює сумі моментів сил, які її складають. У нашому випадку рівнодіючою є сила сумарного надлишкового тиску:

Р_н = F∙ ρg ∙h_c = F∙ ρg ∙ у_с ∙ sin α,

а складовими силами, з яких складається сила Р_н – сили елементарного надлишкового тиску dР_н = ρg ∙h∙ dF, які діють на елементарно малі площадки dF.

Складемо вираз для елементарного моменту нескінченно малої сили dР_н відносно осі Ox, з урахуванням що h = у ∙ sin α:

dM = dР_н ∙ y = dF ρg ∙h∙ y = dF ρg ∙h∙ y²∙ sin α.

Визначимо суму всіх елементарних моментів М_с. Вона буде виражатися інтегралом по площі F:

але - це момент інерції фігури, яка розглядається відносно осі Ox, тобто , а тому М_с = ρg ∙ sin α ∙ І_х.

Момент рівнодіючої сили Р_н може бути записаний:

M_р = Р_н ∙ y_д = F∙ ρg ∙h_с∙ y_д,

де у_д – відстань точки прикладання рівнодіючої Р_н від осі Ox, що є координатою центра тиску, який ми визначаємо. Так як М_с = M_р, то ρg ∙ sin α ∙ І_х = F ∙ ρg ∙у_с ∙ sin α ∙ y_д або, І_х = F ∙у_с∙ y_д звідки:

Замінимо момент інерції І_х через центральний момент інерції І₀, тобто через момент інерції фігури відносно осі, яка проходить через її центр тяжіння. Ці два моменти пов'язані залежністю:

,

тоді: . (3)

Отже, центр надлишкового гідростатичного тиску лежить нижче центра тяжіння фігури на величину . Позначимо відношення через е, тоді: y_д = у_с + е , (4)

де е має розмірність довжини (метри стовпа рідини) та іноді називається ексцентриситетом.

Слід до цього додати, що для полегшення обчислень у_с та y_д геометричних фігур, які найбільш часто зустрічаються, в літературних джерелах наведені спеціальні довідкові таблиці.

Отже, сила, з якою рідина діє на плоску стінку, дорівнює вазі рідини в об’ємі циліндра з основою F (площа даної стінки), і висотою h_с (глибина занурення центра тяжіння під рівень вільної поверхні).

На підставі отриманого висновку можна стверджувати, що в графічному зображенні сила Р представлена як вага циліндричного об’єму, який має назву тіла тиску. Отже, при графічному способі визначення сили тиску рідини на поверхню вона буде дорівнювати:

Р = F_еп∙ b,

де F_еп - площа епюри тиску, м²;

b - ширина плоскої стінки, м.

Центр тиску визначається як проекція центра тяжіння тіла тиску на площину даної стінки.

Очевидно, що вектор сили тиску у всіх випадках проходить через центр тяжіння епюр тиску, положення якого можна визначити або аналітично (як це показано раніше), або графічно (рис. 8).

Рис. 8 Графічне визначення центру тяжіння епюри гідростатичного тиску.

Графічне рішення зводиться до наступного: на продовженні верхньої основи трапеції BCDE відкладають відрізок NE, який дорівнює нижній основі трапеції DC. Потім продовжують нижню основу в протилежному напрямку, на якому відкладають відрізок CM, який дорівнює верхній основі. Знаходять середини основ трапеції і проводять пряму tk (медіану). Кінці відрізків у точках N і M з'єднують прямою. Точка перетинання прямих tk і NM і є центром тяжіння трапеції. Провівши через точку O вектор сили P, знаходять точку прикладання цієї сили D.

Визначимо силу тиску рідини на стінки відводу (рис.9). Нехай маємо відвід ABCE, в якому тиск в перетинах AB і CE дорівнює , діаметр труби D, а кут між перетинами AB і CE дорівнює . Визначимо силу , яка розриває відвід.

Силу тиску у розглянутих перетинах AB і CE визначимо з виразу:

.

Рис. 9 Сили гідростатичного тиску, які діють на стінки відводу.

Перенесемо ці сили по лінії дії до точки їх перетинання і побудуємо у цій точці паралелограм сил. Одержимо ромб, тому що обидві сили рівні між собою. Крім того, сили перпендикулярні перетинам, на які вони діють, внаслідок чого гострий кут ромба дорівнює . Діагоналі ромба взаємно перпендикулярні і поділяються навпіл, тому можна написати:

.