106.2.3 Неупругий удар
Абсолютно упругий удар макроскопических тел – это идеализация, так как реально часть их исходной энергии при ударе непременно теряется, расходуясь на некоторое разрушение кристаллической решетки, а также на звуковые волны в окружающей среде. Считается, что абсолютно упругий удар могут испытывать только микрочастицы.
Для характеристики степени упругости удара вводится коэффициент восстановления k. Для прямого удара шаров он определяется соотношением:
(106.9)
где и - скорости тел до удара, и - скорости тел после удара. Для абсолютно упругого удара - = - , и k=1. Для абсолютно неупругого = , и k=0. Для просто неупругого 0<k<1. Значение k можно определить экспериментально, например, по высоте h, на которую подскакивает шарик, свободно падающий на горизонтальную плиту с высоты H:
(106.10)
(так как плита
неподвижна, для нее
=
= 0,
а для шарика
).
Коэффициент восстановления считается зависимым только от материала тел. Согласно опытам, при ударе шаров: из дерева - k ≈ 0,5; из мягких сталей - k ≈ 0,7; из слоновой кости - k ≈ 0,9; из стекла - k ≈ 0,94.
В данной работе коэффициент k определяется по скоростям двух одинаковых соударяющихся шаров, один из которых вначале неподвижен.
106.2.4. Сила удара. Радиус контактной площадки. Давление.
При прямом абсолютно
упругом ударе первого шара о такой же
неподвижный второй шар, первый
останавливается, теряя импульс p=mv1.
Из второго закона Ньютона следует:
,
где τ
– время взаимодействия шаров при ударе
(время удара), а
- импульс
силы. Средняя
сила взаимодействия шаров за время τ:
(106.11)
Время удара в работе измеряется при помощи баллистического гальванометра. Очевидно, что при ударе сила взаимодействии растет от нуля (при начале контакта) до максимальной (при максимальном сжатии), а затем снова падает до нуля. Зависимость F(t) имеет сложный вид (см. рис.106.3), однако с достаточной точностью можно считать, что она имеет треугольный вид, и тогда Fmax ≈ 2<F>.
Рис.106.3.
Для оценки давления
при ударе воспользуемся соотношением
где
- максимальная площадь контакта при
сжатии шаров, r
– радиус контактной площадки (рис.
106.4а).
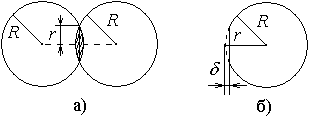
Рис.106.4
Из (рис.106.4б) видно, что
, (106.12)
считая δ << R, где R – радиус шара. Деформация δ – это расстояние, на которое смещается первый шар за первую половину удара, т.е. за время τ / 2, следовательно δ = <v1> τ / 2. Так как скорость удара за это время меняется от v1 до 0, то можно считать, что <v1> ≈ v1 / 2. Таким образом δ = v1 τ / 4, и тогда радиус контакта:
(106.13)
Тогда для давления получим:
(106.14)
106.3. Описание лабораторной установки
Установка для измерения времени удара τ и коэффициента восстановления k содержит: два стальных шарика, подвешенных к кронштейну на гибких проводах; шкалу, показывающую углы отклонения шаров; электромагнит, удерживающий первый шарик в исходном положении; электрическую схему (состоит из баллистического гальванометра, магазина сопротивлений и электрического конденсатора, подсоединенных к шарам и электромагниту), позволяющую определить время удара шаров. Принципиальная электрическая схема установки приведена на рис.106.5. Тумблер SA управляет работой электромагнита. Тумблер SA1 служит для обнуления заряда конденсатора С. Тумблер SA2 позволяет зарядить конденсатор до начального напряжения. Гальванометр G используется для определения напряжения на конденсаторе. Магазин сопротивлений используется в качестве эталонного сопротивления Rм.
Рис.106.5