
- •Механика. Гидравлика
- •Часть II
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок обработки опытных данных
- •Порядок выполнения работы
- •Порядок обработки опытных данных
- •Отогнанный гидравлический прыжок (рис.15);
- •Порядок выполнения работы
- •Порядок обработки опытных данных
- •Литература
Министерство образования и науки
Вологодский государственный технический университет
Кафедра водоснабжения и водоотведения
Механика. Гидравлика
Методические указания к выполнению лабораторных работ
Часть II
Факультеты: экологии;
инженерно – строительный
Специальности: 270112, 270205, 270102, 270105, 280302
Бакалавриат: 270100
Вологда
2010
УДК 378.147:532
Механика. Гидравлика. Методические указания к выполнению лабораторных работ. Часть II. - Вологда: ВоГТУ, 2010. – 48 с.
Методические указания предназначены для студентов очной и заочной форм обучения специальностей 270112, 270205, 270102, 270105, 280302 и бакалавриата 270100, изучающих дисциплины: «Механика. Гидравлика», «Прикладная механика жидкости и газа».
В методических указаниях сформулирована цель лабораторных работ, представлены общие положения, раскрывающие физическую сущность гидравлических явлений и процессов, показан порядок выполнения работ и обработки опытных данных
Утверждено редакционно-издательским советом ВоГТУ
Составители: Тянин А.Н., канд. техн. наук, доцент
Нешатаева А.В., канд. техн. наук, доцент
Рецензент: Лебедева Е.А., канд. техн. наук, доцент
ЛАБОРАТОРНАЯ РАБОТА № 1
ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ В ПОПЕРЕЧНОМ СЕЧЕНИИ ОТРЫТОГО ПОТОКА
Цель работы
Выяснить характер распределения скоростей в живом сечении открытого плавно изменяющегося потока.
Определить коэффициент неравномерности распределения скоростей
 (коэффициент Кориолиса) и
(коэффициент Кориолиса) и
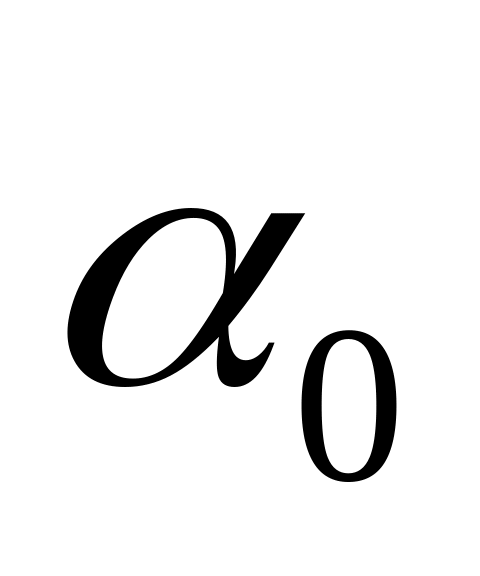 (коэффициент Буссинеска).
(коэффициент Буссинеска).
Построить эпюры скоростей в живом сечении потока.
Общие сведения
Скорости u
(действительные или осредненные)
движения отдельных частиц вязкой
жидкости различны по величине в отдельных
точках поперечного сечения потока.
Разбивая живое сечение потока на
элементарные площадки
![]() ,
можно расход потока жидкости записать
как сумму элементарных расходов
,
можно расход потока жидкости записать
как сумму элементарных расходов
![]() .
.
Частицы жидкости в различных точках сечения обладают различной кинетической энергией, которую можно найти из выражения:
![]() ,
,
где
![]() - масса элементарного объема жидкости
- масса элементарного объема жидкости
![]() ,
проходящей
за время
,
проходящей
за время
![]() через живое сечение
:
через живое сечение
:
![]()
![]()
где
![]() - элементарный расход через площадку
при скорости
- элементарный расход через площадку
при скорости
![]() движения отдельных частиц вязкой
жидкости:
движения отдельных частиц вязкой
жидкости:
![]()
![]()
Кинетическая энергия жидкости, протекающей через элементарное сечение за единицу времени (1 секунда) равна:
![]()
Кинетическая
энергия жидкости, протекающей через
все живое сечение
![]() за единицу времени равна:
за единицу времени равна:
![]() (1)
(1)
Величина кинетической
энергии
![]() той же массы жидкости в предположении,
что скорости
во всех точках рассматриваемого живого
сечения одинаковы и равны средней
скорости
той же массы жидкости в предположении,
что скорости
во всех точках рассматриваемого живого
сечения одинаковы и равны средней
скорости
![]() ,
равна:
,
равна:
![]() (2)
(2)
Значение кинетической энергии, вычисленное по выражению (2) всегда меньше, чем действительное, вычисленное по выражению (1) с учетом местных скоростей.
Отношение
действительной кинетической энергии
потока
![]() к кинетической энергии, вычисленной по
средней скорости
,
обозначают через
и называют коэффициентом Кориолиса.
Коэффициент
можно представить в виде:
к кинетической энергии, вычисленной по
средней скорости
,
обозначают через
и называют коэффициентом Кориолиса.
Коэффициент
можно представить в виде:
 (3)
(3)
Числовое значение коэффициента всегда больше единицы, причем, чем больше неравномерность распределения скоростей по живому сечению, тем больше величина .
Для равномерного
турбулентного напорного потока в трубе
с круглой формой поперечного сечения
коэффициент
![]() .
Для равномерного ламинарного движения
жидкости в тех же условиях
.
Для равномерного ламинарного движения
жидкости в тех же условиях
![]() .
.
Действительное
количество движения массы жидкости
![]() ,
протекающей через живое сечение
за одну секунду,
определяется из выражения:
,
протекающей через живое сечение
за одну секунду,
определяется из выражения:
![]()
Количество движения жидкости, протекающей через живое сечение , в каждой точке которого скорости различны (действительное количество движения при неравномерном распределении скоростей по сечению), будет равно:
![]() (4)
(4)
Количество движения той же массы жидкости, подсчитанное в предположении, что скорости во всех точках плоского живого сечения одинаковы и равны средней скорости равно:
![]() (5)
(5)
Отношение действительного количества движения массы жидкости, протекающей через плоское живое сечение потока за единицу времени (1 секунду), к количеству движения, которое имела бы та же масса жидкости, если бы все частицы жидкости обладали одинаковыми в данном сечении скоростями, равными средней скорости течения , называется коррективом количества движения или коэффициентом Буссинеска. Коэффициент Буссинеска можно представить в виде:
 (6)
(6)
Числовые значения
коэффициента
всегда
больше единицы. Чем больше неравномерность
скоростей в живом сечении, тем больше
величина коэффициента
.
При равномерном турбулентном напорном
потоке в трубопроводе с круглой формой
поперечного сечения
![]() .
Для равномерного ламинарного движения
в тех же условиях
.
Для равномерного ламинарного движения
в тех же условиях
![]() .
.
При выполнении данной лабораторной работы опыты проводят в гидравлическом лотке (рис.1), который имеет прямоугольную форму поперечного сечения.
Для регулирования глубины воды и скорости течения используют жалюзный затвор 1, установленный в конце лотка. Расход, проходящий по лотку, изменяют с помощью задвижки 2, установленной на трубопроводе перед стационарным мерным водосливом. Отметки горизонта воды в гидравлическом лотке измеряют шпитценмасштабом 4.
Для измерения скорости движения частиц жидкости используют микровертушку 3. Микровертушка крепится на измерительной игле и может быть расположена в любой точке поперечного сечения потока жидкости.
