2.4.3. Перевірка адекватності отриманої рмфм за критерієм Фішера.

Перевірку адекватності отриманої РМФМ можна проводити тільки за умови N – NK > 0, тобто, коли в РМФМ відсутній хоча б один член.

N - число досвідів у матриці;

NK – число коефіцієнтів регресії в поліномі, що являє собою математичну модель для досліджуваного процесу.

Робімо перевірку адекватності отриманої РМФМ, використовуючи критерій Фішера, розрахункове значення якого FR порівнюємо з табличним FT. Якщо FR < FR, то гіпотеза про адекватність отриманої РМФМ не відкидається.

Розрахункове значення критерія Фішера:

= = якщо >

= = якщо >

- дисперсія середнього значення вихідного параметра;

- дисперсія, що характеризує помилку досвіду (дисперсія відтворюваності);

- дисперсія, що характеризує неадекватність;

- дисперсія, що характеризує розсіювання середніх експериментальних значень .

Корістуючись формулою отриманої шуканої РМФМ процесу й таблицею №2, знаходимо YRU.

Розрахунок зведений у таблицю №3.

Табліця 2.3

U	YRU		- YRU	( - YRU)­
1.	100,5	100	- 0,5	0,25
2.	94,5	95	0,5	0,25
3.	89,5	90	0,5	0,25
4.	87,5	87	-0,5	0,25
5.	125,5	125	-0,5	0,25
6.	119,5	120	0,5	0,25
7.	114,5	115	0,5	0,25
8.	104,5	104	-0,5	0,25
			0	2

=

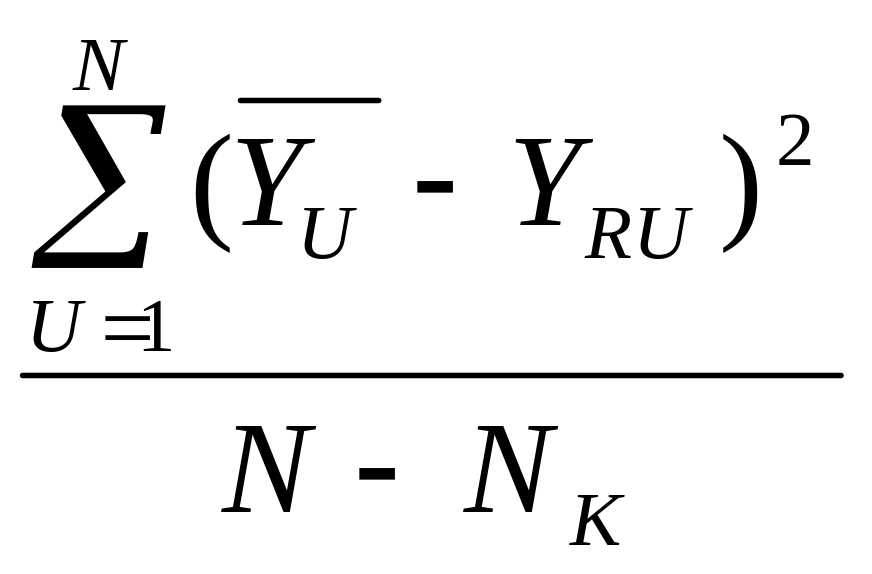
Так як більше, ніж то для визначення розрахункового значення критерію Фішера використаємо формулу:

,

А у випадку, коли менше ніж використовуємо формулу:

;

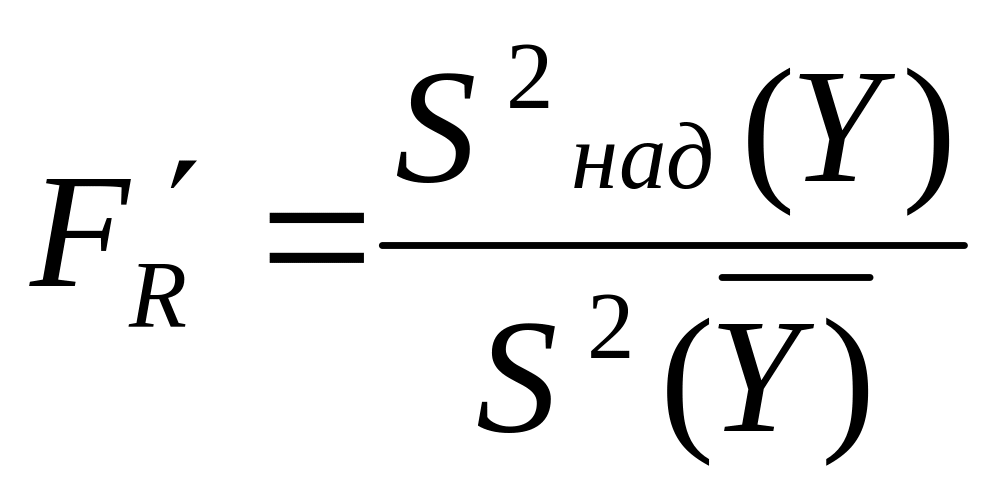Знаходімо табличне значення критерію Фішера за умови:

PD = 0,95

число ступенів волі для більшої дисперсії:

число ступенів волі для меншої дисперсії:

У цьому випадку FT = 245,8.

По розрахунках видно, що < = 2,285 < 245,8; < = 1,45 < 3,95, отримана регресія адекватна < = 2,2 < 5,81.

2.5. Обробка результатів експерименту

Графічна інтерпретація результатів розрахунків зображена на малюнках. У таблиці 2.1 значення факторів і матриць кодувалося з ціллю спрощення записів розумів експерименту та обробки експериментальних даних. Маючи значення основного рівня факторів та інтервалу їх варіювання, починаємо побудову графіків.

РБФМ має вигляд:

= 104,5 – 3X1 – 5,5X2 + 11,5X3 – X1X3 – X2X3 - X1X2X3

Для знаходження наступних точок побудови використовуємо формулу:

;

де Хi – кодоване значення i-го чинника;

Х – натуральне значення i -го чинника;

Хoi – натуральне значення основного рівня i -го чинника;

Ii – інтервал варіювання i -го чинника.

1. Вплів середньої масодовжини котоніну на обривність льнобавовняної пряжі.

= 104,5 – 3X1

Методичні вказівки по виконанню курсової роботи в Excel

Дана методична вказівка складена виходячи з того що студенти вивчають курс мають первинні навики роботи з персональним комп'ютером, табличним процесором Excel. Для ефективної роботи студенти повинні уміти вводити формули в осередки, змінювати колір осередків, шрифт, розрізняти відносні і абсолютні посилання у формулах, а також будувати і редагувати діаграми.

Короткі теоретичні відомості по застосуванню функцій Excel при виконанні курсової роботи

З агальні рекомендації. Для спрощення роботи з даними при виконанні лабораторної роботи необхідно винести на панель інструментів деякі команди. Перш за все, це команда Формат осередки. Щоб її винести необхідно зайти в меню Сервіс-Настройка і відкрити вкладку Команди. На цій вкладці є можливість вибрати необхідні команди і простим рухом миші перетягнути їх на панель інструментів. Виберіть в категорії Формат команду Осередку і перетягнете на панель інструментів. Якщо вставка можлива, то біля перетягуваної команди з'явитися знак +. Для полегшення аналізу даних приведених на розрахунковому листі рекомендується виділяти різним кольором осередку в яких знаходяться початкові і розраховані значення.

Посилання на осередки і діапазони осередків.

Посилання указує на осередок або діапазон осередків листа і передає в Microsoft Excel зведення про розташування значень або даних, які потрібно використовувати у формулі. За допомогою посилань можна використовувати в одній формулі дані, що знаходяться в різних частинах листа, а також використовувати в декількох формулах значення одного осередку. Крім того, можна задавати посилання на осередки інших листів тієї ж книги і на інші книги. Посилання на осередки інших книг називаються зв'язками.

Відносні посилання. Відносне посилання у формулі, наприклад A1, заснована на відносній позиції осередку, що містить формулу, і осередок, на який указує посилання. При зміні позиції осередку, що містить формулу, змінюється і посилання. При копіюванні формули уздовж рядків і уздовж стовпців посилання автоматично коректується. За умовчанням в нових формулах використовуються відносні посилання. Наприклад, при копіюванні відносного посилання з осередку B2 в осередок B3, вона автоматично змінюється з =A1 на =A2.

Абсолютні посилання. Абсолютне посилання осередку у формулі, наприклад $A$1, завжди посилається на осередок, розташований у визначеному місці. При зміні позиції осередку, що містить формулу, абсолютне посилання не змінюється. При копіюванні формули уздовж рядків і уздовж стовпців абсолютне посилання не коректується. За умовчанням в нових формулах використовуються відносні посилання, і для використання абсолютних посилань треба вибрати відповідний параметр. Наприклад, при копіюванні абсолютного посилання з осередку B2 в осередок B3, вона залишається колишньою =$A$1.

Змішані посилання. Змішане посилання містить або абсолютний стовпець і відносний рядок, або абсолютний рядок і відносний стовпець. Абсолютне посилання стовпців набуває вигляду $A1, $B1 і так далі Абсолютне посилання рядка набуває вигляду A$1, B$1 і так далі При зміні позиції осередку, що містить формулу, відносне посилання змінюється, а абсолютне посилання не змінюється. При копіюванні формули уздовж рядків і уздовж стовпців відносне посилання автоматично коректується, а абсолютне посилання не коректується. Наприклад, при копіюванні змішаного посилання з осередку A2 в осередок B3, вона змінюється з =A$1 на =B$1.