§ 8. Закон Дарси для анизотропных сред

Рассмотрим особенности фильтрационных течений в средах, обла­дающих сложной геометрией порового пространства и анизотропией фильтрационных свойств.

В зависимости от структурных особенностей и геометрии порового пространства различают однородные и неоднородные, изотропные и ани­зотропные среды. Анизотропия свойств (в том числе и фильтрационных) означает неодинаковость физических или геометрических свойств по раз­личным направлениям (термин происходит от двух греческих слов: anisos - неравный и tropos - свойства). В реальных коллекторах нефти и газа анизотропия может быть обусловлена трещиноватостью, слоистостью, наличием различного вида включений в коллекторах, которые приводят к неодинаковости свойств по различным направлениям, например в слои­стых пористых средах фильтрационные свойства в плоскости слоев отли­чаются от фильтрационных свойств в направлении, перпендикулярном слоям; в трещиновато-пористых средах фильтрационные потоки по тре­щинам значительно превосходят потоки в других направлениях и т. п.

Для описания фильтрационных течений в анизотропных коллекторах углеводородного сырья постулируется обобщенный закон Дарси, справед­ливость которого подтверждена как многочисленными эксперименталь­ными, так и теоретическими исследованиями. Обобщение закона Дарси на случай анизотропных сред производится, с математической точки зрения, формально. Так как закон Дарси постулирует линейную зависимость меж­ду двумя векторными полями - вектора скорости фильтрации и вектора градиента фильтрационного давления, то соотношения (1.16)÷(1.18) задают наиболее простую зависимость, когда оба вектора лежат на одной прямой отличаются друг от друга направлением и длиной. Такая зависимость определяет и задает изотропные фильтрационные свойства. В общем слу­чае линейная зависимость между двумя векторными полями определяется таким образом, что каждая компонента одного вектора зависит от всех компонент другого. Поэтому в самом общем случае линейная зависимость вектора скорости фильтрации и градиента фильтрационного давления (са­мый общий случай закона Дарси для анизотропных сред) имеет следую­щий вид:

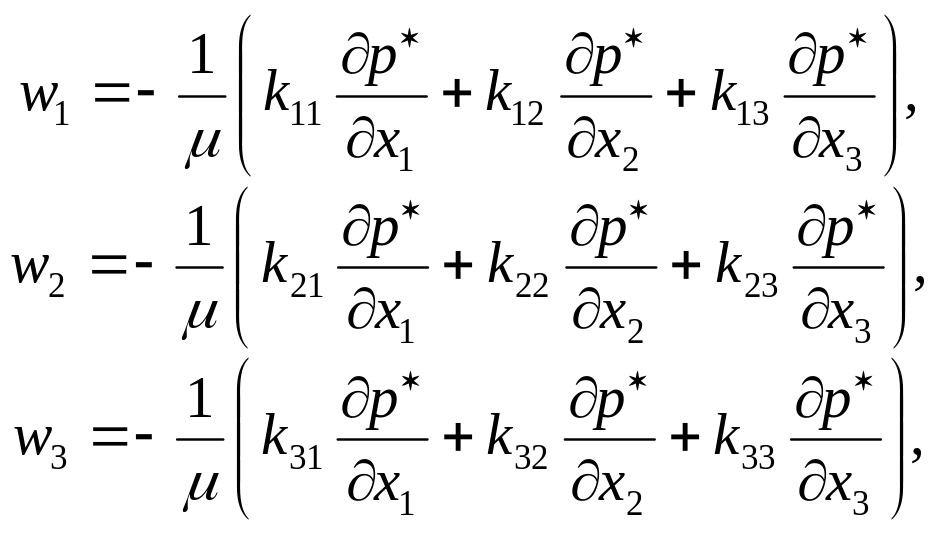(1.48)

где w_i - компоненты вектора скорости фильтрации, - компоненты вектора градиента приведенного давления, k_ij (i = 1, 2, 3, j = 1, 2, 3) - компо­ненты симметричной матрицы (тензора¹), которая называется матрицей (тензором) коэффициентов проницаемости. Она определяет и задает фильтрационные свойства пористой среды, которые могут быть как изо­тропными, так и анизотропными, с разными типами анизотропии. Явный вид матрицы коэффициентов проницаемости зависит от типа анизотропии и системы координат, в которой записан обобщенный закон Дарси. Всегда можно выбрать хотя бы одну систему координат Ox₁x₂x₃, в которой запись обобщенного закона Дарси имеет наиболее простой вид:

(1.49)

Соотношение (1.48) может быть записано и в матричном виде:

(1.50)

Если принять соглашение о суммировании, согласно которому по повторяющемуся в записи индексу подразумевается суммирование, то со­отношение (1.48) можно записать более компактно:

(1.51)

где i и j принимают значения 1, 2, 3.

Система координат, в которой матрица коэффициентов проницаемо­сти имеет диагональный вид и обобщенный закон Дарси записывается в виде (1.49), называется главной системой координат, а значения диаго­нальных коэффициентов проницаемости k_i - главными значениями тензо­ра проницаемости. В главной системе координат компоненты матрицы обозначаются одним индексом, если система координат не главная — дву­мя. Первый индекс соответствует номеру строки, второй — столбца.

В соотношении (1.51) выписано самое общее представление закона Дарси для анизотропных пористых сред. Уменьшая число отличных от ну­ля компонент матрицы коэффициентов проницаемости, можно получить все возможные типы анизотропии и даже изотропию. В самом деле, если положить, что все недиагональные элементы матрицы равны нулю, а все диагональные равны друг другу, то получим изотропные свойства. Все ос­тальные варианты будут задавать разные типы анизотропии. Прежде чем их классифицировать, определим свойство проницаемости в самом общем виде.

Проницаемостью пористой среды, по определению (или направ­ленной проницаемостью) называется величина , которая опреде­ляется по формуле:

(1.52)

где n_i - единичный вектор, задающий направление в пористой среде, вдоль которого определяется направленная проницаемость, - скаляр­ное произведение вектора скорости фильтрации и единичного вектора, - модуль градиента фильтрационного давления. Как следует из оп­ределения, в общем случае проницаемость может зависеть от направления.

Определение (1.52) имеет прозрачный физический смысл - прони­цаемость, по определению, является скалярной величиной, которая вычис­ляется вдоль некоторого направления. Поэтому, для того чтобы ее вычис­лить, необходимо найти отношение скалярных величин, специальным обра­зом определенных вдоль направления. В равенстве (1.52) в качестве направ­ления, вдоль которого определяется свойство, по определению, рассматри­вается направление приложения градиента давления: , а скалярные величины определяются проектированием на это направление векторов скорости фильтрации и градиента фильтрационного давления. При проектиро­вании на это направление векторов и получаем w_in_i и , а их отноше­ние, умноженное на вязкость и взятое с об­ратным знаком, равно проницаемости. Знак минус берется потому, что скалярное про­изведение w_in_i отрицательно (угол между векторами и , тупой). Иллюстрация опре­деления направленной проницаемости при­ведена на рис. 1.16.

Подставляя запись обобщенного на случай анизотропных сред зако­на Дарси (1.51) в равенство (1.52), получим:

(1.53)

Соотношение (1.53) дает общее правило вычисления проницаемости, кото­рое справедливо как для изотропных, так и для анизотропных пористых сред. В самом деле, для изотропных пористых сред, по определению (1.52) и правилу (1.53) вычисления проницаемости в линейном законе фильтра­ции, имеем

Следовательно, проницаемость для изотропных сред не зависит от направ­ления (она для всех направлений одинакова и равна k).

Равенство (1.53) расшифровывает и смысл утверждения, согласно которому матрица коэффициентов проницаемости k_ij определяет и задает фильтрационные свойства пористой среды. В самом деле, вид матрицы оп­ределяет тип свойства - изотропные или анизотропные, а численные зна­чения - величину.

Как было показано, изотропные фильтрационные свойства задаются матрицей вида:

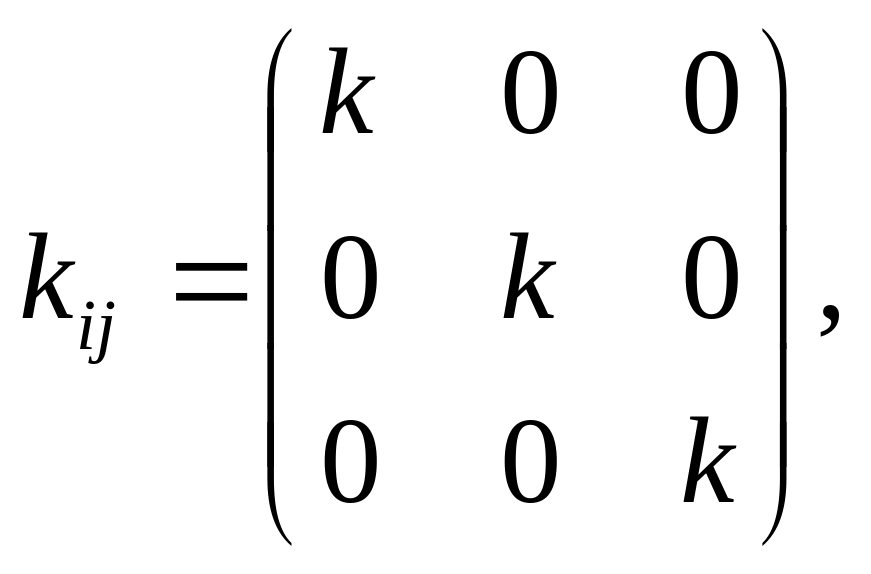(1.54)

следовательно, все возможные другие типы матриц задают анизотропные фильтрационные свойства. С помощью методов линейной алгебры можно показать, что все возможные варианты «анизотропных» матриц имеют вид:

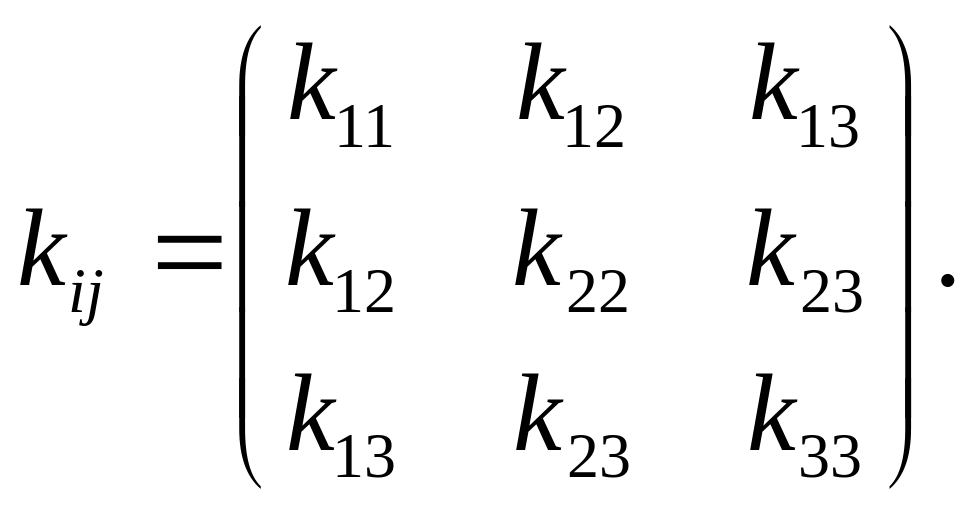(1.55)

Первый тип матриц (1.55) задает фильтрационные свойства, напри­мер, слоистых (как правило, осадочных) пористых сред, у которых прони­цаемость в поверхностях напластований одинакова (плоскость с изотроп­ными фильтрационными свойствами) и отличается от проницаемости в на­правлении, перпендикулярном к поверхностям напластований. Так как матрица имеет диагональный вид, то главные направления тензора коэф­фициентов проницаемости у данного типа пористых сред известны априо­ри - одно главное направление перпендикулярно слоистости, два других - лежат в плоскости слоистости. В представлении матрицы коэффициентов проницаемости (1.54) направление, перпендикулярное напластованию, со­ответствует координатной оси Ох₃.

Рис. 1.16. Схема к определе­нию направленной прони­цаемости

Второй тип анизотропии задает пористую или трещиноватую среду, у которой априори, как и в первом случае, известны направления всех главных осей матрицы k_ij, но проницаемости по всем главным направле­ниям различны. Подобной анизотропией могут обладать трещиноватые коллекторы с тремя взаимно перпендикулярными системами трещин или уже упомянутые осадочные породы, образованные частицами вытянутой формы.

Первые два типа анизотропии имеют специальные названия - пер­вый тип называется трансверсально-изотропным, второй — ортотропным.

В оставшихся двух типах анизотропии априори неизвестно положе­ние главных осей. В третьем типе неизвестно положение двух главных осей, в последнем случае неизвестно положение всех трех главных осей. По-видимому, реальные пористые и трещиноватые среды, как правило, к этим типам и относятся, но при решении задач обычно рассматриваются два первых. Специальных названий два последних типа не имеют. Подста­новка матриц (1.55) в равенство (1.50) даст явный вид закона Дарси для всех типов анизотропии.

Равенства (1.48) представляют собой систему линейных алгебраических уравнений, которая может быть разрешена относительно компонент и переписана в виде

Контрольные вопросы и задачи

1. Каковы особенности теории фильтрации по сравнению с гидромехани­кой в открытом пространстве?

2. При фильтрации жидкости с постоянным расходом через несцементи­рованную пористую среду произошло вымывание мелких фракций песка. Изменились ли при этом скорость фильтрации и средняя ско­рость движения жидкости?

3. Куб с ребром 1 м наполнили шарами диаметром 10 см каждый, а куб с ребром 1 см точно так же уложили шарами диаметром 1 мм каждый. Пористость какой засыпки больше?

4. Показать, что если образец пористого материала, имеющий объем V и пористость т, разбить на п частей объемом V_i (i = 1,...,п), то

где т_i - пористость i-й части. Рассмотреть случай, когда все V_i оди­наковы.

5. Каковы физические причины нарушения закона Дарси и при каких условиях он выполняется?

6. Определить удельную поверхность фиктивного грунта, пористость ко­торого т = 0,25, а диаметр шаров равен 0,2 мм.

Найти также число шаров в 1 м³.

7. Определить пористость, удельную поверхность и просветность для рыхлой кубической упаковки шаров.

8. Определить пористость для кубической и гексагональной упаковок шаров.

9. Определить коэффициент проницаемости пористой среды (в м² и Дар­си), если известно, что коэффициент фильтрации k_ф=0,3∙10^-4 см/с, а кинематический коэффициент вязкости жидкости v = 10^-6 м²/с.

10. Определить проницаемость при фильтрации через образец площадью 1 см², при перепаде давления 1 кгс/см² с расходом жидкости 1 см³/с, если длина образца равна 1 см, а фильтрующаяся жидкость имеет ди­намический коэффициент вязкости 1 сП (один сантипуаз).

Решение. Разрешим равенство (1.7) относительно коэффициента прони­цаемости:

Переведем все единицы измерения в систему СИ — 1см² = 10^-4м², 1 кгс/см² = 98 кПа, 1 см³/с = 10^-6 м³/с, 1см =10^-2м, и вязкость в один санти­пуаз (μ = 1 сПа) в системе СИ равняется 1 мПа/с. После подстановки чис­ленных данных в формулу получим

Сравнение полученного результата с переводным коэффициентом от еди­ницы измерения 1 Дарси к 1 метру в квадрате показывает, что вычисленная по условию задачи проницаемость равна одному Дарси. Таким образом, в условии задачи дано определение единицы проницаемости в один Дарси.

11. Определить коэффициент фильтрации для керна, помещенного под уг­лом α к горизонгу, если массовый расход жидкости равен Q_M, плот­ность жидкости и вязкость равны, соответственно, ρ и μ, а разница напоров в начале и в конце керна составляет ΔН, площадь сечения равна Ω, длина керна - L.

12. Образец пористой среды длиной 10 см и диаметром 5 см после насы­щения под вакуумом керосином с плотностью 810 кг/м³ стал тяжелее

на 20 г. Определить коэффициент пористости образца.