§ 4. Опыт и закон Дарси. Проницаемость. Понятие «истинной» средней скорости и скорости фильтрации

Обратимся теперь к движению жидкости в пористой среде. Первые экспериментальные наблюдения за движением воды в трубах, заполнен­ных песком, произвели А. Дарси (1856 г.) и Ж. Дюпюи (1848-1863 гг.). Этими работами было положено начало теории фильтрации. Именем Дар­си назван линейный закон фильтрации, который он установил, создавая первую совершенную систему водоснабжения в Европе.

Анри Дарси исследовал течение воды через вертикальные песчаные фильтры (рис. 1.5), которые требовались для водоснабжения города Дижона. В результате тщательно проведенных экспериментов была установлена получившая широкую известность экспериментальная формула

(1.6)

где Q — объемный расход жидкости через песчаный фильтр, длина которо­го L, а площадь сечения S, ΔH = H₁- Н₂ - разность гидравлических на­поров воды над фильтром и у его основания, k_ф - коэффициент пропор­циональности. Коэффициент пропорциональности в формуле (1.6) перво­начально был назван коэффициентом водопроницаемости, а затем коэф­фициентом фильтрации, который зависит как от природы пористой сре­ды, так и свойств фильтрующейся жидкости. Как уже отмечалось, скоро­сти фильтрации очень малы (порядка 10^-4÷10^-5 м/с и менее), поэтому ско­ростными напорами при вычислении гидравлических напоров в равенст­ве (1.6) пренебрегают:

(1.7)

В равенстве (1.7) используются общепринятые в технической гидромеха­нике обозначения: v_a — средние скорости в капилляре, α_i - коэффициенты Кориолиса (в нашем случае α₁ = α₂ = 2), р - давление, z - геометрический напор, ρ - плотность жидкости, g — ускорение свободного падения.

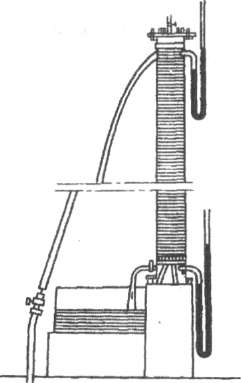
Рис. 1.5. Установка Анри Дарси для исследования те­чения воды через вертикальные песчаные фильтры

Коэффициент фильтрации, как следует из равенства (1.7), име­ет размерность скорости и характеризует скорость потока через единицу площади сечения, перпендикулярного к потоку, под действием единичного градиента напора.

Коэффициент фильтрации k_ф используется обычно в гидротехниче­ских расчетах, где приходится иметь дело с одной жидкостью - водой. При исследовании фильтрации газа, нефти и их смесей необходимо разделить влияние свойств пористой среды и флюида. Поэтому для разделения свойств флюида и пористой среды равенство (1.6) представляют в ином виде:

(1.8)

или

(1.9)

где μ - динамический коэффициент вязкости, р* = ρgH = р + ρgz - при­веденное давление, k — коэффициент проницаемости, который не зави­сит от свойств жидкости и является динамической характеристикой только пористой среды. Размерность коэффициента проницаемости оп­ределяется из следующей формулы:

и равна размерности площади, то есть в системе единиц измерения СИ — метр в квадрате. Проницаемость большинства горных пород выражается весьма малыми числами. Так, проницаемость крупнозернистых песчаников составляет 10^-12÷10^-13 м² (1÷0,1 мкм²), проницаемость плотных песчани­ков — 10^-14 м² (0,01 мкм²). Ввиду этого в нефтепромысловой практике полу­чила распространение единица измерения проницаемости 1Д (Дарси) = 1,02·10^-12 м².

Из сравнения равенств (1.6) и (1.8) следует, что коэффициент фильт­рации и проницаемости связаны между собой соотношением вида:

(1.10)

Коэффициент фильтра­ции k_ф или коэффициент про­ницаемости k определяют экс­периментально на специальном приборе - пермеаметре, содер­жащем образец исследуемого грунта (рис. 1.6). Общий расход Q фильтрационного потока поддерживается постоянным, напоры Н₁ и Н.₂ измеряются двумя пьезометрами, соединен­ными с пористой средой в сечениях 1 и 2. Превышение центров сечений над плоскостью сравнения равны z₁ и z₂, а давления - р₁ и р₂; расстояние между сечениями по оси цилиндра составляет L.

В соответствии с формулой (1.6) или (1.8) имеем

или

где перепад напора, приходящийся на единицу длины (модуль градиента давления), можно представить в следующем виде:

Рис. 1.6. Схема пермеаметра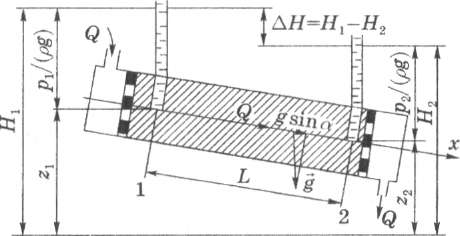

В промысловых условиях коэффициент проницаемости определяется в результате специального исследования скважин, в котором также ис­пользуется устанавливаемая в опыте связь между изменением давления в скважинах и их дебитом.

Обычно соотношения (1.6) или (1.9) называют законом Дарси. Одна­ко эти соотношения представляют собой следствие из закона Дарси — ре­шение одной из простейших задач одномерного течения, реализуемого в пермеаметре или установке типа установки А. Дарси, сам же закон Дарси связывает между собой вектор скорости фильтрации и градиент фильтрационного давления и будет рассмотрен далее, после введения понятия скорости фильтрации.

Разделим обе части равенства (1.9) на площадь сечения S и получим

(1.11)

Выражение w = Q/S имеет размерность скорости и определяет модуль вектора скорости фильтрации. При определении расхода считается, что вектор скорости фильтрации направлен перпендикулярно плоскости (галерее), через которую фильт­руется флюид (рис. 1.7). Поэтому если через - обозначить единичный вектор, перпендикулярно поверхности (или параллельно ско­рости), то будем иметь . Отличие вектора от обычной скорости состоит в том, что скорость фильтра­ции — фиктивная скорость, так как она, по своему смыслу, определена в любой точке сечения пористой среды – и в порах, и в твердом скеле­те, в то время как на самом деле течение происходит только по поровым каналам с некоторой «истинной средней скоростью» . Понятно, что меж­ду скоростями и существует связь, которая следует из равенства рас­хода, протекающего с истинной средней скоростью через площадь просве­тов, и всё сечение в целом со скоростью фильтрации

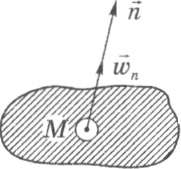
Рис. 1.7. Схема к определению и скоросги фильтрации

из последнего равенства следует

(1.12)

Таким образом, скорость фильтрации равна истинной средней скоро­сти, умноженной на просветность. Но заменять просветность на порис­тость в равенстве (1.12) теоретически неправомерно.

Для доказательства сделанного утверждения рассмотрим следующие рассуждения. Соотношение (1.12) так же, как и равенства (1.8) и (1.9), справедливо в предположении, что фильтрационные свойства пористой среды изотропные и однородные, то есть проницаемость не зависит от на­правления и постоянна для всех точек. Если положить, что пористая среда однородная, но анизотропная, то можно проделать следующий экспери­мент. Вырежем куб, грани которого будут перпендикулярны главным на­правлениям проницаемости (то есть при приложении градиента давления перпендикулярно граням куба, векторы скорости фильтрации также будут перпендикулярны граням куба). Введем декартову систему координат, оси которой будут направлены вдоль ребер куба, и проделаем серию экспери­ментов, направляя скорость фильтрации последовательно вдоль каждой оси. В результате, для каждого эксперимента, получим:

где w_x, w_y, w_z - компоненты вектора скорости фильтрации, Q_x, Q_y, Q_z, и k_x, k_y, k_z - значения расходов и проницаемости вдоль соответствующих ко­ординатных осей. Таким образом, при одинаковых перепадах давления и площади сечения образца, в общем случае, необходимо вводить разные значения просветности при построении связи между скоростями фильтра­ции и средними истинными скоростями:

или

(1.13)

где v_x, v_y, v_z и s_x, s_y, s_z, - значения истинных средних скоростей и просвет­ности вдоль соответствующих координатных осей. В самом деле, связь (1.12) задает линейную зависимость между двумя векторами, которая в наиболее общем виде, для записи в главных осях, задается формулой:

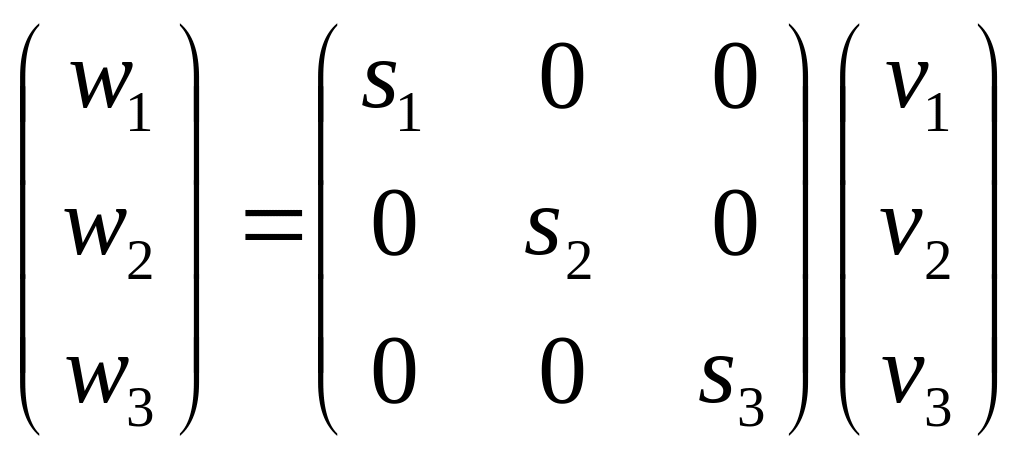(1.14)

Частный случай равенства (1.14) - s₁ = s₂ = s₃ = s приводит к соот­ношению (1.12), в общем — имеем матрицу коэффициентов просветности.

Таким образом, при переходе от средних истинных скоростей к ско­ростям фильтрации необходимо использовать даже не скалярную функцию векторного аргумента, которая выше была определена как просвегность, а матрицу.

Переход от экспериментального соотношения (1.9) к равенству (1.11) показывает, что в эксперименте Анри Дарси была установлена линейная зави­симость между двумя векторными характеристиками - вектором скорости фильтрации и вектором градиента фильтрационного давления в однород­ной изотропной недеформируемой пористой среде. Однако равенст­во (1.11) представлено в скалярном виде, поэтому восстановим его в векторной форме записи.

В случае изотропных фильтрационных свойств векторы скорости фильтрации и градиента фильтрационного давления лежат на одной пря­мой. Поэтому, если умножим равенство (1.9) на орт , задающий направ­ление фильтрации, получим:

(1.15)

В равенстве (1.15) множитель представляет собой модуль градиента приведенного давления при линейном законе распределения давления. Следовательно, дальнейшее обобщение экспериментального результата приводит к векторному уравнению вида

(1.16)

Векторное уравнение (1.16) представляет собой закон Дарси для изотропной пористой среды. Знак минус в правой части равенства появ­ляется из-за того, что скорость фильтрации направлена в сторону умень­шения приведенного давления. Поэтому векторы скорости фильтрации и градиента фильтрационного давления направлены в разные стороны (на­помним, градиент направлен в сторону роста давления, а скорость фильт­рации, следовательно, в обратную сторону — от большего давления к меньшему).

Равенство (1.16) задает закон Дарси в универсальной безиндексной форме записи, справедливой для любой системы координат. В декартовой системе координат равенство записывается в виде:

(1.17)

где i, j, k - орты декартовой системы координат, при этом ось z направлена вертикально вверх. Последнее векторное равенство может быть спроекти­ровано на оси координат и переписано в виде системы уравнений:

(1.18)