§ 7. Нелинейные законы фильтрации

Как было показано в предыдущем параграфе, основное уравнение теории фильтрации, закон Дарси, имеет верхнюю и нижнюю границы применимости, поэтому необходимо его обобщение.

Таблица 1.2. Интервалы критических значений Re для образцов пористых сред

№ п/п	Образец пористой среды	Диапазон крити­ческих значений
1	Однородная дробь	13-14
2	Однородный крупнозернистый песок	3-10
3	Неоднородный мелкозернистый песок с преобла­данием фракций диаметром менее 0,1 мм	0,34-0,23
4	Сцементированный песчаник	0,05-1,4

Первое обобщение закона Дарси при Re ≥ Re_кр было предложено Дюпюи, который сформулировал двухчленный закон, получивший имя австрийского ученого Ф. Форхгеймера, независимо предложившего этот закон несколько позднее. Двучлен­ный закон, разрешенный относительно градиента давления, в векторной форме записывается в виде

(1.38)

где w - модуль вектора скорости фильтрации, β - константа пористой среды, определяемая экспериментально. Для одномерного течения, когда модуль градиента давления изменяется линейно (см. § 4, формула (1.15)), уравнение можно спроектировать на координатную ось и записать в ска­лярном виде

(1.39)

Из вида последнего равенства становится понятно, почему обычно соотношение (1.38) трактуется как разложение в ряд Тейлора закона фильтрации по степеням вектора скорости фильтрации. Однако представ­ление является аппроксимацией экспериментальных результатов с помо­щью функции f (w) = а + bw

Необходимо отметить, что представление нелинейного закона фильт­рации в виде (1.38) является не единственным. В учебниках и монографиях приводится и иное представление коэффициента при квадратичном члене. Например, вместо константы/? и проницаемости фигурирует коэффициент макрошероховатости I, введенный Е.М. Минским,

или иной коэффициент проницаемости (коэффициент проницаемости ве­сомой жидкости),

где k_μ - коэффициент проницаемости для вязкой жидкости, k_ρ — коэффи­циент проницаемости весомой жидкости.

Более того, как уже отмечалось выше, кроме нефтегазовой отрасли задачи фильтрации рассматриваются и в других отраслях промышленно­сти - в машиностроении, в химической технологии, в авиации, и т.д. И в каждой из отраслей для представления нелинейного закона фильтрации предлагаются свои формулы и зависимости. Например, в химической тех­нологии получила широкое распространение формула Эргуна. Формула Эргуна предложена для расчетов нелинейных фильтрационных течений в фиктивных пористых средах, образованных упаковками шаров постоянно­го диаметра, и имеет следующий вид:

(1.40)

Понятно, что соотношение (1.40) представляет собой нелинейный за­кон фильтрации типа Форхгеймера (1.38), записанный для одномерной фильтрации вдоль оси Ох (1.39). Поэтому представляет интерес анализ ма­териальных коэффициентов, стоящих множителями при скорости фильтра­ции в первой и второй степени.

Нетрудно заметить, что в формуле Эргуна коэффициент при первой степени скорости представляет собой отношение μ/k, где проницаемость определяется формулой

(1.41)

которая получается из формулы (1.26) при значении с=4,17.

Для того чтобы можно было интерпретировать выражение (1.41) со значением с=4,17, необходимо привести следующие данные. Изначально число Кармана было принято универсальным и равным пяти. Дальнейшими исследованиями было установлено, что оно не является универсальным и для фиктивных пористых сред изменяется согласно теоретическим вычис­лениям в диапазоне от 4,54 до 7,22 (при пористости, изменяющейся в пре­делах от 0,34 до 0,459) и согласно экспериментальным исследованиям от 4,5 до 5,1 (при пористости, изменяющейся в пределах от 0,4 до 0,6). Поэто­му значение числа Кармана в формуле Эргуна принимается лишь для одно­го значения пористости, которое при этом близко к наиболее плотным упа­ковкам шаров.

Формулы, аналогичные формуле Эргуна, имеют место при решении прикладных задач в других отраслях промышленности. Например, в маши­ностроении для нелинейной фильтрации в упаковках шаров используется формула вида

(1.42)

Нетрудно видеть, что коэффициенты при первой степени скорости фильтрации в формуле Эргуна и в (1.42) отличаются только значением численного множителя. Для обобщения представлений (1.40) и (1.42) мож­но аппроксимировать значение числа Кармана по экспериментальным дан­ным.

Изначально число Кармана с представлялось в виде композиции ко­эффициента формы и квадрата коэффициента извилистости. Однако в дальнейшем было показано, что с представляется в виде композиции ко­эффициентов структуры φ и формы f. Для представления указанных ко­эффициентов как функций от пористости, используя экспериментальные данные, можно получить следующие выражения:

и

Поэтому для с имеем

(1.43)

Как уже было отмечено выше, для наиболее плотных упаковок шаров пористость изменяется в интервале от 0,259 до 0,476. На этом интервале пористости значение числа Кармана по формуле (1.43) изменяется от 3,975 до 5,227, а значения коэффициента, стоящего численным множителем при первой степени скорости фильтрации при представлении проницаемости - по формуле (1.26) — от 143,1 до 183,2. Таким образом, значения численных коэффициентов в формулах (1.40) и (1.42) лежат в приведенном диапазоне, и формулы не учитывают изменение значения числа Кармана от пористо­сти.

Подстановка соотношения (1.43) в формулу Эргуна приводит к сле­дующей ее модификации:

(1.44)

Заметим, что в формуле (1.44) учитывается изменение числа Кармана как функции от пористости, что фактически означает учет изменения структуры порового пространства фиктивных пористых сред. Аналогичный учет структуры, очевидно, необходим и для коэффициента, стоящего мно­жителем при w². Однако для подобного анализа необходимо проведение дополнительных, как теоретических, так и экспериментальных исследова­ний.

Представление (1.38) - лишь один из вариантов обобщения закона Дарси при больших скоростях фильтрации. Другой распространенный ва­риант нелинейного закона фильтрации, разрешенного относительно скоро­сти фильтрации, имеет вид

(1.45)

где - модуль вектора градиента фильтрационного давления, а, п - материальные константы пористой среды, определяемые в результате об­работки экспериментальных данных. Обычно константа п лежит в преде­лах от единицы до двух. При п = 2 формула (1.45) называется формулой Краснопольского, который положил, что при отклонении от закона Дарси зависимость между градиентом давления и скоростью фильтрации квадра­тичная. В самом деле, для одномерного течения уравнение (1.45) можно спроектировать на координатную ось и записать в скалярном виде

и при п = 2 получаем

Соотношение (1.38) представляется более универсальным, чем (1.45), и обычно считается, что его можно использовать при любых скоро­стях фильтрации. Просто при малых скоростях фильтрации второе слагае­мое имеет второй порядок малости по скорости фильтрации и им можно пренебречь. В то время как степенной закон фильтрации (1.45), очевидно, можно использовать только при нарушении закона Дарси (то есть при Re ≥ Re_кр).

Введение в представление множителя при второй степени скорости фильтрации в формуле (1.38) плотности ρ следует как из теории размер­ности, так и из физического смысла, вкладываемого в причину отклонения закона фильтрации от линейности (мера инерции - масса, умноженная на ускорение, плотность — удельная масса).

Для изотропных пористых сред несложно получить общий вид нели­нейного закона фильтрации. Умножим закон Дарси скалярно вначале на скорость фильтрации, а потом на градиент фильтрационного давления. В результате получим следующие равенства:

и

После подстановки правой части второго равенства в первое и извлечения из обеих частей полученного равенства квадратного корня, будем иметь

Далее, разрешая последнее равенство относительно k, получим

(1.46)

В эксперименте находится зависимость . По­этому, выбрав класс функций, в которых определяется аппроксимация , можно построить тот или иной нелинейный закон фильтрации.

Аналогичные выкладки и рассуждения можно проделать и при опреде­лении закона фильтрации, разрешенного относительно градиента фильтра­ционного давления. Выражение, аналогичное (1.46), для коэффициента фильтрационного сопротивления имеет вид

В этом случае полученная экспериментальная зависимость обрабатывается уже как

Однако, как было отмечено выше, отклонения от закона Дарси экс­периментально наблюдаются не только при больших, но и малых скоро­стях фильтрации (так как скорости фильтрации очень малы, то это откло­нения вблизи нуля). Отклонения при малых скоростях фильтрации имеют другую физическую природу и обусловливаются неньютоновскими свой­ствами жидкости и большими поверхностными силами (силами взаимо­действия между флюидом и твердым скелетом). При очень малых скоро­стях фильтрации неньютоновскими свойствами в пористой среде могут обладать даже ньютоновские жидкости. Но с ростом скорости этот эффект в ньютоновских жидкостях исчезает. В нефтегазовом деле к жидкостям, проявляющим неньютоновские свойства, относятся аномальные нефти и буровые растворы.

Классическим примером закона фильтрации для неньютоновской жидкости является закон фильтрации с предельным (начальным) градиен­том. Этот закон фильтрации выписывается для вязкопластичной жидкости Бингама-Шведова и имеет вид

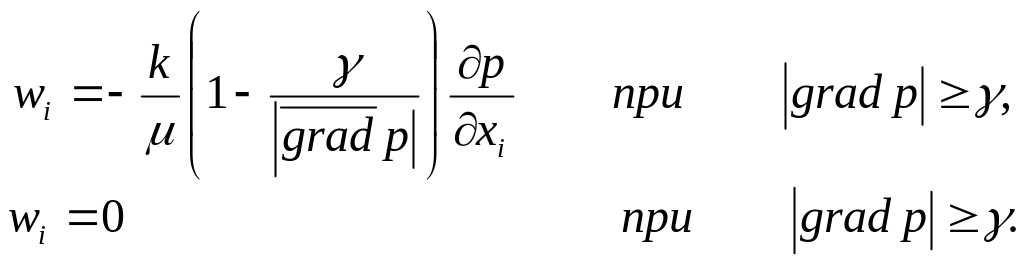(1.47)

Как следует из соотношений (1.47), фильтрационное течение воз­можно лишь при градиентах давления, превышающих некоторое значе­ние γ, которое называется начальным (предельным) градиентом. При меньших значениях градиента давления фильтрационное течение отсутствует. Величина начального градиента зависит от начального напряжения сдвига жидкости τ₀ и эффективного диаметра капилляра d_эф. На рисун­ке 1.15 приведены графики зависимости скорости фильтрации от градиен­та фильтрационного давления, которые соответствуют линейным и нели­нейным законам фильтрации.

Рис. 1.15. Графики зависимости w от |grad р|

1. - для ВПЖ с предельным градиентом;

2. - для реальных неньютоновских нефтей;

3. - зависимость по закону Дарси