
- •Графики функций
- •Оглавление
- •Часть 1. Построение эскизов графиков функций 4
- •Часть 2. Применение дифференциального исчисления к исследованию функций и построению их графиков 38
- •Введение
- •Часть 1. Построение эскизов графиков функций
- •1. Графики основных элементарных функций
- •1.1. Постоянная и степенная функции
- •1.2. Показательная и логарифическая функции
- •1.3. Тригонометрические функции
- •1.4. Обратные тригонометрические функции
- •2. Элементарные преобразования графиков
- •3. Построение графиков функций, не являющихся элементарными
- •4. Действия с графиками функций
- •4.1. Сложение и вычитание графиков
- •4.2. Умножение и деление графиков
- •4.3. Построение графиков сложных функций
- •5. Графики в полярных координатах
- •5.1. Полярные координаты
- •5.2. Графики кривых в полярных координатах
- •Часть 2. Применение дифференциального исчисления к исследованию функций и построению их графиков
- •1. Признак возрастания и убывания функции
- •2. Локальные экстремумы функции
- •3. Выпуклость функции. Точки перегиба
- •4. Асимптоты
- •5. Порядок построения графика функции, заданной выражением
- •6. Построение графика функции, заданной параметрически
- •6.1. Порядок построения графика параметрически заданной функции
- •6. 2. Асимптоты параметрического графика
- •6. 3. Точки перегиба
- •6.4. Пример построения графика параметрически заданной функции
- •Список литературы
Часть 2. Применение дифференциального исчисления к исследованию функций и построению их графиков
В этом разделе мы рассмотрим как построить график функции, используя теорию пределов и дифференциальное исчисление.
1. Признак возрастания и убывания функции
Зная производную функции, мы можем выяснить на каком промежутке функция будет возрастать, а на каком убывать. Вспомним сначала определение монотонной функции.
Определение
3. 5
Функция
,
определенная на некотором промежутке
вещественной оси, называется возрастающей
(убывающей)
на этом промежутке, если для любых
![]() и
и
![]() из этого промежутка, таких, что
из этого промежутка, таких, что
![]() выполняется неравенство
выполняется неравенство
![]() (соответственно, неравенство
(соответственно, неравенство
![]() ).
).
Если
функция
возрастает на некотором промежутке, то
функция
![]() ,
получающаяся из
изменением знака у всех ее значений
является убывающей на этом промежутке
функцией.
,
получающаяся из
изменением знака у всех ее значений
является убывающей на этом промежутке
функцией.
Возрастающие и убывающие на некотором промежутке функции называются монотонными на этом промежутке.
Если
в определении 3 при
выполняется строгое неравенство
![]() (соответственно
(соответственно
![]() ), то функция
называется строго
возрастающей (строго убывающей).
), то функция
называется строго
возрастающей (строго убывающей).
Функция, строго возрастающая или строго убывающая, называется строго монотонной.
Очевидно, что строго монотонная (возрастающая, убывающая) функция является и просто монотонной (соответственно возрастающей, убывающей) функцией в смысле определения 3.
Рассмотрим
некоторый интервал
![]() вещественной оси. Сформулируем теорему,
которая содержит необходимое и достаточное
условие возрастания и убывания функции
на интервале
.
вещественной оси. Сформулируем теорему,
которая содержит необходимое и достаточное
условие возрастания и убывания функции
на интервале
.
Теорема
1. 6
Для
того чтобы дифференцируемая на интервале
функция
возрастала (убывала) на этом интервале
необходимо и достаточно, чтобы во всех
его точках производная этой функции
была неотрицательной,
![]() (соответственно, неположительной,
(соответственно, неположительной,
![]() ).
).
Если
всюду на
производная положительна:
![]() (соответственно отрицательна:
(соответственно отрицательна:
![]() ),
то функция
строго возрастает (строго убывает) на
рассматриваемом интервале.
),
то функция
строго возрастает (строго убывает) на
рассматриваемом интервале.
Условия
и
не являются необходимыми для строгого
возрастания, соответственно строгого
убывания, функции, Например, функция
строго возрастает на любом интервале
вещественной оси, но
![]() .
.
Теорема остается верной для непрерывных функций, не имеющих в конечном числе точек производной. Утверждение второй части теоремы остается в силе, если кроме того, в конечном числе точек производная обращается в нуль.
Пример
14.
Найти промежутки возрастания и убывания
функции
![]() .
.
Решение.
Определим производную
![]() :
:
![]()
Очевидно,
что
![]() при любом значении
,
следовательно, функция
возрастает на всей числовой оси.
при любом значении
,
следовательно, функция
возрастает на всей числовой оси.
В
частности, поскольку
![]() ,
то для всех
выполняется неравенство
,
то для всех
выполняется неравенство
![]() или
или
![]()
2. Локальные экстремумы функции
Введем определения локального максимума и минимума функции, а также признаки их существования.
Определение
4. 7
Пусть
функция
определена в некоторой окрестности
точки
.
Точка
называется точкой локального
максимума
(соответственно точкой локального
минимума)
функции
,
если существует такое
![]() ,
что для всех
,
что для всех
![]() удовлетворяющих условию
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() (соответственно
(соответственно
![]() ).
).
Если
существует такое
,
что для всех
![]() ,
таких, что
,
выполняется неравенство
,
таких, что
,
выполняется неравенство
![]() (соответственно
(соответственно
![]() ,
то
называется точкой строгого
локального максимума
(соответственно строгого
локального минимума).
,
то
называется точкой строгого
локального максимума
(соответственно строгого
локального минимума).
Точки (строгого) максимума и минимума называются точками (строгого) экстремума.
Например,
на рис. 33 точки
и
![]() являются точками локального максимума,
а точки
и
являются точками локального максимума,
а точки
и
![]() - локального минимума.
- локального минимума.
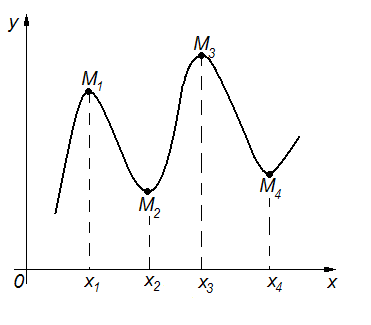
Рис. 33. Экстремумы функции.
Для
точек
строгого экстремума функции
,
и только для них, приращение
![]() не меняет знака при переходе аргумента
через
,
т. е. при изменении знака
.
Именно
не меняет знака при переходе аргумента
через
,
т. е. при изменении знака
.
Именно
![]() для точек строгого максимума и
для точек строгого максимума и
![]() в случае строгого минимума независимо
от знака достаточно малого
.
в случае строгого минимума независимо
от знака достаточно малого
.
Приведем необходимые условия наличия локального экстремума функции.
Теорема
2. 8
(необходимые
условия экстремума). Пусть
является точкой экстремума функции
,
определенной в некоторой окрестности
точки
.
Тогда либо производная
![]() не существует, либо
не существует, либо
![]() .
.
Отметим, что условие не является, для дифференцируемой при функции, достаточным условием наличия экстремума, как это показывает пример функции , которая для имеет производную, равную нулю, но для которой не является точкой экстремума.
Приведем теперь теоремы, содержащие достаточные условия строгого локального экстремума функции в терминах смены знака производной и для функции, имеющей производные высших порядков.
Теорема 3. 9 (достаточные условия строгого экстремума). Пусть функция дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки , в которой, однако, функция непрерывна. Тогда точка является точкой строгого максимума, если существует окрестность точки , в которой при и при .
Если же при и при , то - точка строгого минимума.
Теорема
4. 10
Пусть
в точке
у функции
существуют производные до порядка
![]() включительно, причем
включительно, причем
![]()
Тогда,
если
![]() ,
,
![]() ,
т. е.
,
т. е.
![]() — четное число, то функция
имеет в точке
строгий экстремум, а именно максимум
при
— четное число, то функция
имеет в точке
строгий экстремум, а именно максимум
при
![]() и минимум при
и минимум при
![]() .
Если же
.
Если же
![]() ,
,
т. е.
- нечетное число, то функция
не имеет в точке
экстремума.
,
,
т. е.
- нечетное число, то функция
не имеет в точке
экстремума.
Следствие.
11
Если
,
а
![]() ,
то при
,
то при
![]() является точкой строгого минимума, а
при
является точкой строгого минимума, а
при
![]() - точкой строгого максимума функции
.
- точкой строгого максимума функции
.
Отметим также, что точка, в которой функция определена, а ее производная равна нулю, называется стационарной точкой, а точка, в которой функция определена, а ее производная либо равна нулю, либо не существует, называется критической точкой.
В заключении этого пункта запишем правило нахождения тех значений , при которых достигает максимума или минимума:
• нужно найти ;
• найти
те значения
,
при которых
обращается в нуль или не существует,
т.е. решить уравнение
![]() и определить точки разравы функции
;
и определить точки разравы функции
;
• исследовать изменение знака при переходе через эти значения по следующей схеме
Таблица 5.
|
|
|
|
|
|
|
|
|
|
максимум |
|
Таблица 6.
|
|
|
|
|
|
|
|
|
|
минимум |
|
Значения , в которых исследуется знак производной, нужно брать достаточно близкими к . Стрелка означает, что в рассатриваемом промежутке функция убывает, стрелка обозначает возрастание функции. Если производная сохраняет знак при переходе через , то экстремума в точке нет.
Пример 15. Найти максимумы и минимумы функции
![]()
Решение. Функция определена и дифференцируема на всей числовой оси. Найдем первую производную
![]()
![]()
Производная
определена на всей числовой оси. Очевидно,
что
равна нулю в точках
![]()
![]() ,
,
![]() .
.
Исследуем
знак
в зависимости от расположения точки
на числовой оси. Заметим, что в выражении
![]() множитель
множитель
![]() неотрицателен для всех
,
поэтому на знак
влияют только множители
неотрицателен для всех
,
поэтому на знак
влияют только множители
![]() и
и
![]() .
При
.
При
![]() выражение
меньше нуля и
выражение
меньше нуля и
![]() (чтобы в этом убедиться, достаточно
положить
равным нулю). Когда
(чтобы в этом убедиться, достаточно
положить
равным нулю). Когда
![]() получим
получим
![]() и
.
При
и
.
При
![]() будем иметь
и
будем иметь
и
![]() .
Наконец, при
.
Наконец, при
![]() получим
и
.
Сведем полученные результаты в таблицу:
получим
и
.
Сведем полученные результаты в таблицу:
Таблица 7.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
макс. |
|
|
|
|
|
Итак,
![]() являетя точком максимума и значения
функции
в этой точке равно
.
Точка
- точка минимума, при этом
являетя точком максимума и значения
функции
в этой точке равно
.
Точка
- точка минимума, при этом
![]() .
.
График
функции
![]() изображен на рис. 34.
изображен на рис. 34.
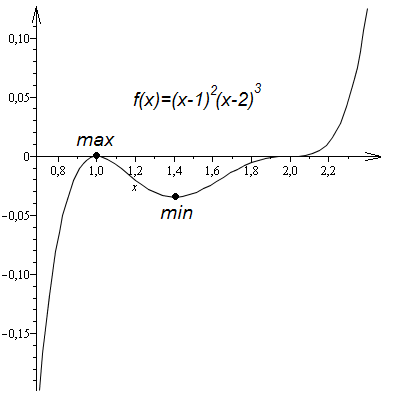
Рис.
34. График функции
при
![]() .
.
