3. Построение графиков функций, не являющихся элементарными

Определение функции не предполагает, что функция обязательно задается одной формулой. Может оказаться так, что на различных участках изменения аргумента функция задаетя различными аналитическими выражениями. Приведем некоторые примеры.

Пример 4. Поcтроить график функции сигнум, которая задается выражением

Решение. Если , то функция задана равенством и ее графиком будет полупрямая, параллельная оси , причем точка не будет принадлежать графику сигнума (будет выколотой). Для значений функция и ее графиком будет полупрямая, параллельная оси , причем точка будет выколотой. При сигнум тоже равен нулю, поэтому на графике следует изобразить точку . Таким образом, сигнум является кусочно-постоянной функцией. Его график изображен на рис. 14.

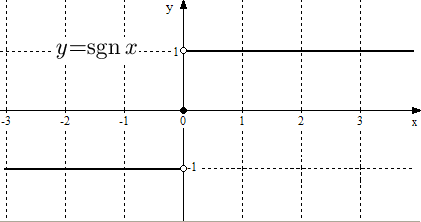
Рис. 14. График функции .

Пример 5. Пусть , где обозначает наибольшее целое чило, не превосходящее . Функция называется целой чаcтью числа . Построить график .

Решение. Если - целое число, то . Если , то , если , то и т.д. Рассмотрим отрицательные значения . Если , то , если , то и т.д. График функции показан на рис. 15. Отметим, что левые концы сплошных отрезков принадлежат графику, а правые - не принадлежат.

Пример 6. Построить график функции . Функция называется дробной частью числа .

Решение. Дробная часть числа удовлетворяет неравенствам . Если целое, то, очевидно, его дробная часть равна нулю: . При получим , при имеем , при получим и т.д. Если , то . Если , то и т.д. График функции изображен на рис. 16. Заметим, что левые концы сплошных отрезков принадлежат графику, а правые - не принадлежат.

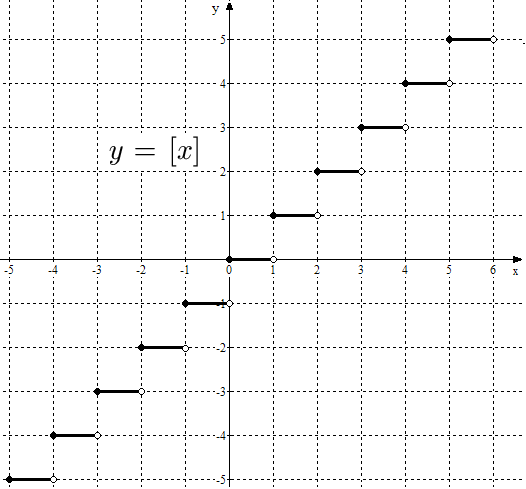
Рис. 15. График функции .

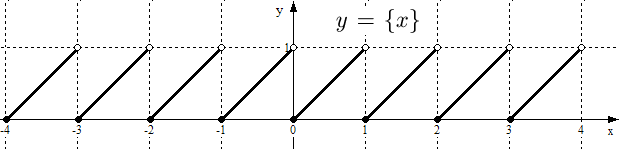
Рис. 16. График функции .

Пример 7. Построить график функции, определенной равенством

Решение. Функция задает прямую, проходящую через точки и . Изобразим эту прямую при . Функция - это парабола, ветви которой направлены вниз. Её вершина находится в точке (0,1). Парабола проходит через точки и . Наконец, при , изобразим прямую , проходящую через точки и . Получим график непрерывной функции (см. рис. 17).

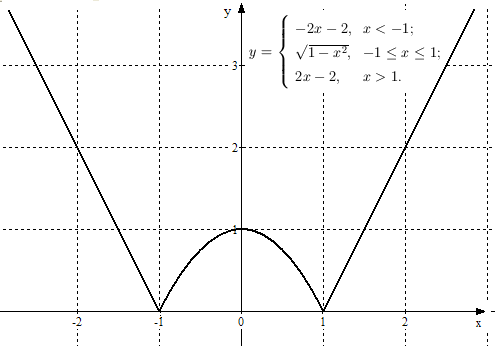
Рис. 17. К примеру 7.

4. Действия с графиками функций

В этом пункте мы рассмотрим сложение, вычитание, умножение и деление графиков функций. Также по графикам двух известных функций построим график суперпозиции этих функций.

4.1. Сложение и вычитание графиков

Сложение. Пусть даны две функции и и их графики изветны. Требуется изобразить график функции . Для этого построим на одном чертеже графики слагаемых функций. Затем проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны сумме ординат слагаемых функций. Например (см. рис. 18), при имеем , , значит . Заметим, что при сложении нужно учитывать знак ординат, например, при имеем , а , значит .

Соединяя полученные точки плавной кривой, получим эскиз графика функции (см. рис. 18).

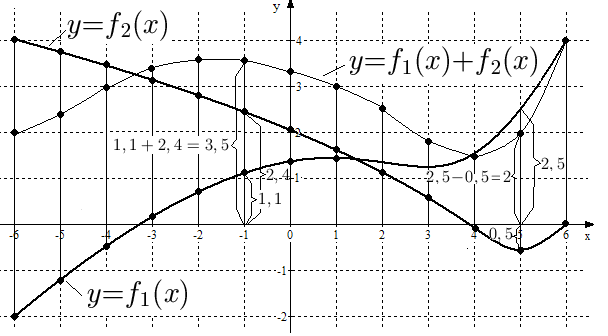
Рис. 18. Графики функций , и .

Вычитание. При построении эскиза графика разности двух функций , графики которых известны можно либо сложить графики функций и либо провести вертикальные прямые, пересекающих графики функций и , и отметить на них точки, ординаты которых равны разности ординат функций и .

Пример 8. Построить график функции .

Решение. График функции есть прямая, проходящая через точки и , график изображен на рис. 7. Построим график функции сложением графиков функций и (см. рис. 19).

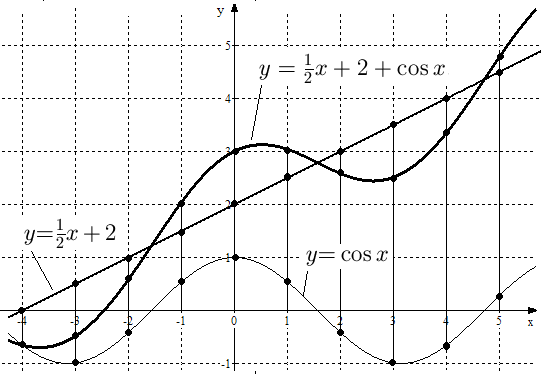
Рис. 19. Графики функций , и .

Пример 9. Построить график функции .

Решение. Построим графики функций и и вычтем график второй функции из графика первой (см. рис. 20). При этом, учитывая вид графика вертикальные прямые, пересекающие графики функций, будем проводить на расстоянии друг от друга.

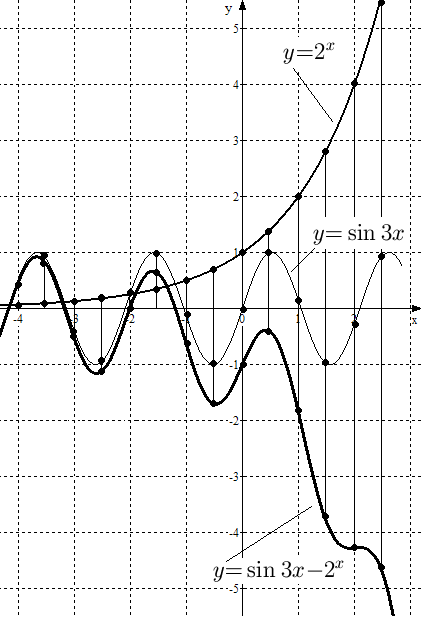
Рис. 20. Графики функций , и .