4.2. Умножение и деление графиков

Изучим правила перемножения и деления графиков функций. Рассмотрим как построить график суперпозиции двух функций. Приведем некоторые примеры.

Произведение. Пусть известны графики двух функций и . Построим график функции . Для этого изобразим на одном чертеже графики функций, входящих в произведение. Затем проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны произведению ординат перемножаемых функций. При этом, если ордината одной их функций, входящих в произведение равна нулю, т.е. ее график пересекает ось , то и ордината произведения будет равна нулю, т.е. график будет пересекать ось при том же значении абсциссы. Если ордината одной их функций или равна , то ордината произведения этих функций будет раположена на графике другой функции. Если перемножаются ординаты одного знака (либо обе ординаты имеют знак " ", либо обе ординаты имеют знак " "), то произведение будет положительно. Если в произведение входят ординаты разных знаков (одна ордината имеет знак " ", а другая " "), то их произведение будет отрицательно. Соединяя полученные точки плавной кривой, получим эскиз графика функции (см. рис. ).

Например (см. рис. 21), при имеем , , значит .

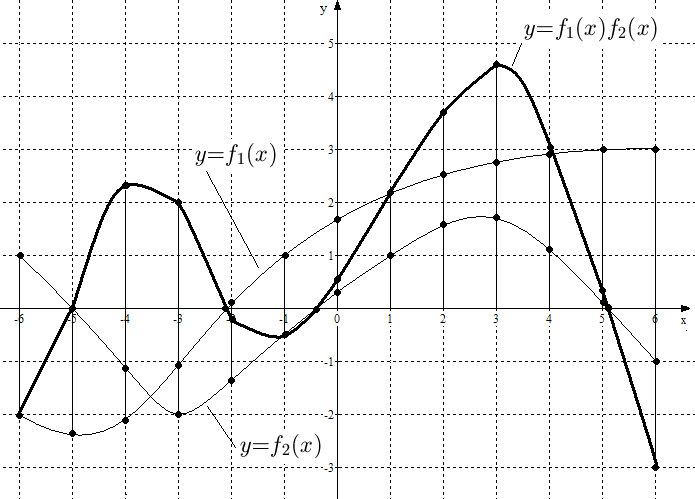
Рис. 21. Графики функций , и .

Пример 10. Построить график функции .

Решение. График функций и нам известны. График - бисектрисса первого и третьего координатных углов, а график изображен на рис. 22. Заметим, что функция - нечётная и - нечётная, поэтому их произведение - чётная функция. Следовательно, достаточно построить график только для , а затем симметрично отобразить на полуплоскость . Заметим также, что поскольку , то произведение , т.е. график не выходит за пределы линий и .

Итак, пусть . В точках , где произведение равно нулю, следовательно в этих точках график пересекает ось . Удобно также отметить точки, в которых , поскольку при график попадает на прямую , а при - на прямую .

Проведя вертикальные прямые через точки , ..., и перемножая соответствующие ординаты функций и , получим график функции (см. рис. 22).

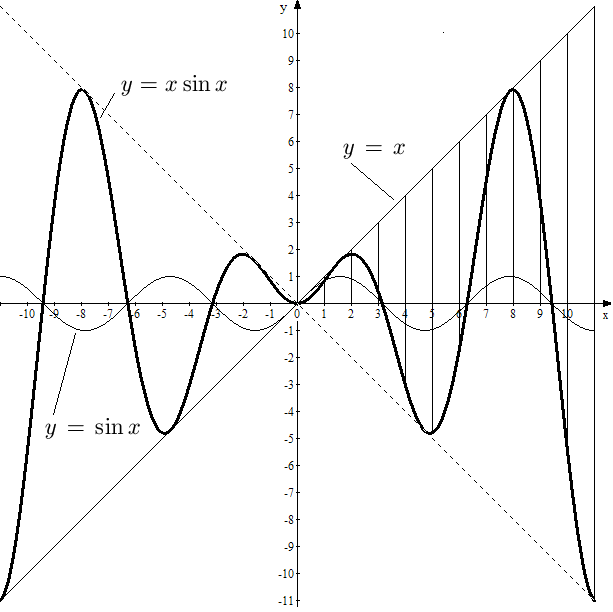
Рис. 22. Графики функций , и .

Частное. Теперь, зная графики функций и изобразим график функции . Если знаменатель дроби отличен от нуля: , то при делении графиков совершаются действия, аналогичные действиям при умножении графиков. А именно, изображаются графики и , проводится ряд вертикальных прямых, пересекающих эти графики, отмечаются точки, ординаты которых равны , полученные точки соединяются плавной линией (см. рис. 23).

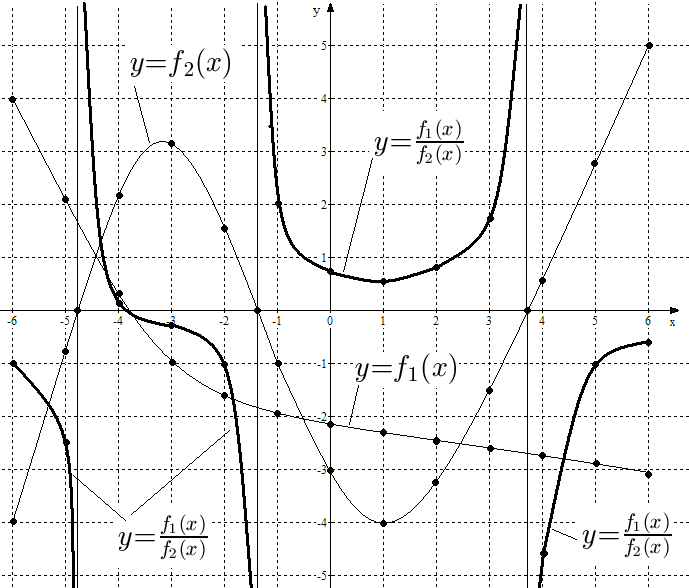
Рис. 23. Графики функций , и .

Точки, в которых заслуживают особого внимания, поскольку в этих точках функция не существует. В окрестнотях точек, в которых знаменатель функция может вести себя по разному. Рассмотрим возможные варианты.

Пусть при ( ). Возможны два случая: или .

При функция неограниченно возрастает или убывает в окрестности точки . В этом случае, нужно обратить внимание на знак частного при и при . Рассмотрим, например, правую окрестность, т.е. точки , которые больше : . Если при , достаточно близких к , таких, что частное , то график функции будет уходить вверх, прижимаясь справа к прямой , но не пересекая её. Если же , то график будет идти вниз, прижимаясь справа к прямой (см. рис. 23).

Аналогично поведет себя график и в левой окрестности, т.е. при (только прижиматься к прямой график будет слева) (см. рис. 23).

Ситуацию когда и и можно тщательно изучить только пользуясь теорией пределов, однако в некоторых случаях можно определить поведение функции исходя из графиков и и в этом случае.

Отметим также, что для построения частного можно перемножить графики и .

Замечание. При построении графиков произведения и частного двух функций полезно помнить, что если обе функции и чётные или обе нечётные, то и произведение и частное будет чётной функцией. Если же одна из функций или нечётная, а другая чётная, то их произведение и частное будет нечётной функцией.

Пример 11. 3 Построить график функции .

Решение. Используя рис. 2 и таблицу 1 изобразим графики функций и (см. рис. 24).

Функции определена и непрерывна во всех точках, за исключением нуля.

Заметим, что - четная функция, причем при , функция тоже четная, причем для всех . Поэтому функция график будет симметричен относительно оси и расположен выше оси .

Построим график при . Проведем вертикальные линии, проходящие через точки , , , и отметим на них значение частного функций и . Так при будем иметь , при получим и т.д.

Замечая, что при знаменатель дроби обращаетя в нуль, а числитель отличен от нуля (равен единице), и учитывая, что для всех (значит, и в любой окрестности точки ) получим, что график рассматриваемой функции при будет уходить вверх, прижимаясь справа к оси .

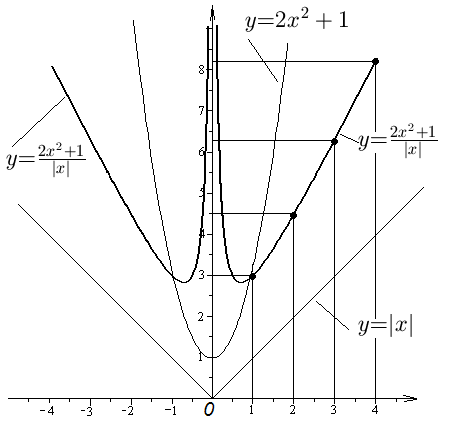
Рис. 24. Графики функций , и .

Соединяя отмеченные точки и рисуя график функции в промежетке от до уходящим вверх и приближающимся справа к оси , получим график функции при . В силу четности рассматриваемой функции, слева от оси изображаем кривую, симметричную кривой справа от оси , получаем искомый график (см. рис. 24).