1.3. Тригонометрические функции

Тригонометрические функции и опредены на всей числовой оси, переодические, с периодом и не принимают значения по абсолютной величине большие . Отметим также, что функция является нечетной, а функция - четной. Их графики изображены на рис. 7.

Линия, являющаяся графиком функции , называется синусоидой. График функции - тоже синусоида, она получается из графика смещением вдоль влево на отрезок .

Из рис. 7 видно, что график функции проходит через точку - начало координат, а функция проходит через точку . Графики обеих функций и и пересекают ось неограниченное число раз, это означает, что уравнения и имеют бесконечно много корней. Именно, решение уравнения имеет вид , где - целое число, а решением уравнения будут число , где - целое число.

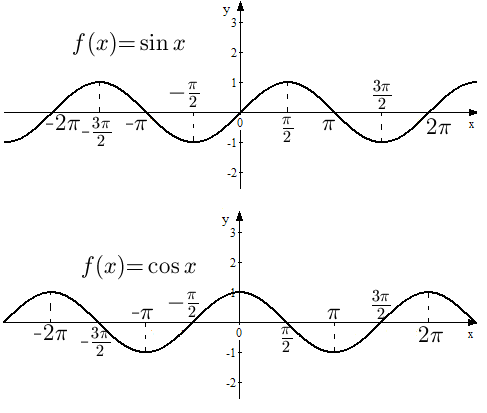
Рис. 7. Графики функции и .

Тангенс и котангенс выражаются формулами и , а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у в знаменателе находится , который обращается в нуль в точках , а будет иметь разрывы там, где синус равен нулю, т.е. в точках ( - целое число).

Обе функции и и являются нечетными и периодическими с периодом . Графики этих функций приведены на рис. 8.

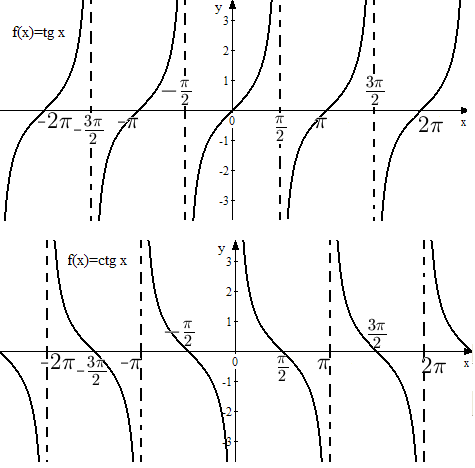
Рис. 8. Графики функции и .

1.4. Обратные тригонометрические функции

Обратные тригонометрические функции ставят в соответствие значению данной тригонометрической функции значение угла. Так, например, есть угол, синус которого равен . Аналогично определяются , и .

Полагаем

(1)

(2)

Справедливы следующие формулы сложения обратных тригонометрических функций

Графики обратных тригонометрических функций изображены на рис. 9.

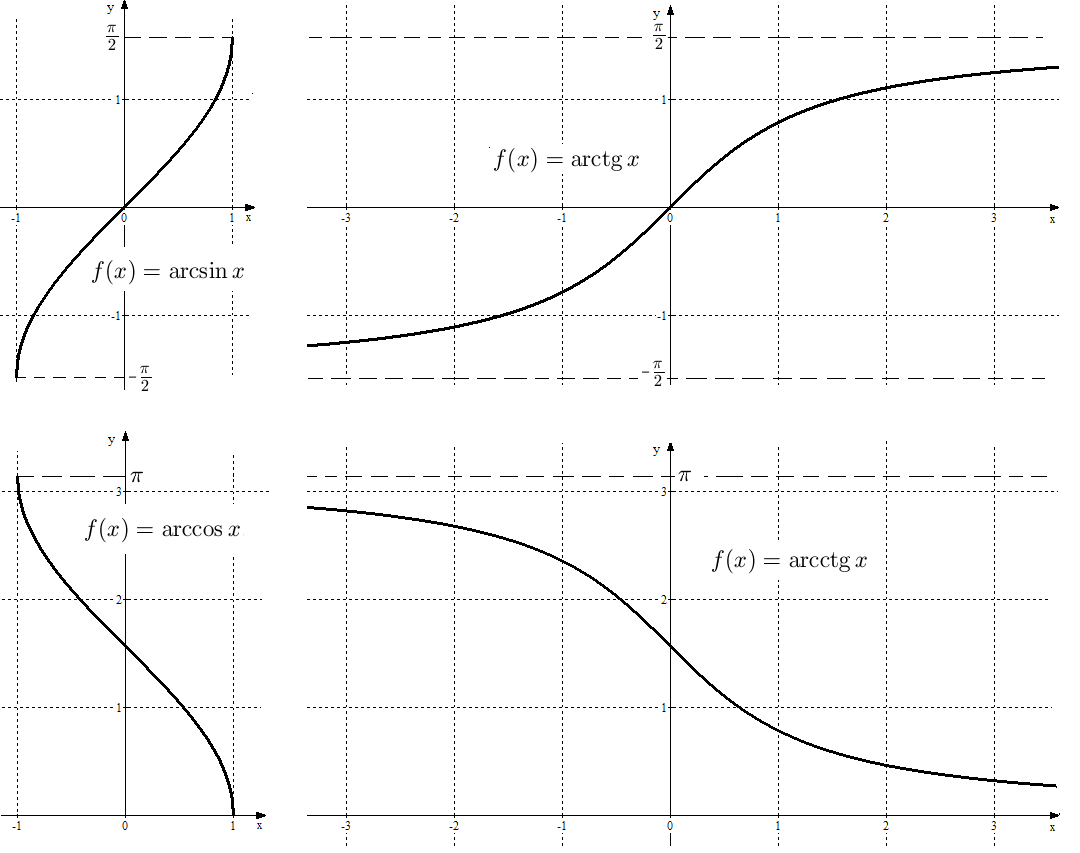
Рис. 9. Графики функций , , и .

2. Элементарные преобразования графиков

Допустим, что построен график функции , . Тогда построение графика в общем случае сводится к ряду элементарных преобразований, таких как сдвиг, сжатие, отображение и т.д. графика функции .

Приведем таблицу, в которой описано, как изменяется график функции приопределенном преобразовании функции или ее аргумента (см. таблицу 1).

Таблица 1

№	Функция	Преобразование, которое следует провести с графиком на плоскости
1.	,	Сдвиг вверх по оси графика функции на единиц, если , и сдвиг вниз на единиц, если .
2.	,	Сдвиг вправо по оси на единиц, если , сдвиг влево на единиц, если .
3.	, ,	Растяжение вдоль оси относительно в раз, если , сжатие вдоль оси в раз, если .
4.	, ,	Сжатие вдоль оси относительно в раз, если , растяжение вдоль оси в раз, если .
5.		Симметричное отображение графика относительно оси .
6.		Часть графика, расположенная ниже оси , симметрично отражается относительно этой оси, остальная часть остается без изменения.
7.		Симметричное отображение графика относительно оси .
8.		Стирается часть графика функции , лежащая слева от оси , остается часть графика , лежащая справа от оси и на ней; часть графика, расположенная в области , симметрично отображается относительно оси в область .

Для того, чтобы на практике построить график функции , используя график и элементарные преобразования графика следует использовать такой порядок:

• построить график ;

• построить график функции , для этого сжать или растянуть график вдоль оси и, если, симметрично отобразить относительно ;

• сдвинуть по оси полученный график, так, чтобы получился график функции ;

• построить график функции , для этого сжать или растянуть график вдоль оси и, если , симметрично отобразить относительно оси ;

• сдвинуть график на вверх, если , и вниз на , если .

Пример 1. Построить график функции .

Решение. Сначала преобразуем функцию, вынеся за скобки коэффициент при : . Теперь последовательно выполним преобразования графика функции , который изображен на рис. 7 (см. также рис. 10).

Построим график . Так как больше единицы, то график нужно сжать вдоль в раза (см. преобразование 4 из таблицы 1). Получим

Рис. 10. Графики функций , .

Сдвинем теперь по оси полученный график на вправо (см. преобразование 2 из таблицы 1), получим график функции (см. рис. 11). Наконец, растянем график в раза вдоль (см. преобразование 3 из таблицы 1), чтобы получить требуемый график (см. рис. 11).

Пример 2. Поcтроить график функции

Решение. Построем сначала , затем растянем его вдоль оси в два раза, получим график . Чтобы теперь получить эскиз ту часть графика, которая находится выше оси симметрично отобразим в нижнюю полуплоскость, оставив без изменения часть графика , которая лежит ниже оси (см. рис. 12).

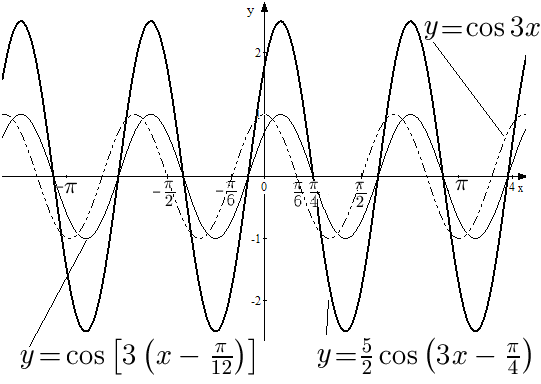
Рис. 11. Графики функций , и .

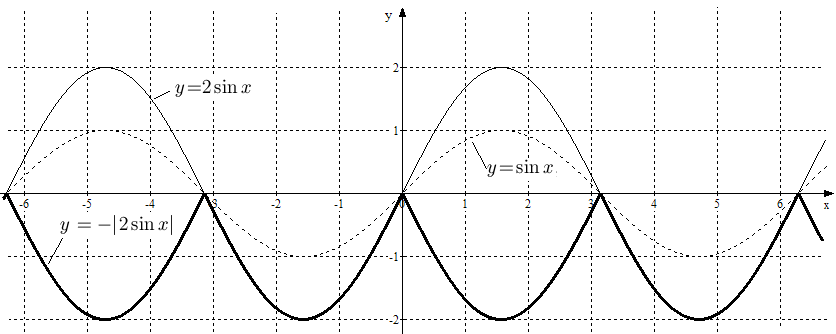
Рис. 12. Графики функций , и .

Пример 3. Построить график функции .

Решение. Построение эскиза графика функции сводится к следующему (см. рис. 13):

1. строится график ;

2. построенный график сжимается вдоль оси в два раза, получается график ;

3. график симметрично отображается относительно оси , получается график ;

4. наконец, график сдвигается вниз на .

Рис. 13. Графики функций , , и .