6. Построение графика функции, заданной параметрически

Пусть имеем две функции и , где - общей для и области определения. Вычисляя при и считаем, что полученное значение есть функция от полученного . Тем самым получаем функцию . Такое приведение, параметрически заданной, функции к явной не всегда возможно и может быть потеряна часть информации. Параметрически заданную функцию удобно тракторвать как уравнение движения точки на плоскости. В момент времени мы знаем координаты точки . Множество всех точек , где , называетя графиком функции или траекторией движения точки. При построении графика получаем направление движения точки.

Основной метод построения графика функции, заданной параметрически, состоит в том, чтобы разбить весь график на монотонные и непрерывные куски (ветви). Монотонную и непрерывную ветвь можно строить по точкам, используя при этом исследование функции на концах промежутка, если на концах хотя бы одна из функций или разрывна.

6.1. Порядок построения графика параметрически заданной функции

• Найти - область определения по общую для и и отметить её на числовой оси , там же отметить точки разрыва функций.

• Найти производные и и их область определения и отметить её на той же числовой оси , также отметить точки разрыва производных.

• Решить уравнения , и нули производных отметить на той же оси.

Тем самым ось будет разбита на промежутки, на каждом из которых , и вместе с ними будут монотонны и непрерывны.

Результат исследования на монотонность функций и оформляют в виде таблицы (см. ниже в решении примера). По таблице строится черновик графика, который позже уточняется нахождением асимптот, участков выпуклости определённого знака и точек перегиба.

6. 2. Асимптоты параметрического графика

• Если при некотором или и , то - горизонтальная асимптота. Пределы слева и справа вычисляются отдельно, т.к. это могут быть две разные асимптоты. Эти пределы уже бывают вычислены при заполнении таблицы.

• Если , или , то -вертикальная асимптота.

• Если или и или , то возможно, у этой ветви есть наклонная асимптота , где

Если существует, то ищем :

Если - существует, то у соответствующей ветви будет наклонная асимптота .

6. 3. Точки перегиба

Для нахождения участков выпуклости и точек перегиба нужна производная , которая находится по формуле

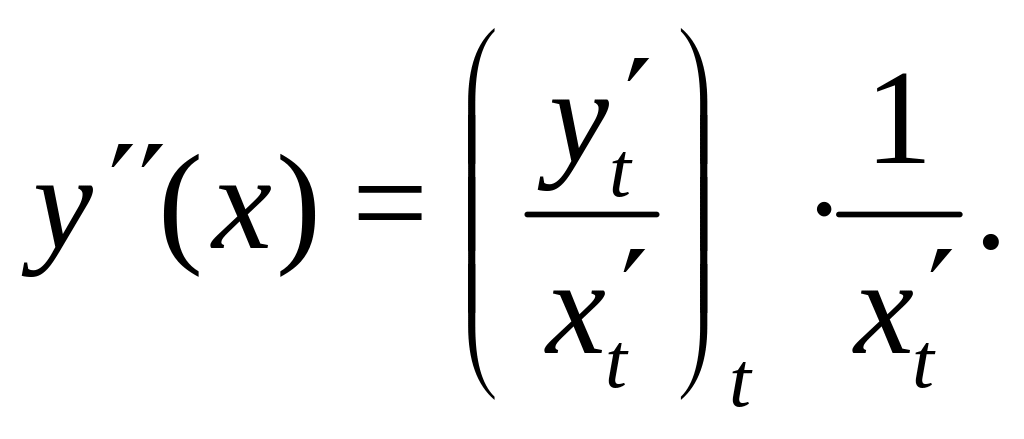
Исследуем знак , определяем направдение выпуклости, находим точки перегиба, если есть, и корректируем черновик графика.

6.4. Пример построения графика параметрически заданной функции

Пример 18. 21 Построить эскиз графика , .

Решение. Совокупная область определения: .

Найдем , :

Получаем, что не существует при , при , не существует при и в нуль не обращается.

На ось наносим точки , , (см. рис. 40):

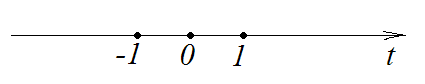
Рис. 40. Ось .

Мы получили четыре интервала. На каждом интервале функции , , а вместе с ними и будут непрерывны и монотонны. Осталось найти промежутки изменения функций и . Другими словами, откуда и куда движется точка по плоскости. Результат такого иследования оформляем в виде таблицы. Основных трок в таблице четыре, а столбцов только, сколько отмечено интервалов на оси .

Таблица 14.

Знак
	Убывает	Убывает	Возрастает	Возрастает
	от до	от до	от до	от до
Знак
	Возрастает	Возрастает	Возрастает	Убывает
	от до	от до	от до	от до

Для заполнения первой клетки изменения функции вычисляем

Для первой клетки функции вычисляем

Аналогично заполняются остальные клетки. В точках непрерывности вычисляем просто значение функции.

Для построения графика читаем таблицу по столбцам. Получаем, что переменная точка движется от точки неограниченно влнво ( - убывает) и одновременно поднимается от до .

В данном случае при имеем горизонтальную асимптоту . Получим монотонную ветвь по которой точка движется влево (см. рис. 41). Правый конец ветви на рис. 41 соответствует , левый - .

Рис. 41. Ветвь графика функции , при .

Остальные три ветви строим аналогично как движение точки в нужном направлении.

Для уточнения графика на ветви найдем хотя бы одну точку. Выберем получим округлённо . На ветви возьмем получим .

Исследуем направление выпуклости. Находим

Наносим на ось точки разрыва функций , и нули . Находим и проставляем знаки . (см. рис. 42).

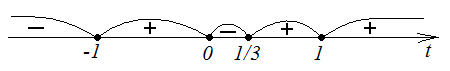
Рис. 42. Ось и знаки .

При получаем точку перегиба .

При кривая будет выпукла вверх, при - выпукла вниз, при - выпукла вверх, при - выпукла вниз, при - выпукла вниз.

При имеем , , поэтому у ветви может быть наклонная асимптота. Проверим это:

Это значит, что асимптоты не существует. У ветви при проверка показывает отсутствие аимптоты. При - горизонтальная асимптота . Заметим также, что при любых , поэтому график функции находится выше оси .

График функции , изображен на рис. 43.

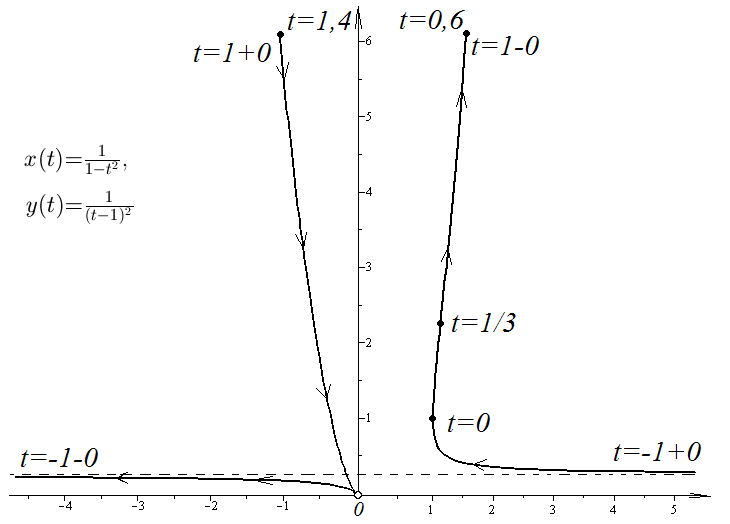
Рис. 43. График функции , .