4. Асимптоты

Использование понятия предела часто позволяет более точно отразить свойства функции при построении ее графика. Так нахождение наклонной и вертикальной асимптот основывается на вычислении предела.

Асимптота может быть определена как прямая, расстояние до которой от графика функции стремится к нулю, когда точка «стремится, оставаясь на графике, в бесконечность» (при ). (см. рис. 38).

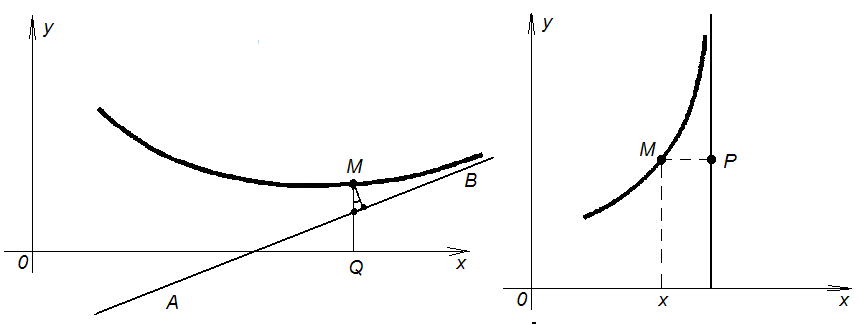
Рис. 38. Наклонная и вертикальная асимптоты.

Дадим точное определение наклонной асимптоты.

Определение 8. 19 Пусть функция определена для всех (соответственно для всех ). Если существуют такие числа и , что

(соответственно при ), то прямая

называется наклонной асимптотой графика функции при (соответственно при ).

Числа и находятся по формулам

и

Заметим, что при таком определении мы ни при каких значениях и не можем получить прямую, параллельную оси , поэтому приведем еще одно определение - определение вертикальной асимптоты.

Определение 9. 20 Пусть функция определена в некоторой окрестности точки (быть может, односторонней) и пусть выполнено хотя бы одно из условий , или , тогда прямая называется вертикальной асимптотой графика функции .

5. Порядок построения графика функции, заданной выражением

Приведем схему действий, которые нужно проделать для построения графика функции .

Нужно

• найти область определения функции и исследовать поведение функции в граничных точках области определения;

• исследовать функцию на симметрию графика и периодичность;

• найти точки разрыва функции и промежутки непрерывности;

• определить точки пересечения графика функции с координатными осями и области постоянства знака функции;

• найти асимптоты;

• найти точки экстремума и промежутки возрастания и убывания функции;

• определить точки перегиба и установить промежутки вогнутости вверх (вниз);

• построить график функции.

Пример 17. Построить график функции .

Решение. Проведем полное исследование функции.

1. Найдем область определения этой функции. Функция существует при всех значениях , кроме , при котором знаменатель обращается в нуль. Следовательно, область определения функции

2. Исследуем вопрос о симметрии графика, т.е. проверим является ли данная функция четной, нечетной или функцией общего вида. Для этого выясним, выполняется ли одно из равенств или :

Ни одно из проверяемых равенств не выполняется, так что функция не является ни четной ни нечетной.

Очевидно, функция не является переоидической.

3. Числитель и знаменатель дроби непрерывные функции, поэтому функция будет непрерывной при всех значениях , кроме , при котором знаменатель дроби обращается в нуль.

4. Определим точки пересечения графика функции с осями координат. График пересекает ось при :

Для нахождения точек пересечения графика с осью решим уравнение

Оно имеет единственное решение: . Таким образом, точки пересечения с координатными осями: и .

Найдем области постоянства знака функции, т.е. промежутки где функция положительна и отрицательна. Поскольку график пересекает ось в точке , а также поскольку функция может принимать значения разных знаков по разные стороны от точки разрава, то нужно исследовать какой знак имеет функция при , и при . Очевидно, при и при . Таким образом,

Таблица 11.

x		-1	(-1,1)	1
f(x)		не сущ.		0	+

5. Определим асимптоты.

а) Вертикальные асимптоты найдем, приравняв знаменатель к нулю: ; . Следовательно, вертикальная асимптота одна: ее уравнение .

б) Наклонные асимптоты:

Аналогично

Это означает, что наклонная асимптота одна:

6. Найдем точки экстремума и промежутки возрастания и убывания функции. Первая производная имеет вид

Определим критические точки.

1) Решая уравнение , находим , .

2) Значением при котором не существует является . Эта точка не входит в область определения функции, поэтому не будет являтся экстремальной.

Определим знак производной функции в каждом из интервалов :

Таблица 12.

				не сущ.
				не сущ.

При функция имеет максимум и . Поскольку знаки во втором и третьем интервалах различны, то можно было бы предположить, что при есть экстремум. Однако, такое предположение неверно, так как при заданная функция не существует. Таким образом, функция имеет единственный экстремум при . Координаты точки максимума .

7. Определим интервалы выпуклости и вогнутости графика функции и точки перегиба.

Найдем, что

и определим критические точки второго рода.

1) Решая уравнение , найдем что .

2) При вторая производная функции не существует.

Исследуем поведение второй производной на интервалах , , :

Таблица 13.

		не сущ.
		не сущ.

Значит, в интервалах и кривая выпукла вверх, а в интервале - выпукла вниз. При переходе через точку вторая производная поменяла знак и это означает что при кривая имеет точку перегиба. Координаты точки перегиба .

8. Используя сведения, полученные в пунктах 1-7 построим график функции (см. рис. 39).

Рис. 39. График функции .