§5. Приложения степенных рядов к приближенным вычислениям
5.1. Приближенное вычисление логарифмов.
Для приближенного вычисления логарифмов удобно использовать формулу
где N – натуральное число. Эта формула позволяет последовательно найти логарифмы целых чисел, причем сходимость ряда тем быстрее, чем больше N.
5.2. Приближенное вычисление корней.
Приближенное вычисление корней производится с помощью биноминального ряда
5.3. Приближенное вычисление определенных интегралов.
Многие нужные определенные интегралы не вычисляются с помощью формулы Ньютона-Лейбница, так как ее применение связано с поиском первообразной, часто не выражаемой в элементарных функциях. Однако, если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то приближенное вычисление интеграла оказывается осуществимым с наперед заданной точностью.
II. Пример выполнения контрольной работы.
Задание 591-600.
Пример 1.
Исследовать на сходимость, с помощью необходимого признака, ряды:
а)
б)
Решение.
а)
Необходимое условие сходимости ряда выполняется, но о сходимости ряда ничего нельзя сказать (как будет видно из дальнейшего, ряд расходится).
б)
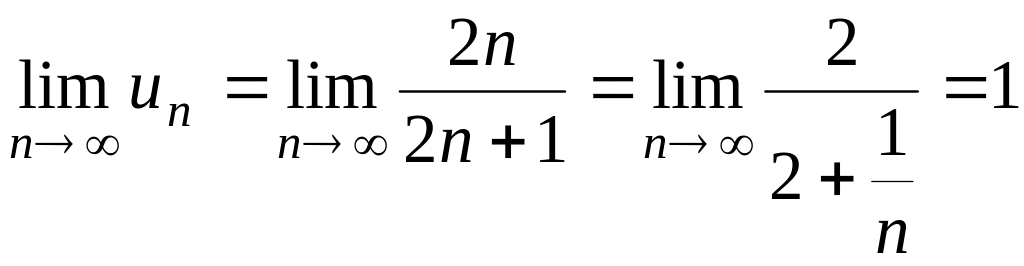
Необходимое условие сходимости ряда не выполняется и, следовательно, этот ряд расходится.
Пример 2.
Исследовать на сходимость, используя признак сравнения, ряды:
а)
б)
Решение.
а) Общий член данного ряда
,
так как с увеличением
знаменателя дробь уменьшается; но ряд
– гармонический, расходящийся,
следовательно, данный ряд расходится
и подавно.
б) Общий член
данного ряда
меньше общего члена сходящегося ряда
геометрической прогрессии
,
поэтому данный ряд сходится.
Пример 3.
Исследовать на
сходимость, используя предельную форму
признака сравнения, ряд
.
Решение.
Известно, что
,
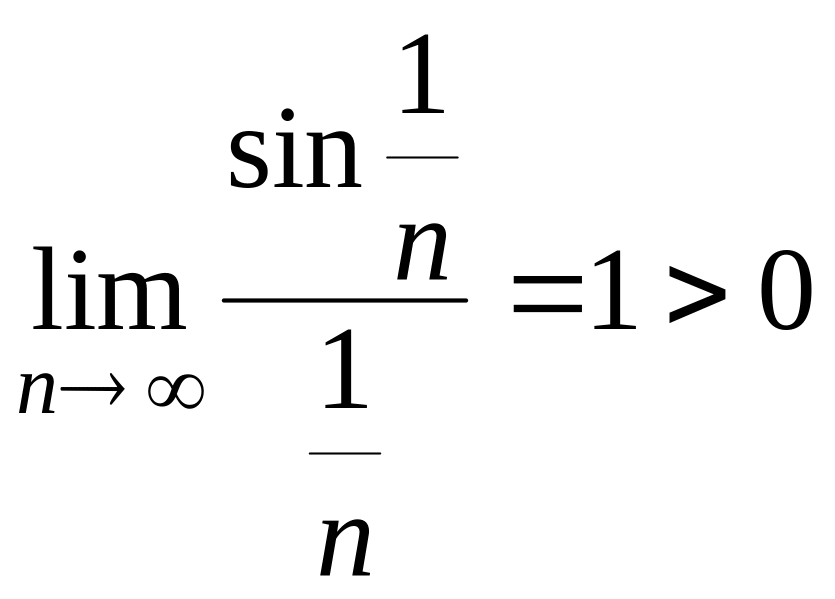но гармонический ряд
расходится, следовательно, и данный ряд
расходится.
Пример 4.
Исследовать на сходимость ряд .
Решение.
Степень многочлена в числителе равна k =1, степень знаменателя l=2. Сравним данный ряд с гармоническим рядом:
;
заключаем, что данный ряд расходится.
Пример 5.
Исследовать на
сходимость ряд
,
пользуясь признаком Коши.
Решение.
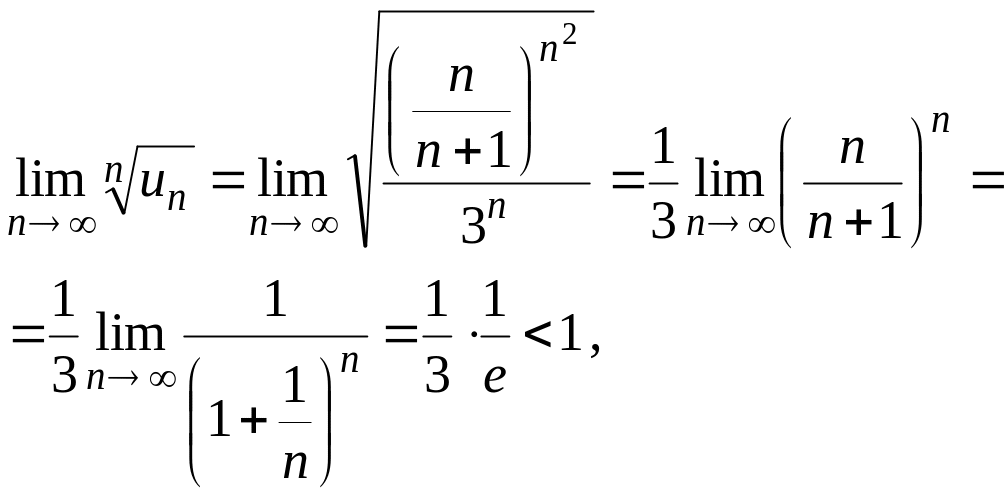
следовательно, ряд сходится.
Пример 6.
Исследовать на
сходимость ряд
,
пользуясь признаком Даламбера.
Решение.
;
,
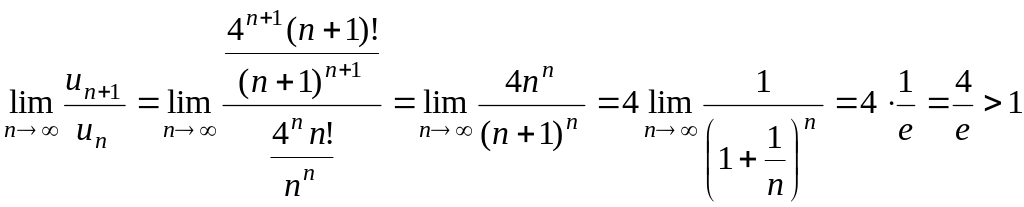(e=2,71…),
следовательно, по признаку Даламбера, ряд расходится.
Пример 7.
Исследовать на
сходимость ряд
,
пользуясь интегральным признаком.
Решение.
Для применения
интегрального признака нужно рассматривать
несобственный интеграл
.
Значение a
выберем позже, после получения
первообразной.
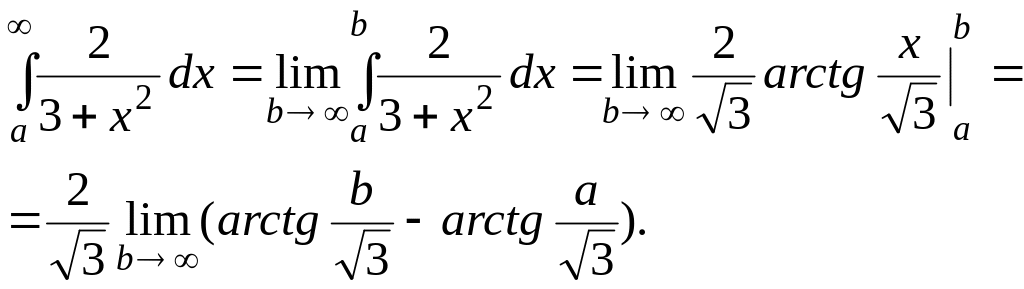
Выберем a=0
(
0
не равен ∞), тогда
Так как несобственный
интеграл существует и равен конечной
величине, следовательно, он сходится,
а значит, сходится и ряд
.
Задание 601-610.
Пример 8.
Исследовать на
сходимость и абсолютную сходимость ряд
.
Найти приближенно (с точностью 0,01) сумму
этого ряда.
Решение.
Ряд знакочередующийся,
,
члены ряда по модулю монотонно убывают.
Следовательно, этот ряд сходится. Более
того, этот ряд сходится абсолютно, так
как сходится ряд из абсолютных величин
членов данного ряда
Сходимость этого
ряда легко установить, если применить
предельный признак сравнения со
сходящимся рядом
:
.
Для того, чтобы
найти сумму данного ряда с точностью
0,01, надо взять столько его членов, чтобы
следующий член ряда был по модулю меньше
0,01. Тогда весь остаток ряда, начинающийся
с этого члена, будет также меньше 0,01.
Для данного ряда модуль четвертого
члена
,
поэтому с точностью 0,01:
