18

Государственное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Высшая математика»

Лапшина Н.В., Соловьёва И.М., Спиридонов Е.И., Шварц М.А.

Кратные и криволинейные интегралы Контрольная работа № 6

Методические указания и контрольные задания

для студентов заочного факультета

Санкт-петербург

2005

В соответствии с рабочей программой в контрольную работу № 6 включены следующие темы:

1. Комплексные числа, их изображения на плоскости. Алгебраическая, тригонометрическая и показательная форма комплексного числа. Формулы Эйлера. Алгебраические действия над комплексными числами.

2. Геометрические приложения определенного интеграла (вычисление площадей плоских фигур).

3. Задачи, связанные с понятием двойного интеграла (изменение порядка интегрирования в повторных интегралах).

4. Механические приложения криволинейных интегралов (вычисление работы силы).

I. Вкратце остановимся на каждой из тем контрольной работы.

1. Комплексные числа

1.1. Алгебраическая форма комплексного числа. Действия над комплексными числами.

Комплексными называются числа вида , где и - действительные числа, а . Числа и называются соответственно действительной и мнимой частями комплексного числа . Они обозначаются , .

Два комплексных числа считаются равными, если равны отдельно их действительные и мнимые части. Число называется сопряженным числу .

Алгебраические действия над комплексными числами выполняются по формулам:

, (1)

, (2)

(3)

2. Геометрическое изображение комплексного числа.

Каждое комплексное число можно изобразить точкой плоскости , имеющей координаты , при этом точки оси изображают действительные числа, а оси - чисто мнимые. Можно также числу сопоставить вектор, направленный из начала координат О в точку (Рис.1). Длина r этого вектора, т.е. расстояние от точки до начала координат О, называется модулем комплексного числа и обозначается :

(4)

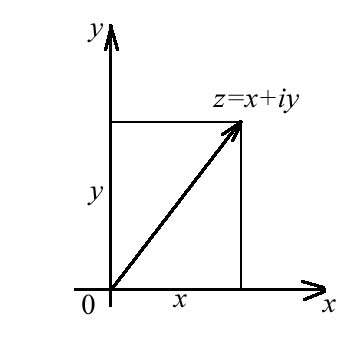
Рис.1

Угол , образованный вектором с положительным направлением оси , называется аргументом числа и обозначается Arg . Для аргумента справедливы формулы:

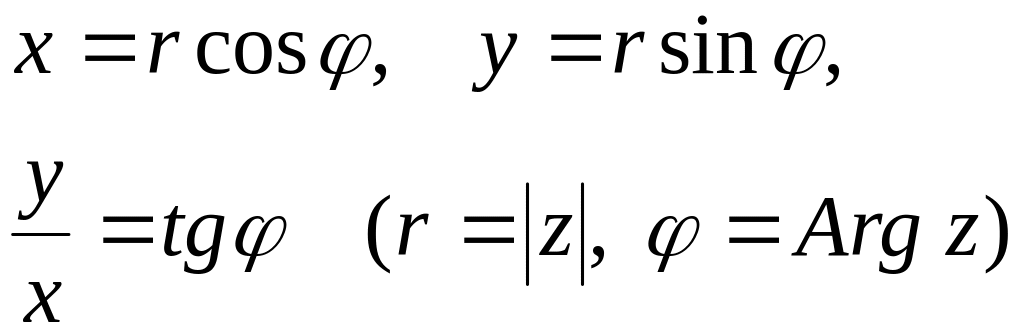(5)

Значения Arg определяются не однозначно, а с точностью до слагаемого

Фиксируя один период изменения в пределах < (или < ), выделяют главную ветвь аргумента, обозначаемую arg , так что Arg = arg +

2. Тригонометрическая и показательная формы комплексного числа.

Тригонометрическая форма комплексного числа имеет вид:

(6)

где r - модуль комплексного числа , а - главное значение его аргумента, причем .

Для возведения комплексных чисел в степень n удобна формула Муавра:

(7)

Корни степени n из комплексного числа определяются по формуле:

(8)

Показательная форма комплексного числа имеет вид: (9)