17

Государственное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Высшая математика»

Спиридонов Е.И.

Ряды Контрольная работа № 8

Методические указания и контрольные задания

для студентов заочного факультета

Санкт-петербург

2005

В соответствии с рабочей программой в контрольную работу № 8 включены следующие темы:

1. Числовые ряды. Сходимость ряда и его сумма. Необходимое условие сходимости.

Ряды с положительными членами. Признаки сравнения рядов. Признак Даламбера. Интегральный признак.

Знакопеременные ряды. Абсолютная и условная сходимости. Свойства абсолютно сходящихся рядов. Знакочередующиеся ряды. Признак Лейбница.

2. Функциональные ряды. Область сходимости. Равномерная сходимость функциональных рядов.

Степенные ряды. Интервал и радиус сходимости.

Разложение функций в ряд Тейлора. Ряд Маклорена для элементарных функций. Применение степенных рядов к приближенному интегрированию функций.

§1. Основные понятия

1. Определения.

Пусть дана бесконечная последовательность чисел

Числовым рядом называется составленное из этих чисел выражение

,

Числа называются членами ряда, – общим членом ряда.

Конечная сумма называется n-й частной суммой ряда.

Если существует конечный предел , ряд называется сходящимся, в противном случае – расходящимся. Если ряд сходится, число называется суммой ряда, а разность

называется остатком ряда (после n-го члена).

2. Необходимый признак сходимости.

Если ряд сходится, то его общий член стремится к нулю при . Отсюда следует, что если не стремится к нулю, то ряд расходится.

Указанный признак не является достаточным, т.е. если , то о сходимости ряда ничего еще сказать нельзя; он может быть как сходящимся, так и расходящимся.

§2. Признаки сходимости

1. Исследование на сходимость рядов с положительными членами.

1. Признак сравнения.

Если даны два ряда и с неотрицательными членами, причем члены первого ряда не превосходят соответствующих членов второго ряда:

,

то: а) из сходимости второго ряда следует сходимость первого ряда, б) из расходимости первого ряда следует расходимость второго ряда.

Для сравнения часто используются ряды:

1) , <1 – сходящийся (геометрическая прогрессия),

2)

(при – гармонический ряд)

2. Предельная форма признака сравнения.

Если и – ряды с положительными членами и существует конечный, отличный от нуля

,

то рассматриваемые ряды одновременно сходятся или расходятся.

3. Ряды вида .

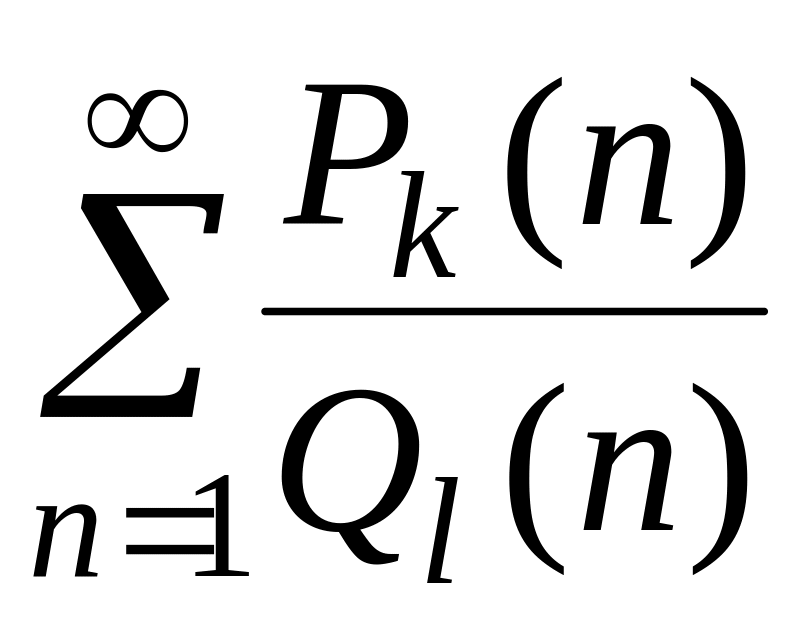Здесь – многочлен от n степени k, а – многочлен от n степени l. Вопрос о сходимости рядов такого вида полностью исчерпывается сравнением с рядом , где . Удобнее при этом использовать признак сравнения в предельной форме.

4. Признак Коши.

Если для ряда с положительными членами существует , то этот ряд сходится при l <1 и расходится, если l >1. Если l =1, то вопрос о поведении ряда остается открытым.

5. Признак Даламбера.

Если ряд с положительными членами таков, что существует , то при l <1 ряд сходится, а при l >1 ряд расходится. Если l =1, то вопрос о поведении ряда остается открытым.

6. Интегральный признак сходимости.

Если функция f(x) непрерывная, положительная, невозрастающая для и, начиная с некоторого N, , то ряд

и несобственный интеграл одновременно сходятся или расходятся. Рассматривая несобственный интеграл можно выбирать значение a любым, не обращающим первообразную F(x) в ∞.

2. Абсолютная сходимость. Теорема Лейбница о сходимости знакочередующихся рядов.

В этом пункте рассматриваются ряды с членами, имеющими любой знак.

Если ряд сходится, а ряд расходится, то ряд называют условно сходящимся. Если ряд сходится, то сходится и ряд , называемый в этом случае абсолютно сходящимся. Ряд

,

где все , называется знакочередующимся.

Теорема Лейбница.

Если все члены знакочередующегося ряда удовлетворяют условиям

и ,

то такой ряд сходится.

Ряд, удовлетворяющий указанным условиям, называется рядом Лейбница.

Остаток ряда Лейбница

имеет знак своего первого члена и меньше его по абсолютной величине, т.е. .

Это неравенство удобно использовать для оценки погрешности, получаемой при замене суммы S ряда Лейбница ее приближенным значением