§ 5 . Метод Ньютона.
Пусть требуется найти корень уравнения
(5.1)
Пусть х0 — начальное приближение. Разложим функцию в ряд тейлора в окрестности точки х0 :
где
—
некоторая точка из окрестности
.
Возьмем в этом разложении линейную
часть и запишем уравнение:
(5.2)
Это уравнение линейно. Обозначим его
решение через
.
Тогда
Теперь точку
считаем приближением к решению уравнения
(5.1) и проделываем с ней то же, что и с
.
Получаем
:
Продолжая этот процесс, построим
последовательность
по правилу:
, k = 1 , 2 , ...
(5.3)
Очевидно, чтобы последовательность
(5.3) можно было построить, функция
не должна обращаться в 0 ни в одной
из точек
.
Геометрический смысл этого построения.
Уравнение
является уравнением касательной к
кривой
в
точке
.
А решение уравнения (5.2) — точка пересечения
этой касательной с осью х .
Чтобы изучить вопрос о сходимости последовательности (5.3), перепишем уравнение (5.1) в виде:
(5.4)
Для этого уравнения можно построить
последовательные приближения по методу
итераций при
.
Легко показать, что
.
Действительно,
, т.к. х * — корень уравнения
(5.1). В то же время
,
следовательно, мы получили метод итераций
2-го порядка. Значит,
, где
—
ошибка, полученная на к -м шаге, а
—
некоторая точка в окрестности корня.
Таким
образом, ошибка на каждом следующем
шаге возводится в квадрат и если,
например,
, то сходимость к решению будет очень
быстрая. Иногда такую сходимость называют
квадратичной
Теперь рассмотрим метод Ньютона для систем уравнений. Пусть дана система нелинейных уравнений:
(5.5)
где
.
Пусть
— начальное приближение к решению
системы (5.5).
Замечание. Для систем вопрос о нахождении начального приближения очень сложный, и в общем виде не решается. Его удается решить только в некоторых простых частных случаях. Поэтому чаще всего начальное приближение дается вместе с задачей.
Разложим
в
ряд Тейлора, как вектор - функцию от
нескольких переменных в окрестности
точки
:
(5.6)
где
—
матрица Якоби. Она имеет вид:
(5.7)
Запишем линейную систему:
(5.8)
Эту систему можно считать приближенной к системе (5.5), поэтому ее решение можно считать приближением к решению системы (5.5). Поскольку система (5.8) линейная, мы можем найти ее решение:
Обозначим этот вектор через
.
Аналогично найдем
. Таким образом, мы построим последовательность
по
правилу:
(5.9)
Если эта последовательность сходится
к пределу
и все
ограничены, то
будет решением системы (5.5). (без
доказательства)
Если эта последовательность сходится к пределу и все ограничены, то будет решением системы (5.5). (без доказательства)
Рассмотрим систему 2-х уравнений:
Здесь
.
Тогда
.
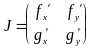Получим линейную систему
.
Решая эту систему, получаем приближения
по формулам:
где
Продолжая этот процесс, получаем общие формулы для построения приближенного решения:
,
k = 0
, 1 , 2 , ... (5.10)
где
