Лекция 1,2.
Литература.
И.П.Мысовских Лекции по методам вычислений . 1998.
Д.К.Фаддеев, В.Н.Фаддеева Вычислительные методы линейной алгебры. 2002.
И.С.Березин, Н.П.Жидков. Методы вычислений. Т. 1, 2. 1959.
В.И.Крылов, В.В.Бобков, П.И.Монастырный. Вычислительные методы высшей математики. 1972.
Дж.Ортега, У.Пул. Введение в численные методы решения дифференциальных уравнений. 1986.
Глава 1 . Решение нелинейных уравнений и систем.
§ 1. Нахождение начальных приближений.
Рассмотрим уравнение
(1.1)
Пусть это уравнение
имеет решение. Чаще всего решение не
единственное. Поэтому нам надо каким-то
образом отделить то решение, которое
нас интересует. Обычно либо уже в условии
задачи говорится о том, что в некотором
промежутке имеется единственное решение,
либо мы можем построить грубый график
функции
и
определить приближенное решение.
Пример 1.
Найти начальное приближение для уравнения
.
1-й способ:
строим график функции
и находим точки пересечения этого
графика с осью х.
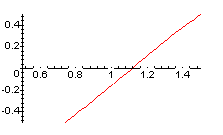
2-й способ:
переписываем уравнение в виде
,
строим графики 2-х функций
и
, затем находим точки их пересечения.
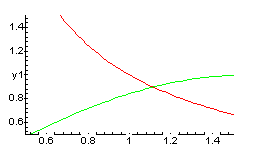
Из этих рисунков ясно, что за начальное приближение можно взять значение x 1.1 .
Пример 2. Найти начальное приближение для уравнения
.
Строим графики
двух функций
и
.
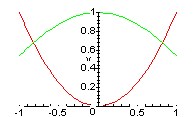
Из рассмотрения этих графиков ясно, что уравнение имеет 2 корня на промежутке
,
симметричных относительно нуля. За
начальное приближение для положительного
корня можно взять x0
= 1 .
Если уравнение имеет несколько корней, то обычно в задании указывается дополнительная информация о нужном корне.
Рассмотрим некоторые методы. Обычно используются, так называемые итерационные методы. Сущность всех этих методов состоит в том, что, зная какое-либо начальное приближение к корню или отрезок, содержащий корень, мы можем построить последовательность приближенных значений, которая сходится к корню. Способ построения такой последовательности и определяет метод. При этом нужно доказать, что построенная последовательность сходится и именно к корню.
§ 2. Простейшие итерационные методы.
Определение. Метод называется итерационным, если по одному или нескольким заданным начальным приближениям строится бесконечная последовательность приближенных решений, которая сходится к точному решению уравнения.
Метод деления отрезка пополам .
Пусть функция непрерывна на промежутке [a , b] и известно, что на [a , b] лежит только один корень уравнения . Обозначим его x* .
1-й шаг:
Полагаем
. Вычисляем
.
Если
=0,
то
—
корень уравнения и вычисления
заканчиваются. В противном случае
выполняем
2-й шаг:
Полагаем
.
Вычисляем
.
Если
,
то
—
корень уравнения, и вычисления
заканчиваются. В противном случае
повторяем 2-й шаг, где вместо
возьмем
, а вместо
получим
. Продолжая зтот процесс, получим
последовательности
. . .
. . .
Числа
и
образуют промежуток [an
, bn
], длина которого стремится к 0
при
, а
.
Имеет место оценка
.
Если мы хотим получить корень с точностью , то вычисления можно прекратить, если величина справа окажется меньше . Следовательно, мы заранее можем определить число шагов, которое нам потребуется для получения корня с заданной точностью. Это будет наименьшее целое число, которое удовлетворяет неравенству:
(2.1)
Метод хорд (секущих).
Этот метод хорошо применять для функций, монотонных в окрестности корня.
Пусть мы нашли
отрезок [a,b], внутри которого лежит один
корень уравнения
. Обозначим
и Найдем точку пересечения прямой,
проходящей через точки
, с осью х
:
(2.2)
Вычислим
.
Вычисляем точки
по правилу:
(2.3)
Заменив в формуле (2.2) a0 , b0 на a1 , b1 , найдем точку x1 и вычислим точки a2 , b2 .
Продолжая этот процесс, построим последовательность приближений x0 , x1 , ... , xi ,... по формулам
(2.4)
и точки ai и bi по следующему правилу:
(2.5)
Вычисления продолжаются до тех пор, пока при заданном малом >0 не окажется выполненным условие |xi-xi-1| < .
Рассмотрим пример.
Найти корень уравнения
.
Здесь
.
Построим график функции f(x):
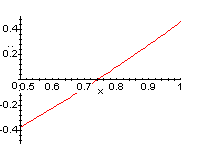
Из графика видно, что единственный корень этого уравнения лежит между 0 и /2. Можно положить a0=0, b0=/2.
Находим
.
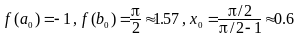Чтобы
получить следующий промежуток, подсчитаем
,
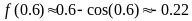т.е.
.
В качестве следующего промежутка можно
взять
.
Подсчитаем x1
и
x2
:
теперь
,
значит, следующий промежуток будет
.
Найдем x2
:
Если продолжить
вычисления, то получим
и так далее.