
- •Задача о распределении производственной программы
- •Задача о диете
- •Транспортная задача
- •§3. Графический метод решения двумерных задач линейного программирования.
- •§4. Каноническая форма задачи линейного программирования.
- •§5. Симплекс-таблица для канонической задачи.
- •Каноническая задача симплекс-таблица
- •§6. Алгоритм симплекс-метода.
- •Т. Если оптимальный план невырожденный, то он не единственный
- •§7. Метод искусственного базиса. М-метод.
- •§8. Двойственные задачи.
- •§9. Признаки оптимальности для двойственных задач.
- •§10. Целочисленное линейное программирование. Графический метод.
- •§11. Целочисленное линейное программирование. Метод Гомори.
- •§12. О параметрических задачах.
Часть 3. Методы математического программирования
§0. Оптимизационные задачи
f(x) V V (V, f, ) f –целевая функция, допустимое множество
x0 f(x0) f(x) x (V, f, )max (V, f, )min
f(x1,x2,…,xn) методы математического программирования
линейное, целочисленное, выпуклое, нелинейное программирование, вариационное исчисление, теория оптимального управления
Глава 1. Линейное и целочисленное программирование
§1. Задачи линейного программирования
V = Rn, - множество решений системы линейных уравнений и нестрогих линейных неравенств, f – линейная
а) f(x)
=
![]() б)
б)
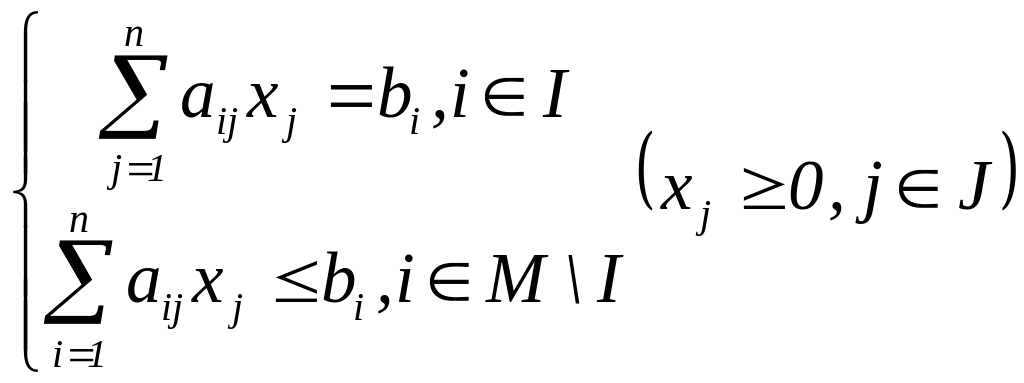 в) тип задачи, max(min)
в) тип задачи, max(min)
1. = либо выпукло 2. , f f max (оптимальное решение)
3. Оптимальное решение – на границе , если не единственно, то выпукло
§2. Примеры экономических задач.
Задача о распределении производственной программы
3 вида продукции, 2 вида ресурсов
Ресурсы |
Виды продукции |
Запасы ресурсов |
|||
I |
II |
III |
|||
1 |
а11 |
а12 |
а13 |
b1 |
|
2 |
а21 |
а22 |
а23 |
b2 |
|
Стоимость |
с1 |
с2 |
с3 |
|
|


Задача о диете
2 вида кормов Питательные вещества 1, 2, 3 не менее b1, b2, b3 ед. для нормального развития
Питательные вещества |
Корма |
Минимальная норма |
||
А |
В |
|||
1 |
a11 |
a12 |
b1 |
|
2 |
a21 |
a22 |
b2 |
|
3 |
a31 |
a32 |
b3 |
|
Стоимость |
c1 |
c2 |
|
|

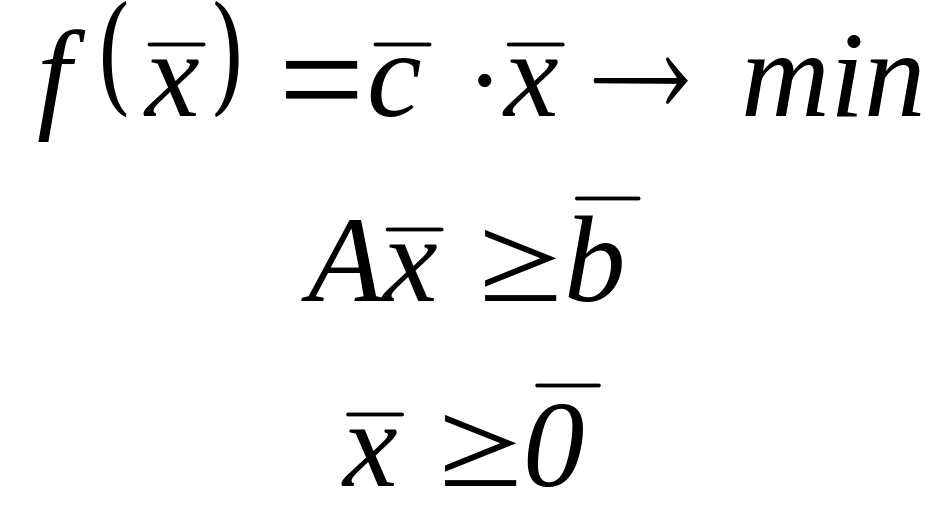
Транспортная задача
2 поставщика однородной продукции А1, А2, их запасы (мощности) а1, а2
3 потребителя этой продукции В1, В2, В3 их потребности (емкости) b1,b2,b3
cij стоимость перевозки 1 ед. продукции от Ai к Bj а1+ а2 = b1+ b2+ b3 закрытая
а1+ а2 = b1+ b2+ b3 |
B1 |
B2 |
B3 |
|
b1 |
b2 |
b3 |
||
A1 |
a1 |
c11 |
c12 |
c13 |
A2 |
a2 |
c21 |
c22 |
c23 |
![]()

§3. Графический метод решения двумерных задач линейного программирования.
2 переменных, нет ограничений-равенств f(x) = c1x1 + c2x2 max
ai1x1 + ai2x2 bi, i = 1,…,m
Пересечение 1-й четверти и полуплоскостей x1 0, x2 0
а) б) многоугольник в) неограниченное многоугольное множество
Градиент f=(c1, c2) n неизвестных, n – 2 равенства (уравнения) rank A = n – 2
§4. Каноническая форма задачи линейного программирования.
Основная задача
 Все ограничения – равенства (уравнения)
Все ограничения – равенства (уравнения)
Любая задача сводится к основной введением новых переменных в неравенствах (разность между большей и меньшей частями)
Для задачи 1 х4, х5 – остатки ресурсов, для задачи 2 (о диете) х3, х4, х5 – избыток питательных веществ сверх минимальных норм.
При неотрицательных правых частях неравенства сводятся к уравнениям с «+xi», с «xi».
Каноническая задача а) каждое уравнение содержит базисную переменную
б) правые части всех уравнений неотрицательны
f(x) = c1x1 + c2x2 + c3x3 + c4x4 max
a11x1 + a12x2 + x3 = b1 Каноническая задача всегда имеет план
a21x1 + a22x2 + x4 = b2 Базисный план канонической задачи (0, 0, b1, b2)
x1 0, x2 0, x3 0, x4 0 Базисных планов много
Оптимальный план следует искать среди базисных
