Третій основний алгоритм множення

Третій основний алгоритм множення Z= X*Y можна отримати за рекурентною формулою добутка

Z_i = Z_i-1 2 + x_i 2 ^{– n} Y, i = де Z₀ = 0, Z_n = Z.

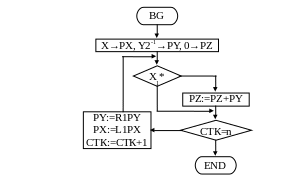
В відповідності з цією формулою множення починається зі старших розрядів множника, сума часткових добутків зсувається вліво, число кроків множення дорівнює n, закінчується виконання алгоритму додаванням. Довжину в 2n розрядів повинен мати тільки регістр PZ. ГСА алгоритму має вигляд:

Проте оскільки зсуви в РХ та PZ виконуються в одну й ту ж сторону, то в варіантах цього алгоритму старші розряди добутку можна заносити в регістр РХ.

Приклад цифрової діаграми множення чисел Х=11/16 та Y=10/16, n=4

x1*PX	PY	PZ	СТК	Пояснення
1011 0110 1100 1000	1010 1010 1010 1010	00000000 1010	001 010 011 100 END	Початковий стан +Y Результат сумування Зсув Зсув +Y Результат сумування Зсув +Y Результат сумування
		00001010 00010100 00101000 1010
		00110010 01100100 1010
		01101110

Четвертий основний алгоритм

По четвертому основному алгоритму множення Z =X*Y зводиться до обчислювання за рекурентною формулою

Z_i = Z_i-1 + x_i Y_i, i = де Z₀ = 0, Z_n = Z. Y₀ = Y, Y_i = Y_i-12^-1.

Тут множення починається зі старших розрядів множника, сума часткових добутків нерухома, в процесі множення множене зсувається вправо, закінчується множення додаванням. Очевидно, що довжину в 2n розрядів тут повинні мати регістри PY та PZ. Оскільки сума часткових добутків нерухома, то використовувати для зберігання її частини регістр РХ, що звільняється, неможливо. Проте закінчення операції можна визначати за нулоьвим вмістом РХ і, таким чином, виключити СТК. Відмінностями на ГСА, як і при множенні за другим основним алгоритмом, буде заміна умови СТК = n умовою PX = 0 та вилучення елементарних операцій на СТК. ГСА такого множення має вигляд:

Цифрова діаграма множення чисел Х = 7/16; Y = 15/16, n = 4.

x1*PX	PY	PZ	СТК	Пояснення
0111 1110 1100 1000	01111000 00111100 00011110 00001111	00000000 00000000 00111100	001 010	Початковий стан Зсув +Y Результат додавання Зсув +Y Результат додавання Зсув +Y Результат додавання
		00111100 00111100 00011110	011
		01011010 01011010 00001111	100
		01101001	END

T = (n-1)(t_з+t₊)+t₊