Нескінчено малу функцію в точці ще називають нескінчено малою величиною.

Приклад 1. Нехай . Тоді

Отже, функція в точці є нескінчено малою.

Приклад 2. Нехай . Тоді Отже, задана функція в точці є нескінченно малою.

Якщо - внутрішня точка інтервалу , то, використавши означення границі функції в точці, нескінчену малу функцію можна означити так.

Означення 2. Функція називається нескінчено малою в точці , якщо для будь-якого числа існує число таке, що для всіх  , які задовольняють нерівність , виконується нерівність .

Аналогічно можна означити нескінчено малу функцію на нескінченості.

Означення 3. Функція називається нескінченно малою на нескінченності ), якщо для будь-якого числа існує таке число , що для всіх , які задовольняють нерівність , виконується нерівність .

Приклад 3. Розглянемо функцію . Тоді Отже, функція на нескінченності є нескінчено малою.

Нескінченно малі функції аналогічно до нескінчено малих числових послідовностей володіють аналогічними властивостями.

Примітка 1. Іноді доводиться розглядати не одну, а кілька нескінченно малих функцій у даній точці. Такі функції порівнюють між собою за допомогою границі їх відношення, і залежно від того як поводить себе таке відношення поблизу даної точки, нескінченно малим величинам дають певну назву.

Подамо ряд означень.

Нехай і є нескінченно малі функції в точці

 ( може бути і нескінченно віддаленою точкою).

Означення 4. Якщо , то називається нескінченно малою вищого порядку малості, ніж . При цьому називається нескінченно малою нижчого порядку малості, ніж .

Приклад 4. Нехай , Тоді і в точці є нескінченно малі функції. Знайдемо

Отже, в цьому випадку є нескінчено мала вищого порядку, ніж .

Приклад 5. Нехай ,

Тоді

тобто і на нескінченності є нескінченно малі функції. Знайдемо

Отже, функція є нескінченно мала вищого порядку, ніж при або, що те саме, є нескінчено мала нищого порядку, ніж при .

Означення 5. Якщо де С- відмінне від нуля число, то і в точці називаються нескінчено малими однакового порядку малості.

Якщо при цьому , то і в точці називаються еквівалентними і записують ~ (при ).

Приклад 6. Нехай , а Тоді і в точці є нескінченно малі функції. Оскільки

то ~ (при .

Означення 6. Якщо і є нескінченно малі функції в точці і ,де - довільне число, а число , то функція називається нескінченно малою порядку по відношенню до .

Приклад 7. Нехай , а . Оскільки

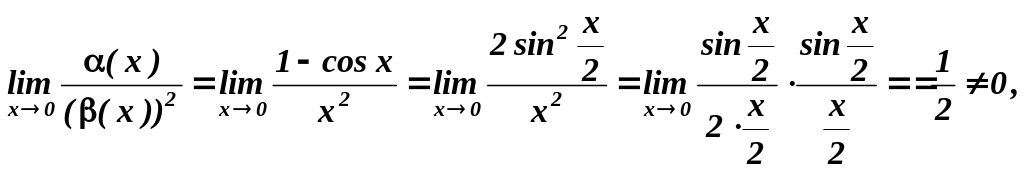то функція у точці є нескінченно малою другого порядку по відношенню до

§5. Неперервність функції

5.1. Означення неперервності функції в точці і на відрізку

Означення 1. Нехай функція f(x) визначена в околі точки. Функція називається неперервною в точці x₀, якщо границя функції f(x) при існує і дорівнює значенню в точці , тобто

Це означення вимагає виконання таких трьох умов:

1. f(x) повинна бути визначена в деякому околі точки x₀.

2. Існує скінчена границя

3. Ця границя повинна дорівнювати значенню функції . f(x₀).

Означення 2. Нехай функція f(x) визначена в околі точки . Функція називається непе–рервною в точці x₀., якщо для довільного як завгодно малого додатного , можна вказати таке що з нерівності випливає нерівність

Якщо вираз назвати приростом аргументу , а вираз - приростом функції, то на основі означення 1 можна формулювати інше означення неперервності функції в точці .

Означення 3. Нехай функція визначена в околі точки . Функція є неперервною в точці , якщо в цій точці нескінчено малому приросту аргументу відповідає нескінчено малий приріст функції , тобто

Означення 4. Нехай функція визначена на проміжку Функція називається неперервною зліва в точці , якщо .

Означення 5. Нехай функція визначена на проміжку . Функція називається неперервною справа в точці , якщо .

Означення 6. Функція називається неперервною на відрізку , якщо вона неперервна в кожній точці інтервалу Неперервна зліва в точці і неперервна справа в точці .

Примітка. Сума, різниця, добуток декількох неперервних в деякій точці функцій є неперервні в цій точці. Якщо знаменник не перетворюється в нуль у точці неперервності, то частка двох неперервних в цій точці функцій є неперервною функцією.

5.2. Класифікація точок розриву функції

Означення 7. Якщо в точці функція не є неперервною, то точка називається точкою розриву функції.

Виходячи з означення 1 неперервності функції в

точці , точка буде точкою розриву функції, якщо не виконується одна з трьох умов:

1) у точці функція невизначена;

2) у точці не існує границі ;

3) існує границя , але вона не дорівнює значенню функції .

Існують такі типи розривів :

1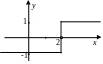 ) Розрив 1-го роду. Якщо існують скінчені ліва і права границі ( і ), але вони не рівні між собою.

Наприклад, функція

має при

розрив 1-го роду (див. мал.)

т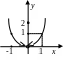 ому, що існують скінчені границі але ці границі не рівні між собою.

2) Якщо лівостороння і правостороння границі і в точці рівні між собою, тобто , але не дорівнюють значенню функції в точці тобто .

Наприклад, функція

має в точці розрив, тому що але ці границі не дорівнюють значенню в точці

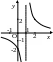Р озрив 2-го роду. Якщо лівостороння або правостороння границі функції у точці дорівнюють , то кажуть, що функція має в точці розрив другого роду.

Наприклад, функція має в точці розрив 2-го роду, бо