§ 10. Матричний метод

Нехай задана система лінійних алгебраїчних рівнянь з невідомими (1.4).

Позначимо через матрицю, складену із коефіцієнтів при невідомих (так звану основну матрицю системи); матрицю-стовпець із невідомих; - матрицю-стовпець із вільних членів, тобто

Тоді систему рівнянь (1.4) можна переписати у вигляді матричного рівняння:

Якщо квадратна матриця має не нульовий визначник , то для неї існує обернена . Помноживши зліва в цьому рівнянні на , одержимо або . Враховуючи, що і , одержимо матричний розв’язок системи

Знаходження матричного розв’язку називається матричним способом розв’язування системи лінійних алгебраїчних рівнянь.

Приклад 1. Записати і розв’язати в матричній формі систему рівнянь

Розв’язування. Позначимо через

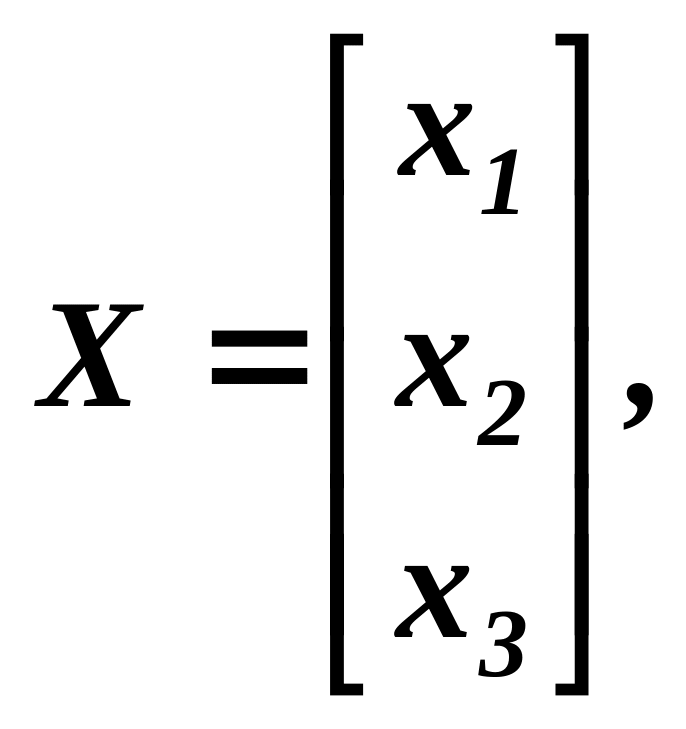
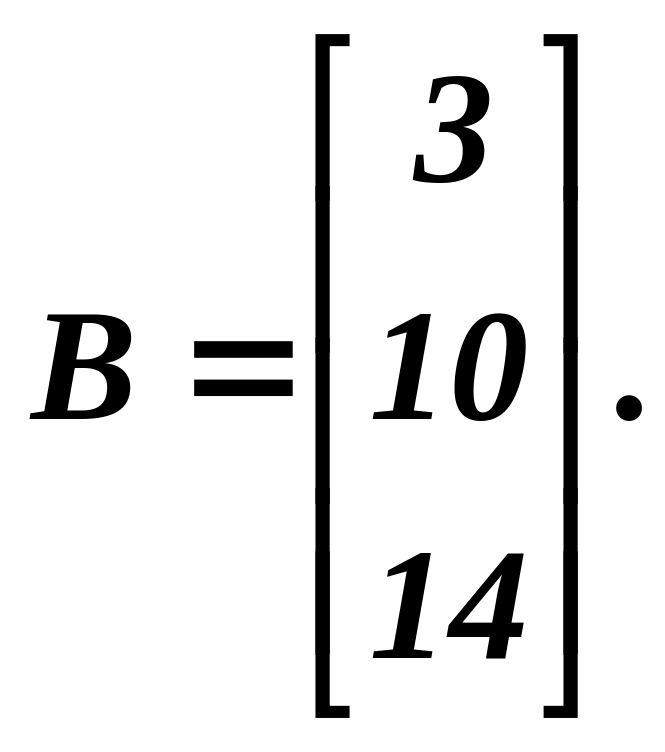
Система лінійних рівнянь запишеться у матричній формі Матричний розв’язок системи буде

Для знаходження оберненої матриці обчислимо визначник

Оскільки , то для матриці існує обернена , а значить можна знайти єдиний розв’язок вихідної системи.

Знайдемо алгебраїчні доповнення до елементів заданої матриці:

Складемо матрицю з цих алгебраїчних доповнень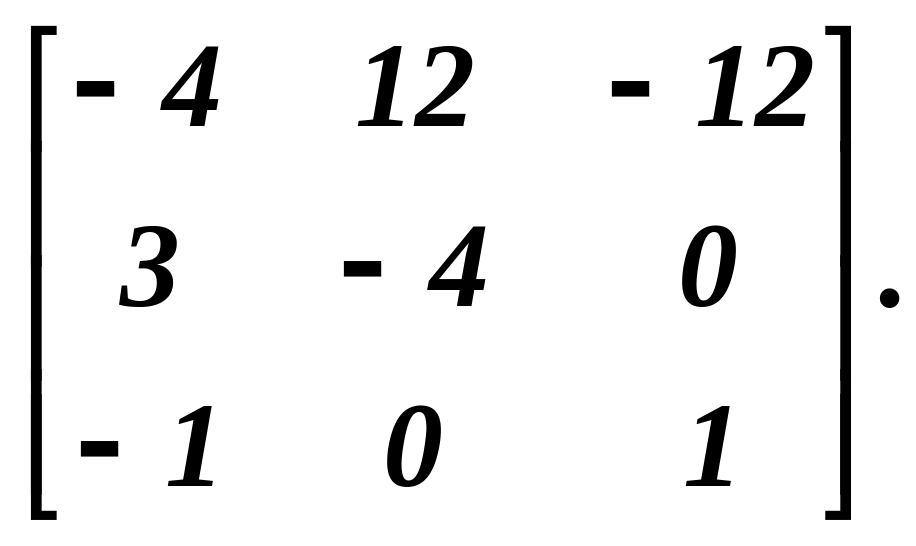

Транспонуючи її, запишемо приєднану матрицю

Обернена матриця має вигляд

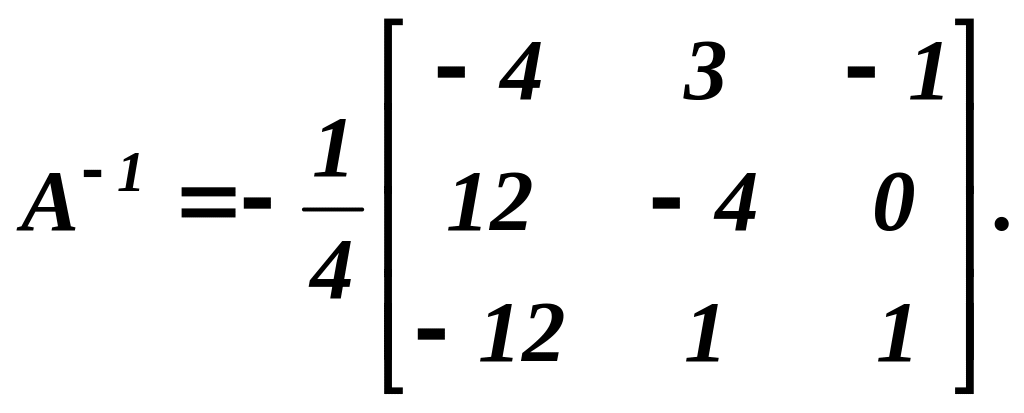
Знайдемо розв'язок заданої системи:

Розв’язок системи лінійних рівнянь такий:

§11. Метод Гаусса

Задана система лінійних алгебраїчних рівнянь з невідомими (1.4).

Вважаємо, що коефіцієнт . В іншому випадку, переставим місцями такі довільні два рівняння, щоб в першому із них був коефіцієнт біля , що не дорівнює нулю.

Метод Гаусса розв’язування системи лінійних алгебраїчних

рівнянь полягає в послідовному виключенні невідомих. Покажемо суть цього методу.

Поділимо перше рівняння на коефіцієнт а₁₁ і позначимо

.

Далі від другого рівняння віднімемо перше рівняння, помножене на ; від третього рівняння віднімемо перше, помножене на і т.д. В результаті одержимо нову систему лінійних алгебраїчних рівнянь, в якій виключено з усіх рівнянь, починаючи з другого:

Тут -

нові коефіцієнти і вільні члени, які одержались після перетворень за формулами:

,

.

Далі, виключимо з усіх рівнянь, починаючи з третього. Поділимо друге рівняння на Якщо цей коефіцієнт то переставимо місцями довільні рівняння так, щоб коефіцієнт біля був не нульовим.Позначимо

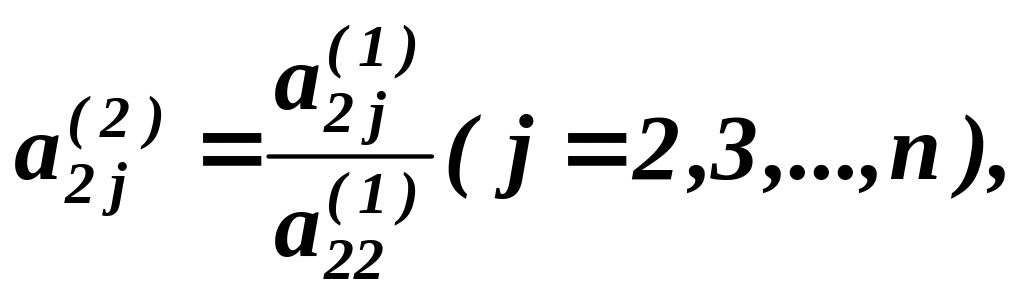
Від третього рівняння віднімемо друге рівняння, помножене на , від четвертого рівняння віднімемо друге, помножене на і т.д. Одержимо нову систему лінійних алгебраїчних рівнянь, яка еквівалентна попередній:

Такий процес будемо продовжувати до того часу, поки система не набуде трикутного вигляду:

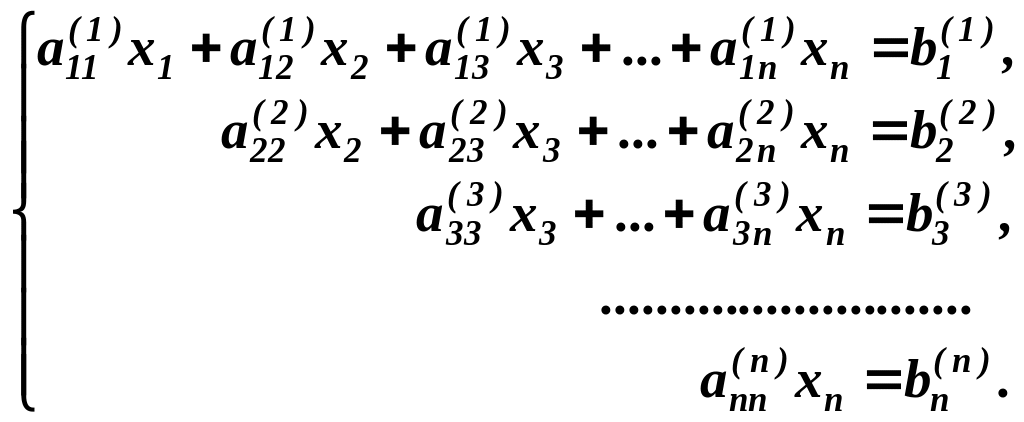
Тут і в попередній системі коефіцієнти біля ,а також вільні члени одержуються в результаті перетворень:

,

.

При цьому коефіцієнти

Остання система містить n лінійних рівнянь і n невідомих і має єдиний розв’язок. Перехід від першої системи рівнянь до останньої називається прямим ходом методу Гаусса. Обернений хід методу Гаусса починається з останньої системи рівнянь. Її розв’язують , знайшовши з останнього рівняння x_n. Підставивши це значення в передостаннє – знайдемо x_n-1 і т.д. З першого рівняння знаходять x₁.

Зауваження 1. Якщо в результаті перетворень зустрінеться хоч одне рівняння вигляду 0∙x₁+0∙x₂+…+0∙x_n=0, то одержимо систему лінійних рівнянь:

Тут

Залишаємо в лівих частинах рівнянь доданки, які містять k змінних, а інші доданки перенесемо в праву сторону.

Змінним величинам, які знаходяться в правій стороні надаємо довільних значень. Одержимо систему k лінійних рівнянь, які мають k невідомих і трикутний вигляд.

Таким чином, кожній комбінації змінних відповідає один розв’язок останньої системи. В цьому випадку вихідна система рівнянь має безліч розв’язків.

Зауваження 2.Якщо в результаті перетворень зустрінеться хоч одне рівняння вигляду , то вихідна система лінійних алгебраїчних рівнянь несумісна.

Приклад 1. Користуючись методом Гаусса, розв’язати систему рівнянь

Розв’язування. Першим рівнянням краще вибирати те, в якому коефіцієнт при невідомому x₁ рівний одиниці. Для цього ліву і праву частини першого рівняння можна поділити на “2”. Однак в даному прикладі зручніше поміняти місцями перше та друге рівняння:

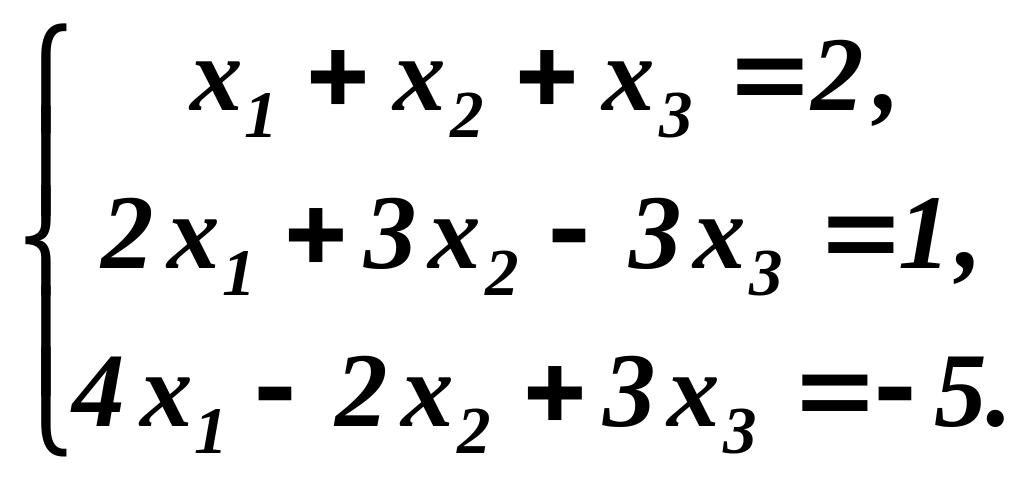
Виключимо невідоме x₁ в другому та третьому рівняннях системи.Для цього перше рівняння помножимо на “-2”, “-4” і додамо відповідно до другого та третього рівнянь:

Для виключення невідомого x₂ в третьому рівнянні додамо до нього друге, помножене на “6”:

Із останнього рівняння знаходимо Підставивши значення x₃=1 в друге рівняння, одержимо x₂= –3+5 x₃–3+5=2.

Із першого рівняння x₁=2–x₂–x₃=2–2–1= –1.

Таким чином, числа –1;2;1 є розв’язком вихідної системи лінійних рівнянь.

Часто на практиці замість перетворень над системою виконують відповідні перетворення над матрицею, складеною з коефіцієнтів при невідомих і стовпця з вільних членів, який для зручності виділимо вертикальною лінією. Таку матрицю називають розширеною матрицею системи.

Приклад 2. Користуючись методом Гаусса, розв’язати систему рівнянь

Розв’язування. Заданій системі лінійних рівнянь відповідає розширена матриця

Зведемо її до трикутного вигляду з допомогою елементарних перетворень.

1-й крок. Поміняємо місцями перший та другий рядки.

2-й крок. Додамо до елементів другого, третього і четвертого рядків елементи першого рядка, помножені відповідно на “−2”,“−2”,“−1”.

3-й крок. Додамо відповідні елементи другого і третього рядків.

4-й крок. Поділимо всі елементи четвертого рядка на “-2” і поміняємо місцями з третім рядком.

5-й крок. Додамо до елементів четвертого рядка відповідні елементи третього рядка, помножені на “6”.

6-й крок. Поділимо всі елементи четвертого рядка на “-7”.

Р

Останній розширеній матриці відповідає система рівнянь

1

2

3

4

5

озглянуті кроки зобразимо у вигляді схеми.

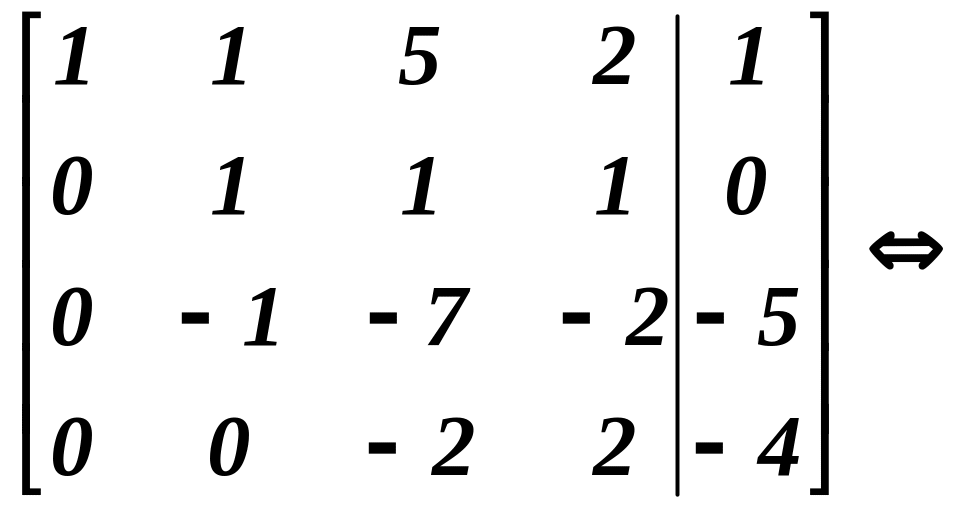
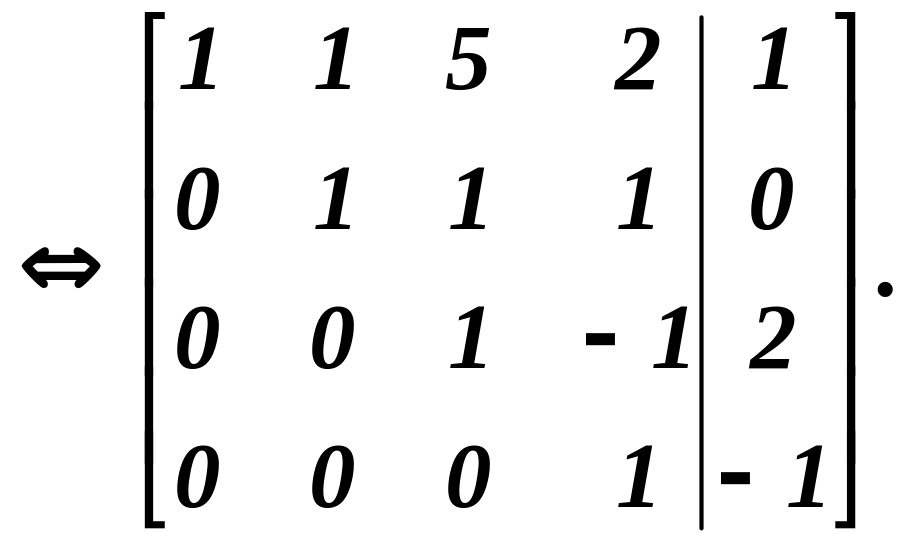
6

розв’язок якої буде розв’язком вихідної системи. Оскільки то з третього рівняння

Підставивши знайдені значення в друге

рівняння, знайдемо

Із першого рівняння одержимо

Розв’язком системи будуть такі числа:

Приклад 3. Користуючись методом Гаусса, розв’язати систе-

му рівнянь:

Розв’язування.Виключимо невідому величину із другого і

третього рівнянь. Для цього перше рівняння помножимо на “-3” і додамо до другого і третього рівнянь:

Для виключення величини віднімемо із третього рівняння подвоєне друге рівняння:

Ця система лінійних рівнянь має безліч розв’язків. Перенесемо невідому величину в праву сторону

Звідси , а із першого рівняння

Це загальний розв’язок вихідної системи рівнянь. Для отримання одного із часткових розв’язків, надамо змінній довільного значення. Наприклад, якщо , то Детальніше про розв’язування рівнянь такого типу буде показано в §13 цього розділу.

Приклад 4. Користуючись методом Гаусса, розв’язати систему рівнянь

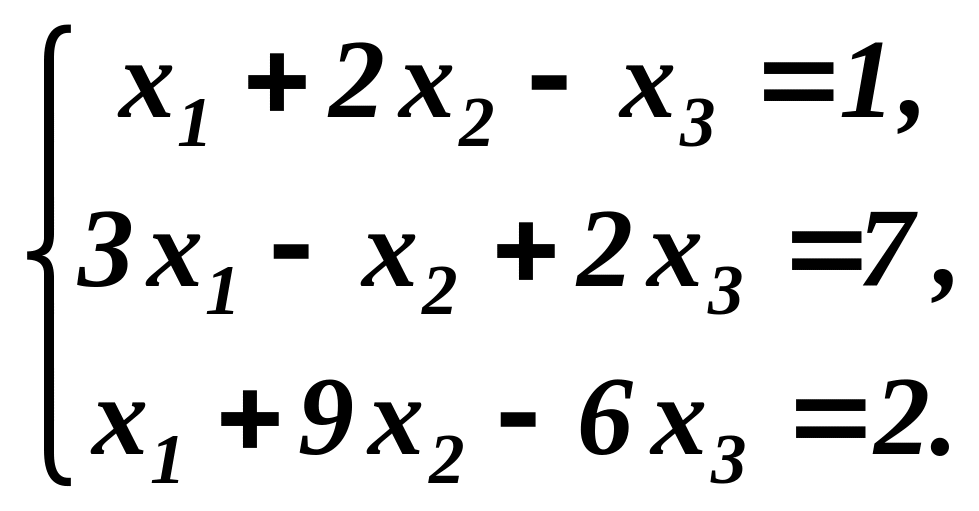
Розв’язування. Помножимо перше рівняння на “-3”і “-1” і додамо відповідно до другого і третього рівнянь. Цим самим виключимо невідому величину із другого і третього рівнянь:

Для виключення невідомої величини із третього рівняння, додамо до нього друге:

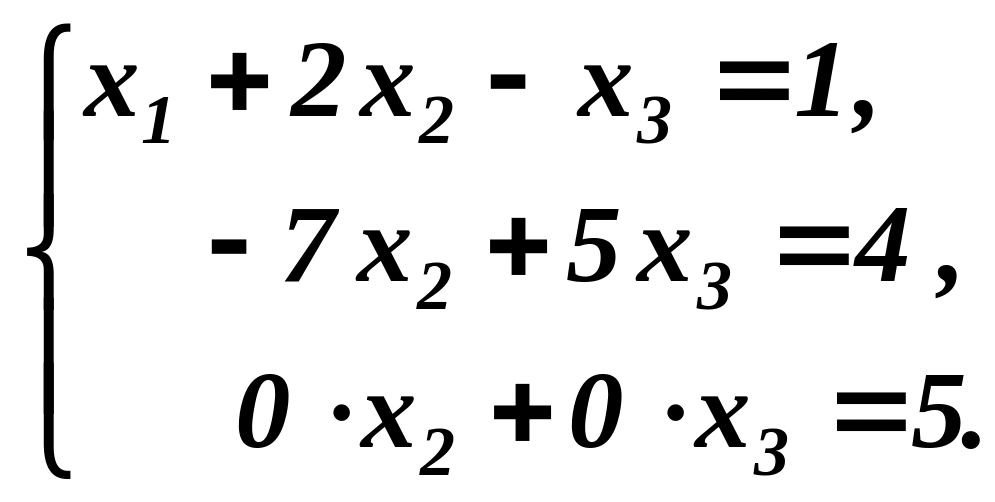
Згідно з зауваженням 2, така система лінійних алгебраїчних рівнянь несумісна.