§ 8. Системи лінійних алгебраїчних рівнянь

Рівняння називається лінійним, якщо воно містить невідомі величини тільки в першому степені і не містить їх добутки. Це рівняння такого вигляду:

, де - довільні дійсні числа.

Розглянемо систему m лінійних алгебраїчних рівнянь з n невідомими:

(1.3)

Тут числа називаються коефіцієнтами біля невідомих , а - вільними членами.

Перший індекс “ ” біля коефіцієнтів вказує, в якому рівнянні знаходиться коефіцієнт, а другий “ ” при якому із невідомих він знаходиться.

Означення. Розв'язком системи лінійних алгебраїчних рівнянь (1.3) називається така впорядкована сукупність чисел , яка при перетворює кожне з рівнянь системи в правильну рівність.

Якщо праві частини всіх рівнянь системи дорівнюють нулю, то систему рівнянь називають однорідною і неоднорідною, якщо

Якщо система лінійних алгебраїчних рівнянь має хоч один розв’язок, то вона називається сумісною, в іншому випадку – несумісною.

Якщо розв’язок системи єдиний, то система лінійних рівнянь називається визначеною. У випадку, коли розв’язок сумісної системи не єдиний, систему рівнянь називають невизначеною.

Дві системи лінійних рівнянь називаються еквівалентними (або рівносильними), якщо всі розв’язки однієї системи є розв’язками другої, і навпаки.

Еквівалентні (або рівносильні ) системи отримуємо з допомогою еквівалентних перетворень. До еквівалентних перетворень системи відносяться:

1) переставлення місцями рівнянь;

2) множення (або ділення) рівнянь на відмінне від нуля число;

3) додавання до деякого рівняння іншого рівняння, помноженого на довільне, відмінне від нуля число.

§ 9. Метод Крамера

Розглянемо систему лінійних алгебраїчних рівнянь з невідомими:

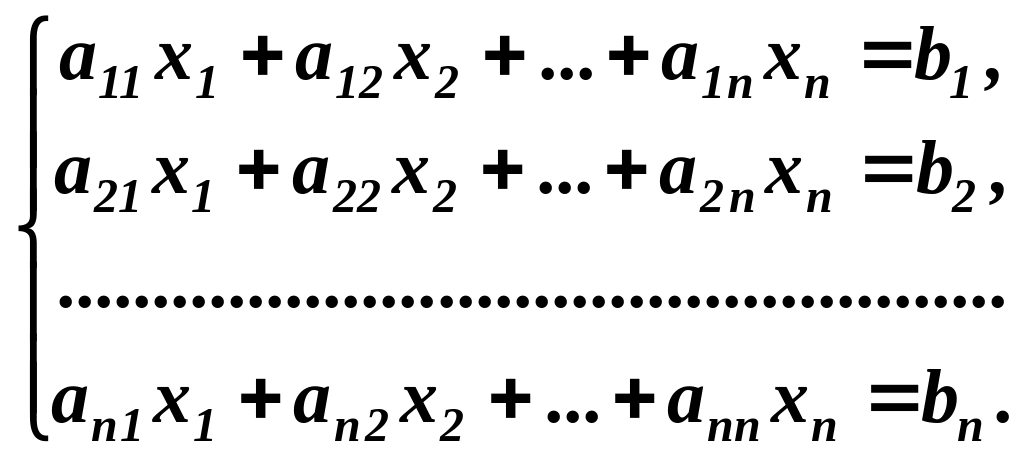(1.4)

Означення. Визначник, складений із коефіцієнтів при невідомих цієї системи

(1.5)

називається визначником системи (або головним визначником).

ТЕОРЕМА КРАМЕРА. Якщо визначник системи лінійних алгебраїчних рівнянь з невідомими відмінний від нуля ( , то ця система має єдиний розв’язок, який знаходиться за формулами Крамера:

. (1.6)

Тут - визначник, утворений із визначника заміною -го стовпця, стовпцем із вільних членів.

Доведення. Нехай - алгебраїчні доповнення елементів першого стовпця визначника системи. Помножимо перше рівняння системи лінійних алгебраїчних рівнянь з невідомими на , друге – на ,…, - не - на і додамо. Одержимо

(1.7)

Тут ( за теоремою Лапласа).

За теоремою анулювання

За теоремою заміщення

Тут .

Рівність (1.7) запишеться так: .

Оскільки , то

Так само можна показати, що мають місце інші формули із (1.6).

Приклад 1. Користуючись теоремою Крамера, розв’язати систему рівнянь :

Розв’язування. Обчислимо визначник системи

Оскільки , то задана система рівнянь сумісна і має єдиний розв’язок. Обчислимо визначники:

Значить, за формулами Крамера

Таким чином, -єдиний розв’язок системи.

Зауваження.1.Якщо і , то система лінійних рівнянь має безліч розв’язків.

Зауваження 2. Якщо і хоч один з визначників не дорівнює нулю, то система лінійних рівнянь не має розв’язків.

При розв’язуванні лінійних алгебраїчних рівнянь з невідомими за правилом Крамера потрібно обчислювати визначники -го порядку. Тому при знаходження визначників приводить до громіздких обчислень, а значить, користуватись формулами Крамера незручно.

Зауваження 3. Формули Крамера найкраще використовувати тоді, коли визначник системи , тобто коли розв’язок єдиний. Якщо кількість лінійних алгебраїчних рівнянь більша кількості невідомих, то ефективніше використовувати інші методи (методи послідовного або повного виключення невідомих), які будуть розглянуті пізніше.