Розв’язування. За ключовий елемент виберемо коефіцієнт “2” біля в першому рівнянні, оскільки він відмінний від нуля. Розділимо перше рівняння на це число “2”:

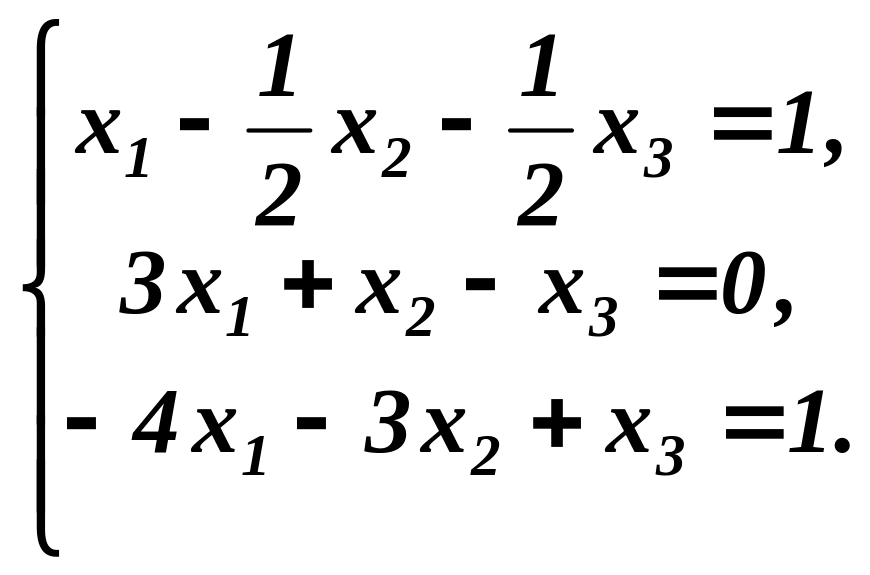
Виключимо невідоме в другому і третьому рівняннях. Для цього додамо до другого рівняння перше, помножене на “-3”, а до третього – перше, помножене на “4”.

Тобто перший крок є такий самий, як в методі Гаусса:

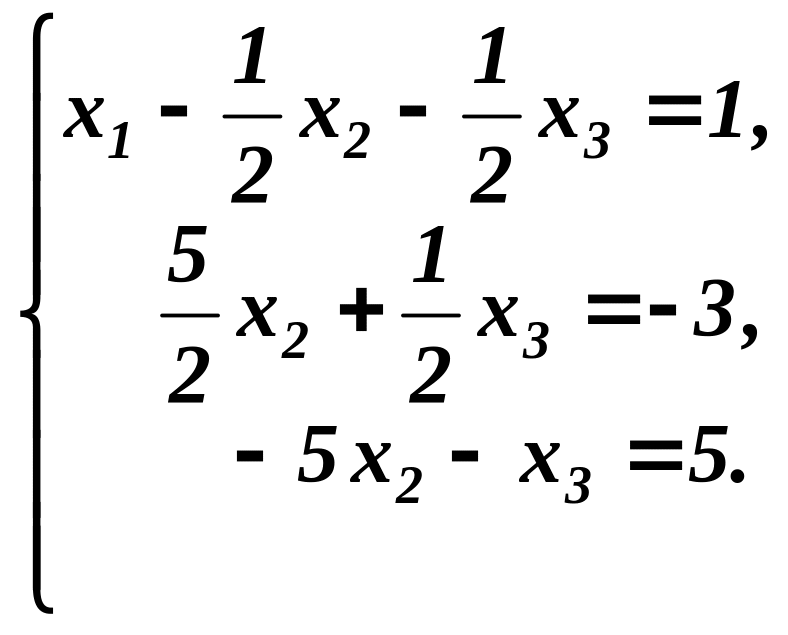
Серед двох рівнянь (друге і третє) виберемо за ключовий елемент відмінний від нуля коефіцієнт, який стоїть біля ,

Наприклад, число “ ”. Розділимо на це число друге рівняння:

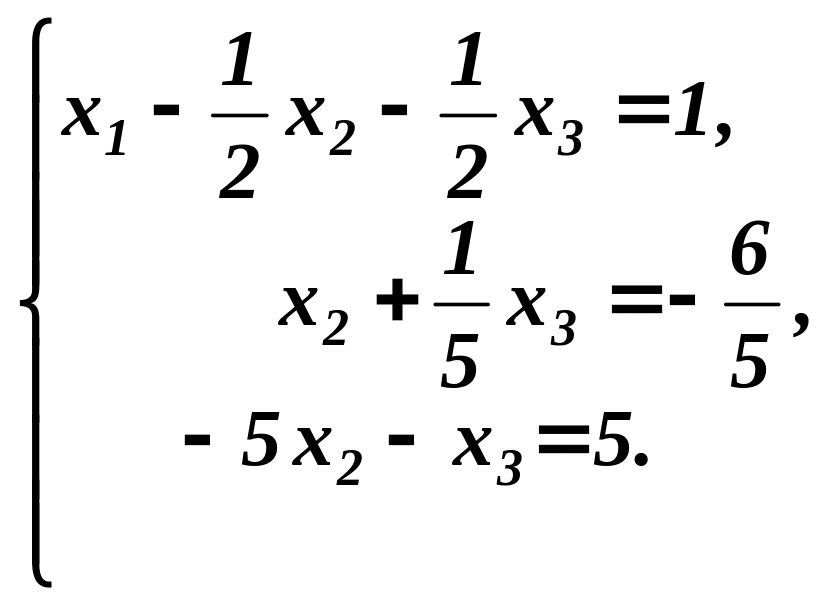
В цих рівняннях, крім другого, виключимо невідоме х₂. Для цього додамо до першого і третього рівнянь друге, помножене на “0,5” і “5”:

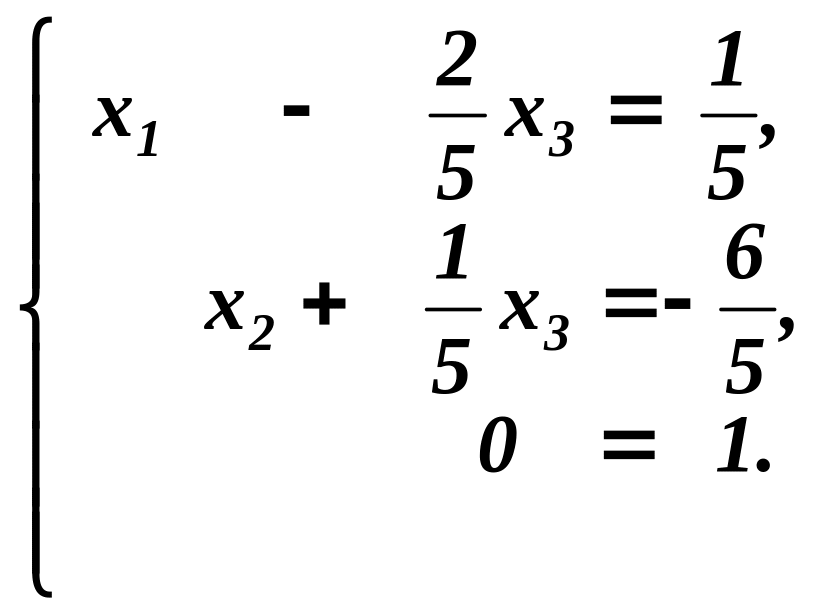
Це означає, що третьому рівнянню не можуть задовольняти жодні значення невідомих. Тобто вихідна система рівнянь розв’язків немає.

Особливо зручно користуватись методом Жордана-Гаусса в матричній формі, яка представлена таблицею. При цьому її перетворення здійснюється з допомогою певних кроків.

1. Вибираємо ключовий елемент 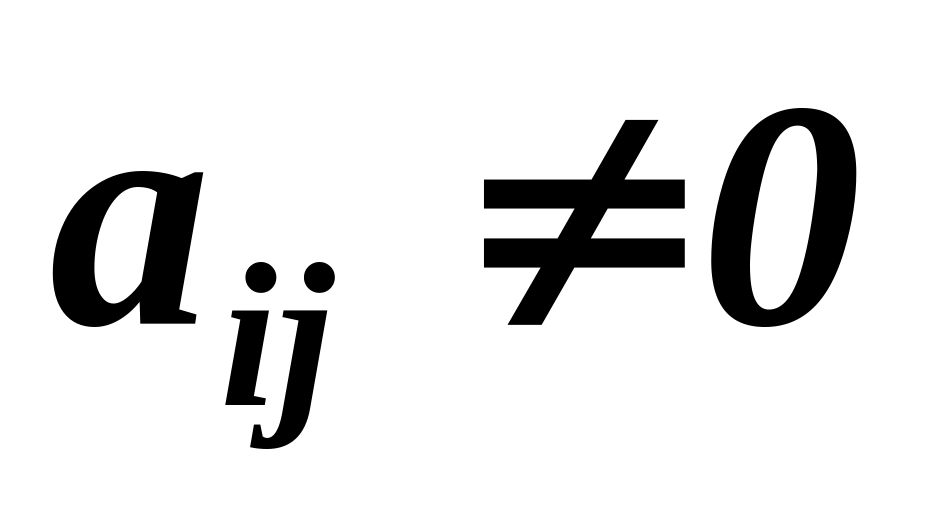. Ключовий рядок на кожному етапі вибирається інший так, щоб йому відповідала тільки одна невідома.

2. Елементи -го рядка (ключового) ділимо на і записуємо в -ий рядок наступної розрахункової таблиці.

3. Елементи ключового стовпця (крім ключового елемента, який рівний 1 ) записуємо нульовими.

4. Інші елементи наступної розрахункової таблиці (в тому числі і контрольного стовпця) обчислюємо за формулою

.

5. Порівнюємо суму елементів рядка розрахункової таблиці з відповідним елементом контрольного стовпця ( ).

Перехід від однієї матриці-таблиці до іншої за методом Жордана-Гаусса називається симплексним перетворенням матриць-таблиць.

Приклад 2. Розв’язати методом Жордана-Гаусса систему лінійних рівнянь:

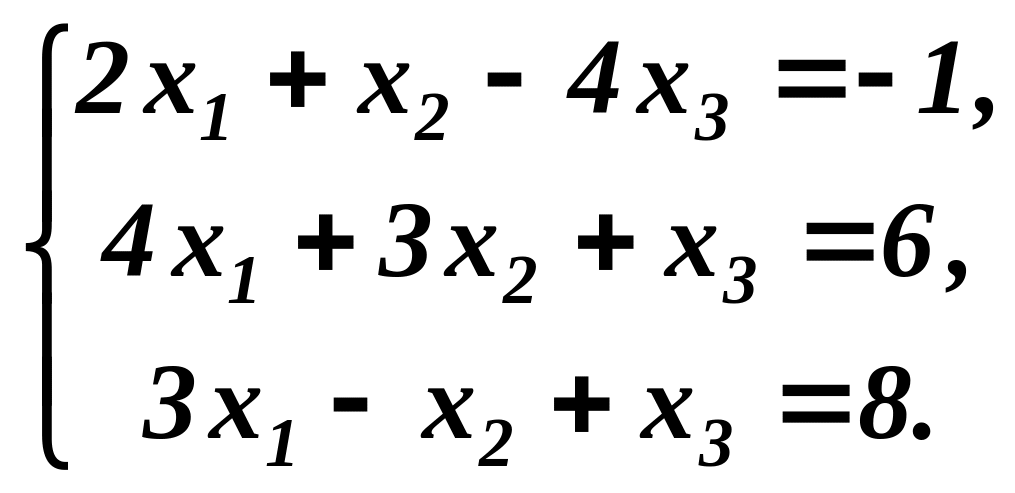
Розв’язування. Запишемо задану систему в табличній формі. За ключовий елемент тут взято коефіцієнт “2” при х₁ в першому рівнянні і взято в рамки. Стовпець ∑ є контрольним, а елементи його дорівнюють сумі інших чисел цього рядка, тобто сумі коефіцієнтів біля невідомих і вільного члена відповідного рівняння.

Таблиця 1. За ключовий елемент взято число “2”. Поділивши на нього елементи першого рядка, одержимо відповідні елементи першого рядка таблиці 2(на це вказує число “ ” в першому рядку поза таблицею).

Таблиця 2. Напроти першого рядка записано число “-4” і направлена стрілка до другого рядка табл.1. Це означає, що елементи першого рядка множаться на “-4” і додаються до відповідних елементів другого рядка табл.1. Число “-3” і стрілка, направлена до третьої стрічки означає,що на це число “-3” множаться всі елементи першого рядка табл.2 і додаються до відповідних елементів третього рядка табл.1. Цим самим в табл. 2 в першому стовпці під числом “1” отримали нульові елементи. За ключовий елемент цієї таблиці вибираємо число “1” в другому рядку (взято в рамку). Запис “ ” із стрілкою до першого рядка означає, що елементи ключового рядка другої таблиці потрібно помножити на “ ” і додати до відповідних елементів першого рядка. Цим самим отримаємо елементи таблиці 3.

Аналогічно - “ ” і стрілка до третього рядка означає множення елементів ключового рядка цієї таблиці на “ ” і додавання до відповідних чисел третього рядка для запису в

третьому рядку таблиці 3.

Результатом виконання дій цієї таблиці є виключення невідомої із другого і третього рівнянь системи.

Таблиця 3. За ключовий елемент цієї таблиці взято “ ” із третього рядка і третього стовпця (взято в рамку). Запис “ ” в цій стрічці поза таблицею означає, що всі її елементи треба помножити на це число, тобто робимо ключовий елемент одиницею. Результат множення записуємо третім рядком табл. 4. Підсумком виконання цих дій табл. 3 є виключення невідомої з першого і третього рівнянь.

Таблиця 4. Числа “-9” і “ ”, які записані справа від таблиці із стрілками до другого і першого рядків табл. 3 означають: елементи третього рядка табл.4 множимо на “-9” і “ ” і додаємо до відповідних елементів другого і першого рядків табл.3.

№ таблиці					∑
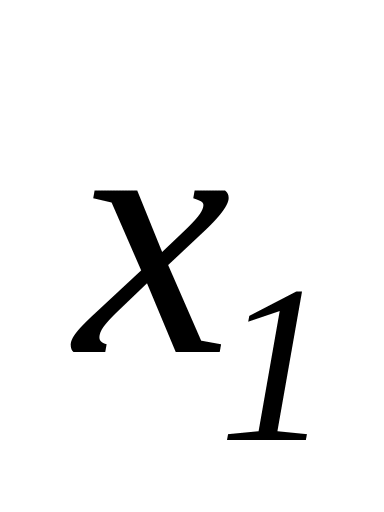
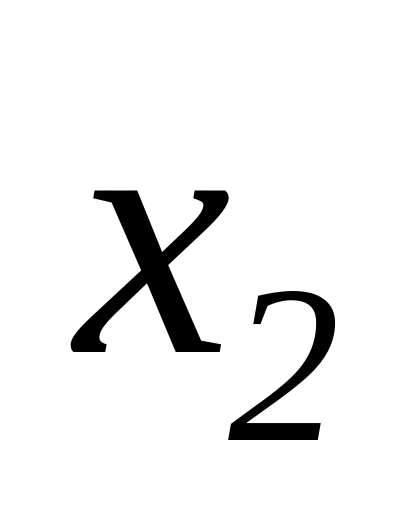
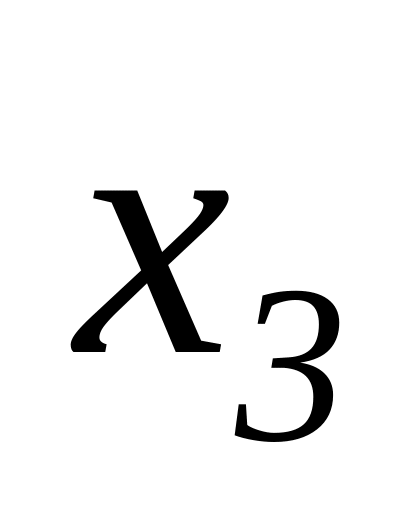
Ключовий елемент Ключовий стовпець 1	2	1	-4	-1	-2
	4	3	1	6	14
	3	-1	1	8	11
2	1	½	-2	−½	-1
	0	1	9	8	18
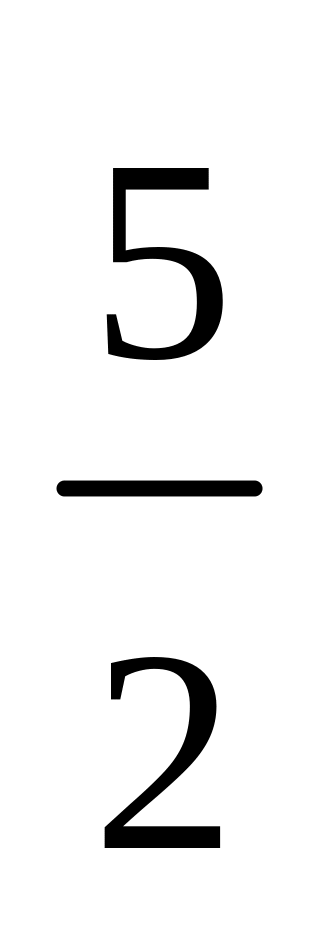
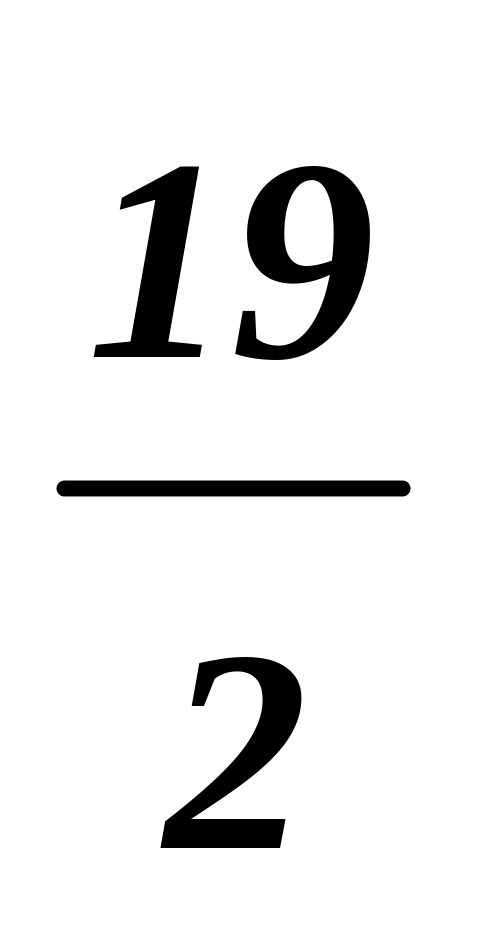
	0	-	7		14
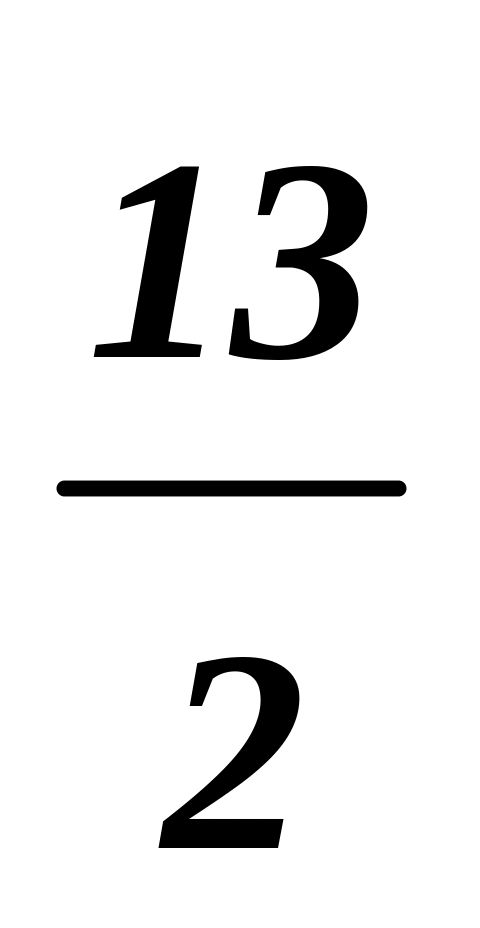
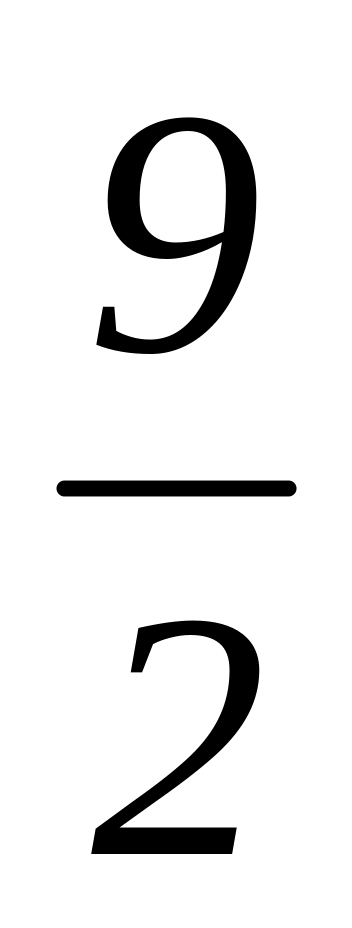
3	1	0	-	-	-10
	0	1	9	8	18
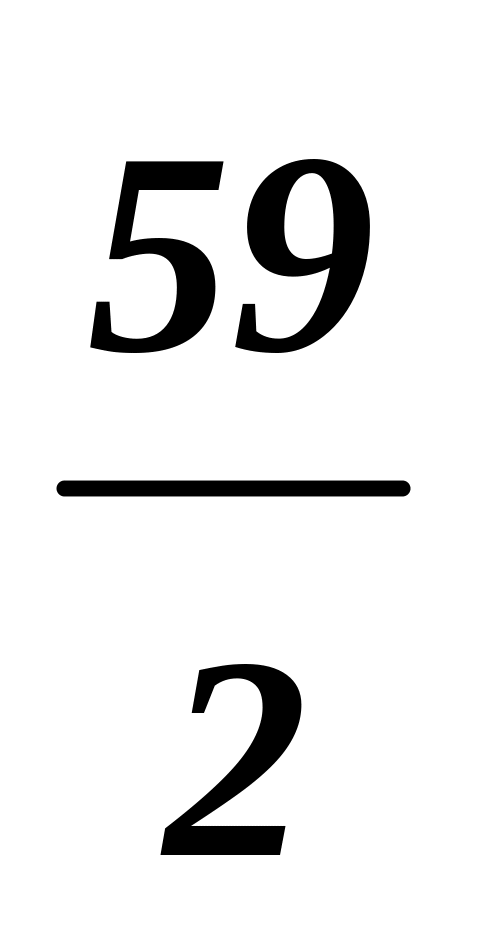
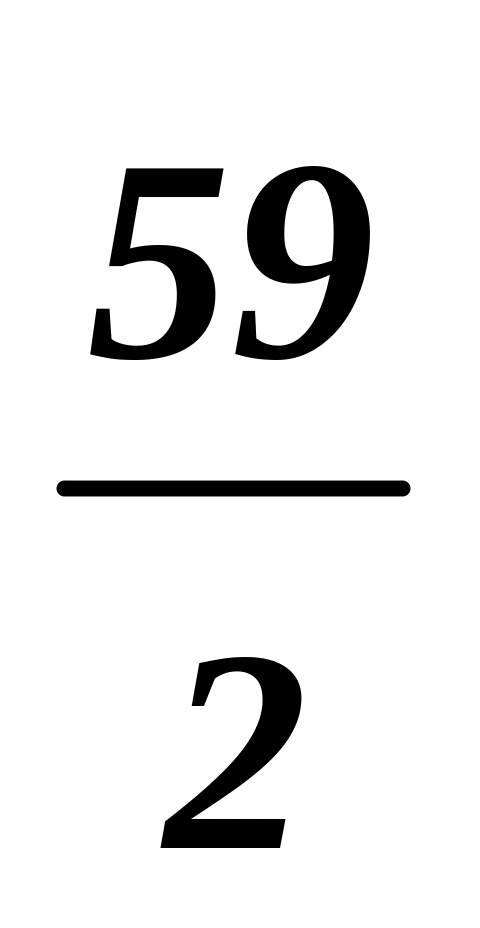
	0	0			59
4	1	0	0	2	3
	0	1	0	-1	0
	0	0	1	1	2

Останній таблиці 4 відповідає така система рівнянь:

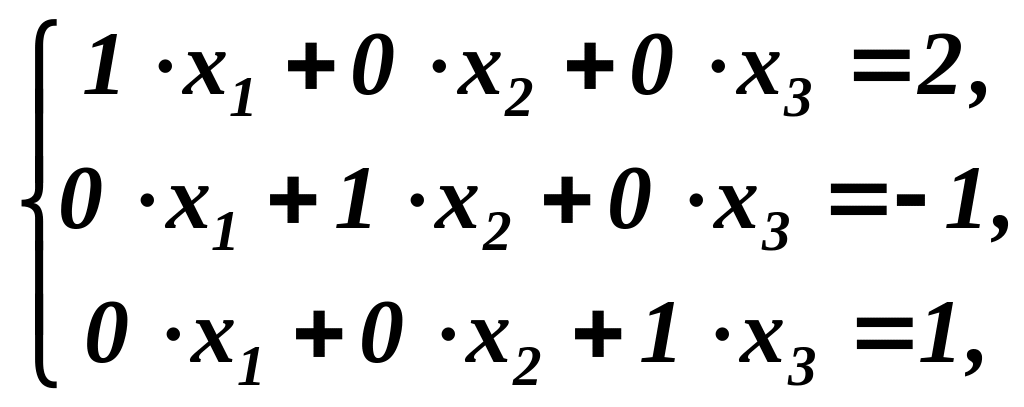
тобто є розв’язком вихідної системи трьох лінійних рівнянь з трьома невідомими.

Зауваження 1. Ключовий елемент вибирається тільки один раз у відповідному рядку або стовпці.

Зауваження 2. Ключовий елемент не вибирається серед вільних членів, тобто серед елементів

Зауваження 3. Для спрощення обчислень в якості ключового елемента доцільно вибирати найменший і не обов'язково .

Приклад 3. Розв’язати методом Жордана-Гаусса систему лінійних рівнянь:

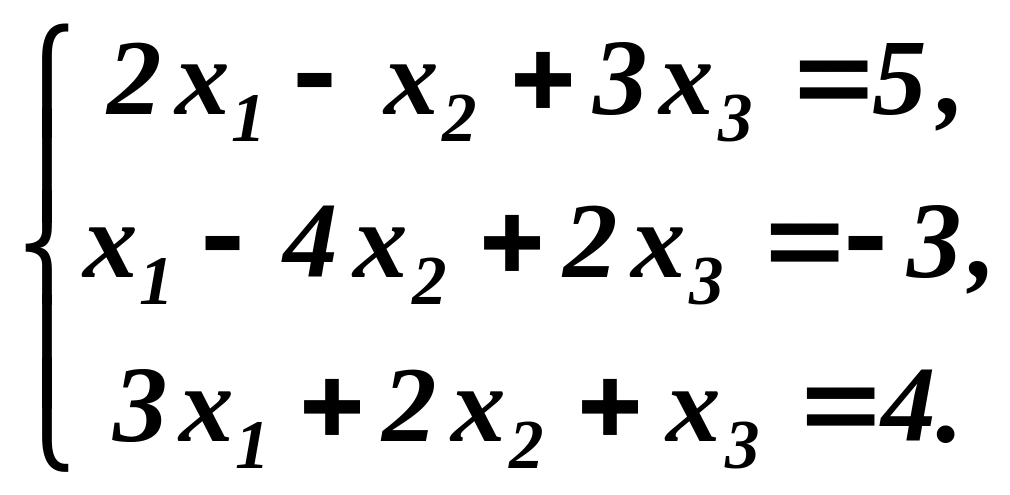
Розв’язування. Складемо таблицю із коефіцієнтів, які стоять біля невідомих і вільних членів. Стовпець  є контрольним.

№ таблиці					
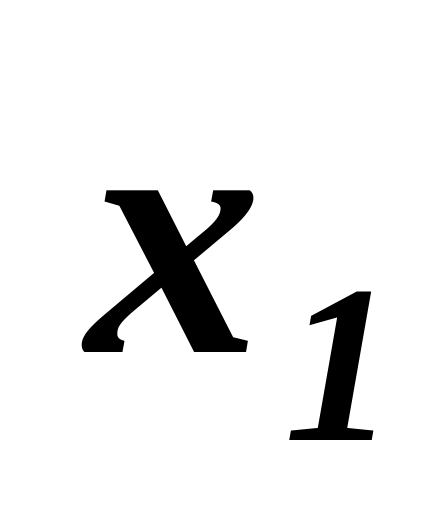
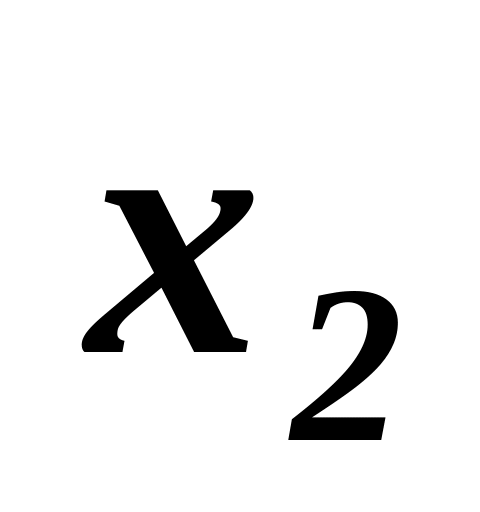
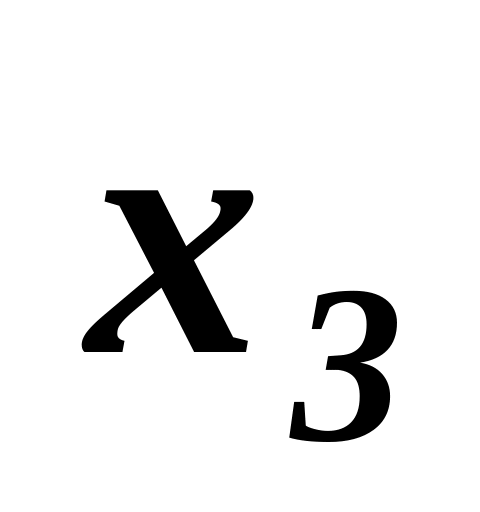
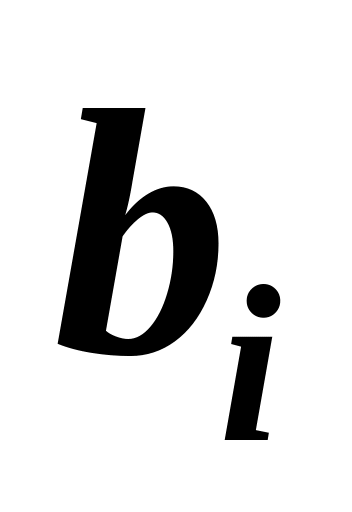
(-1) (-3) (-2), 1	2	-1	3	5	9
	1	-4	2	-3	-4
	3	2	1	4	10
(-2), (5) 2	0	7	-1	11	17
	1	-4	2	-3	-4
	0	14	-5	13	22
(- ) 3	0	-7	1	-11	-17
	1	10	0	19	30
	0	-21	0	-42	-63
(-10), (7) 4	0	0	1	3	4
	1	0	0	-1	0
	0	1	0	2	3

Рядки цих таблиць заповнювались в такій послідовності.

Таблиця 1. За ключовий елемент вибрано коефіцієнт біля x₁ другого рівняння, тобто число “1”.

Таблиця 2.

1 рядок: елементи другого рядка табл.1 множимо на “-2” і додаємо до відповідних елементів першого рядка;

2 рядок : перенесено без зміни з таблиці 1.

3 рядок: елементи другого рядка табл. 1 множимо на

“-3” і додаємо до відповідних елементів третього рядка.

За ключовий елемент в табл.2 вибираємо число “-1”, яке знаходиться в першому рядку.

Таблиця 3.

1 рядок: елементи першого рядка табл.2 множимо на “-1”.

2 рядок: елементи першого рядка табл.3 множимо на “-2” і додаємо до відповідних елементів другого рядка табл.2.

3 рядок: елементи першого рядка табл. 3 множимо на “5” і додаємо до відповідних елементів третього рядка табл.2.

За ключовий елемент цієї таблиці вибираємо число “-21”.

Таблиця 4.

3 рядок: елементи третього рядка табл.3 ділимо на “-21”.

1 рядок: елементи третього рядка табл.4 множимо на “7” і додаємо до відповідних елементів першого рядка табл.3.

2 рядок:елементи третього рядка табл. 4 множимо на “-10” і додаємо до відповідних елементів другого рядка табл.3.

Із останньої таблиці 4 випливає, що x₁= −1, x₂= 2, x₃=3.

§13. Довільні системи лінійних алгебраїчних рівнянь

Розглянемо систему m лінійних рівнянь з n невідомими (1.3).

Складемо основну ( ) і розширену ( ) матриці цієї системи:

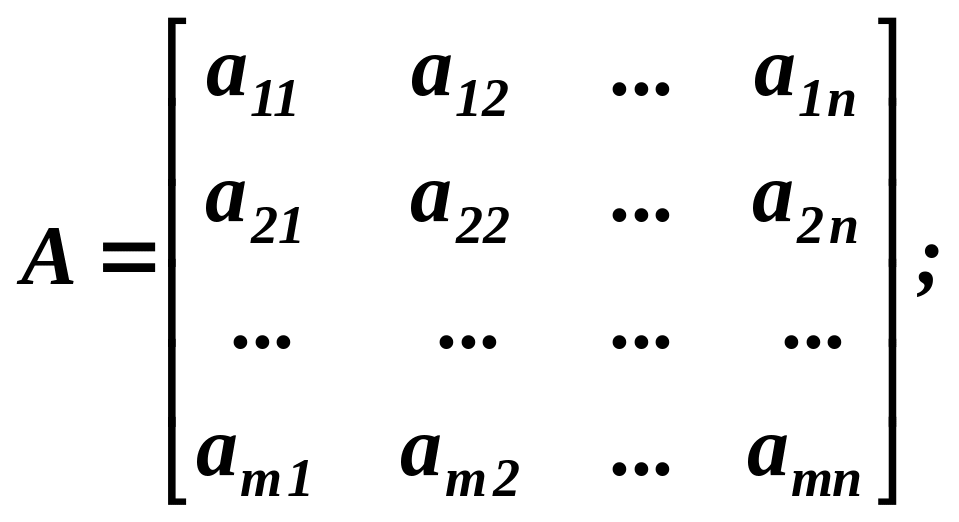
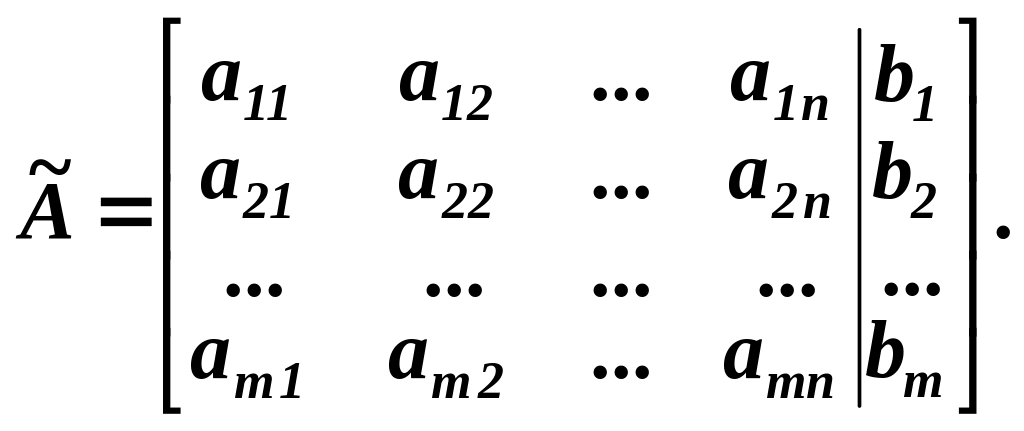
Теорема Кронекера-Капеллі. Система m лінійних рівнянь з n невідомими має розв’язок, тобто сумісна тоді і тільки тоді, коли ранг основної матриці (r(a)) дорівнює рангу розширеної матриці .

Відмітимо, що і не можуть перевищувати кількість невідомих, тобто , .

Розглянемо три випадки.

1. Якщо , то система лінійних рівнянь не сумісна.

2. Якщо , то система лінійних рівнянь сумісна і має розв’язок, який знаходиться за одним із методів, розглянутих в попередніх параграфах.

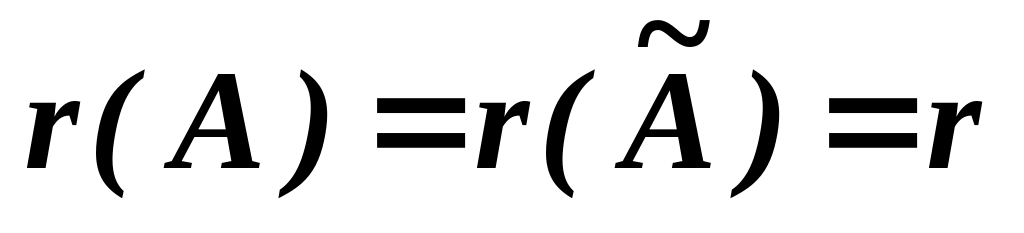3. Якщо і , то система лінійних рівнянь сумісна і має безліч розв’язків.

Базисним мінором матриці називається відмінний від нуля мінор, порядок якого рівний рангу матриці. Допустимо, що

. Для знаходження розв’язків системи візьмемо

рівнянь, в яких коефіцієнти при невідомих утворюють базисний мінор. Інші рівняння відкидаємо. Невідомі, коефіцієнти при яких утворюють базисний мінор, називають основними (або базисними) і залишають зліва. Інші невідомі називають вільними і переносять в праві частини рівнянь. Надаючи довільних числових значень вільним невідомим, знаходимо відповідні значення основних невідомих.

Приклад 1. Дослідити на сумісність систему рівнянь

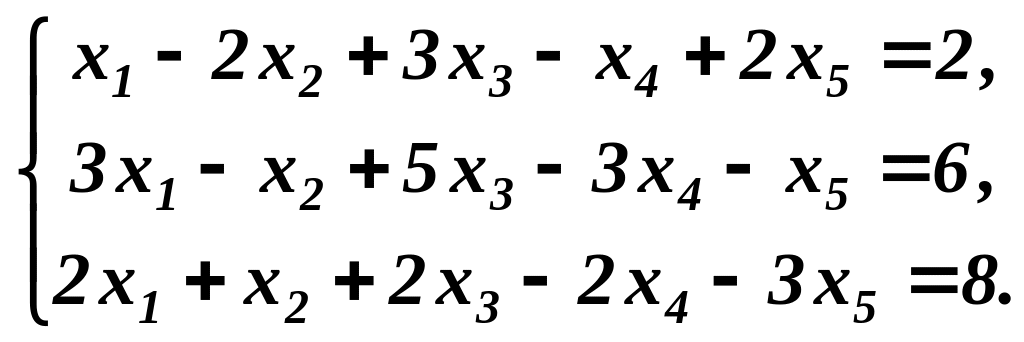
Розв’язування. Знайдемо ранги основної і розширеної матриць системи. В розширеній матриці

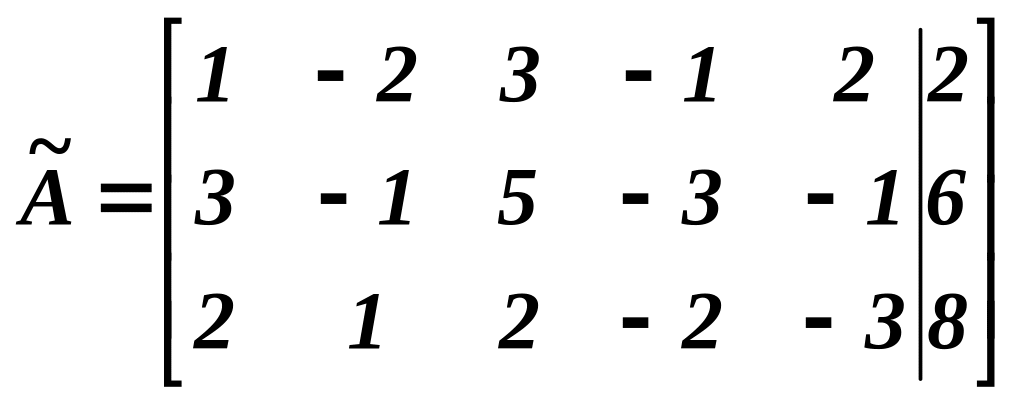
до вертикальної лінії розміщені елементи основної матриці. Тому всі елементарні перетворення, які будемо виконувати над матрицею , мають місце і для матриці :

(-3)

(-2)

(-1)

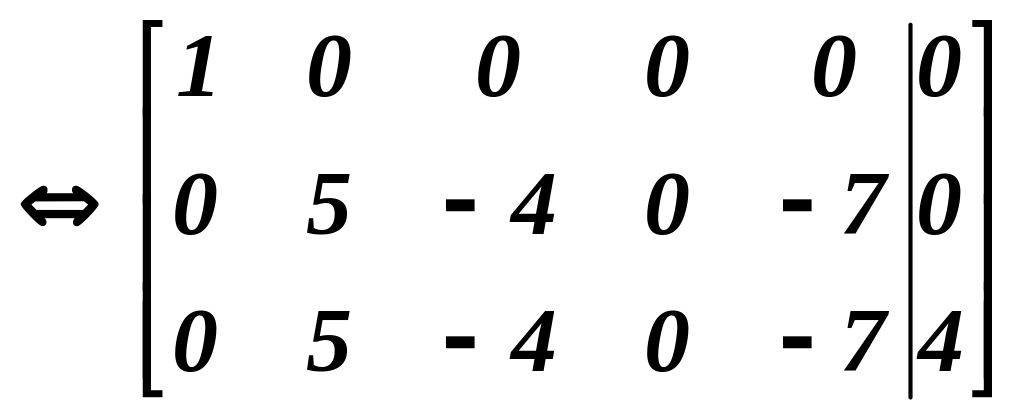
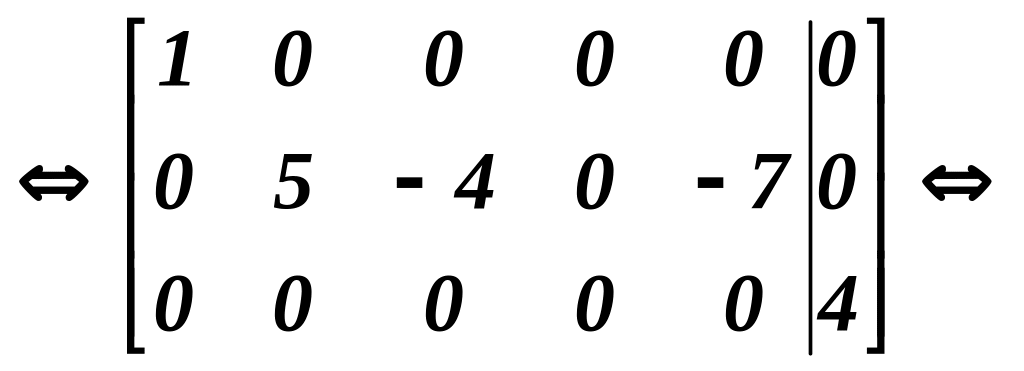
Звідси видно, що

Значить, ранг розширеної матриці рівний 3, а ранг основної

матриці - 2. За теоремою Кронекера-Капеллі система лінійних рівнянь несумісна.

Приклад 2. Дослідити на сумісність систему лінійних рівнянь і розв’язати її, якщо вона сумісна:

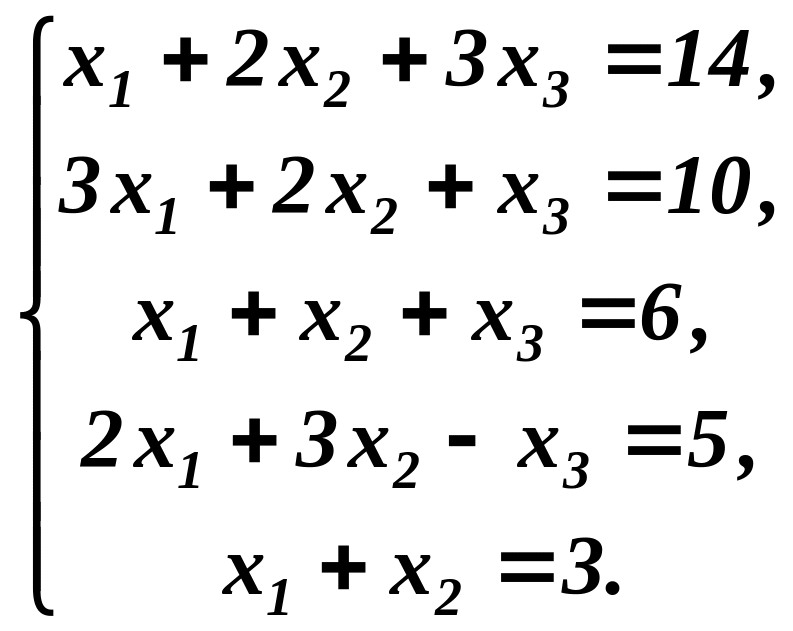
Розв’язування. Складемо розширену матрицю системи і виконаємо елементарні перетворення.

+

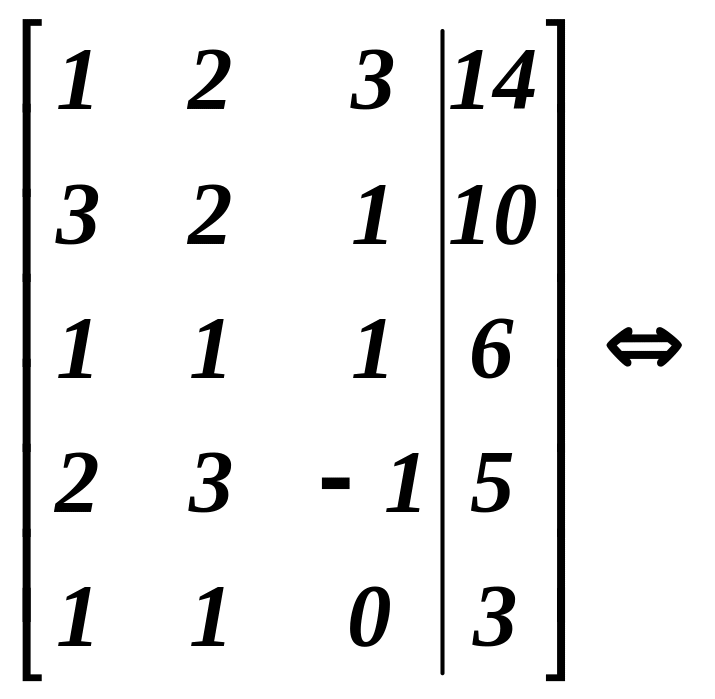
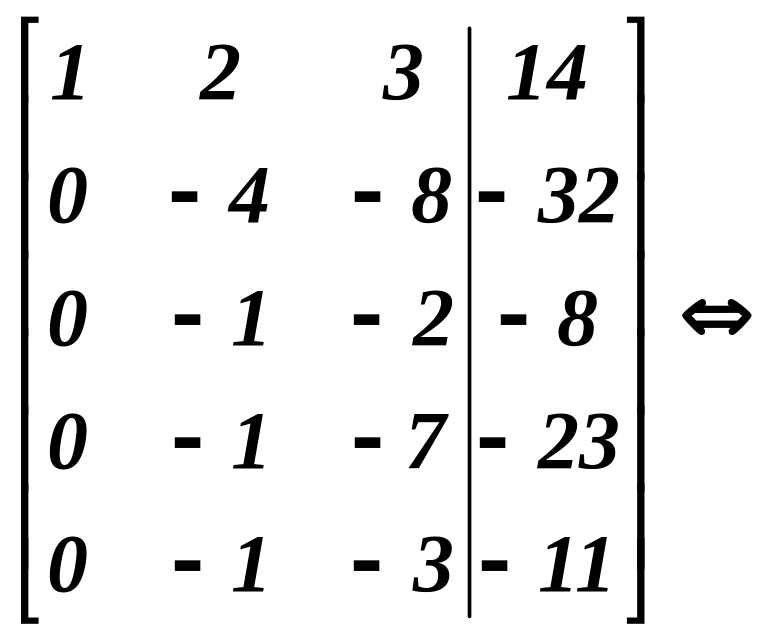
(-4) (-1) (-1)

.

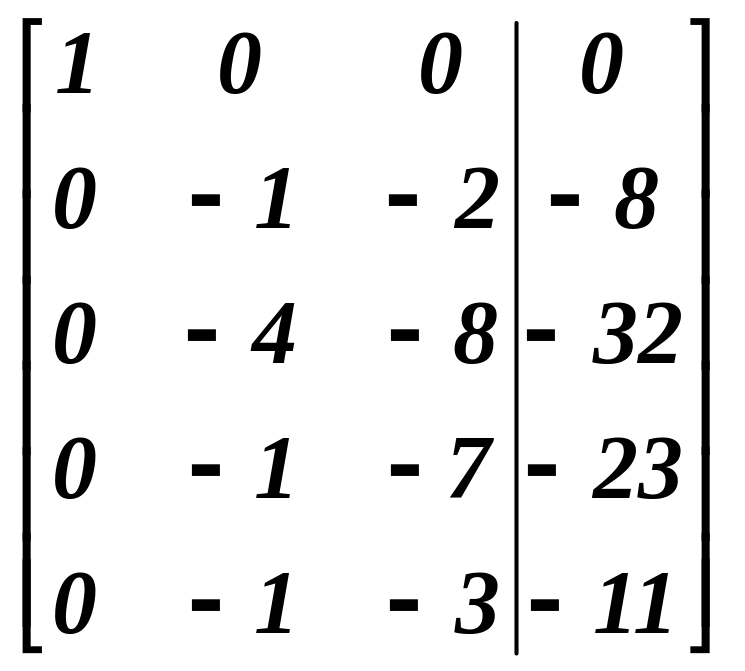
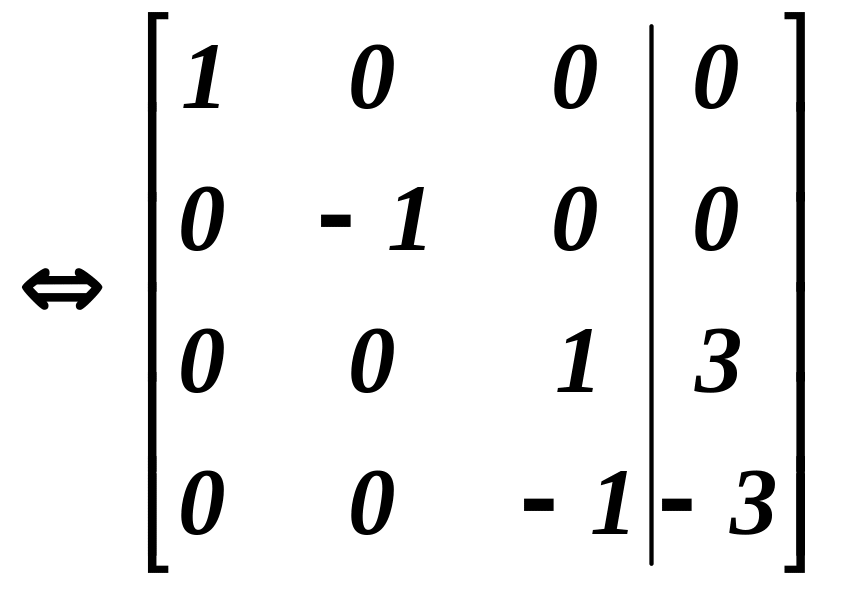
Значить r(A)=r(Ã)=3, оскільки найвищий порядок мінора як матриці А так і матриці Ã, дорівнює 3. За теоремою Кронекера-Капеллі вихідна система лінійних рівнянь має розв’язок, причому єдиний, так як кількість невідомих теж дорівнює 3.

Це означає, що два рівняння системи можна відкинути. Запишемо ті три рівняння, визначник із коефіцієнтів, які стоять біля невідомих, відмінний від нуля, наприклад

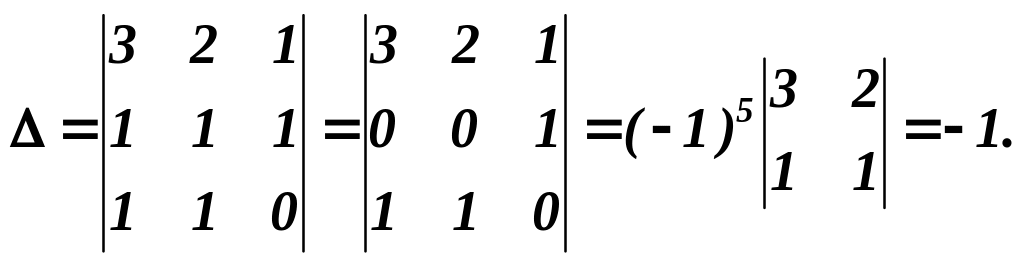
Тобто розглянемо систему рівнянь:

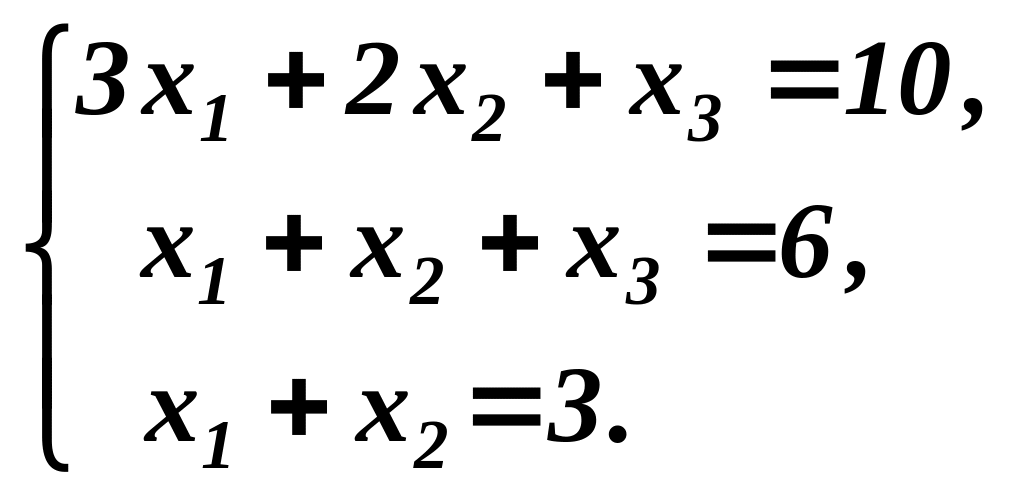
Знайдемо розв’язок цієї системи за одним із методів, наприклад, за методом Крамера. Для цього обчислимо , які одержуються з визначника системи , шляхом заміни стовпців із коефіцієнтів, які стоять біля невідомих стовпцем із вільних членів:

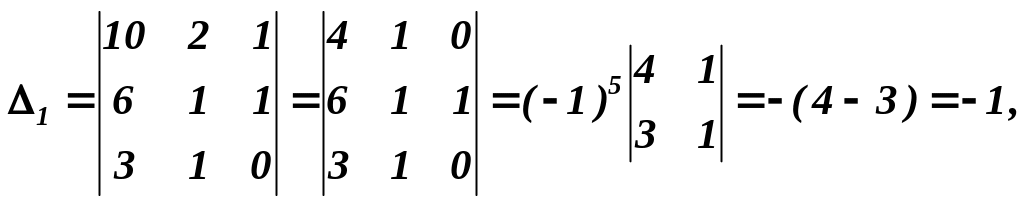
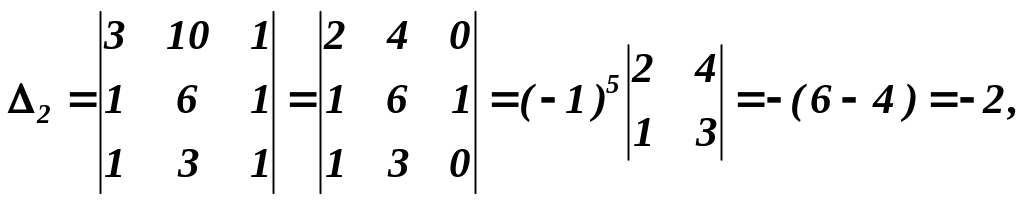
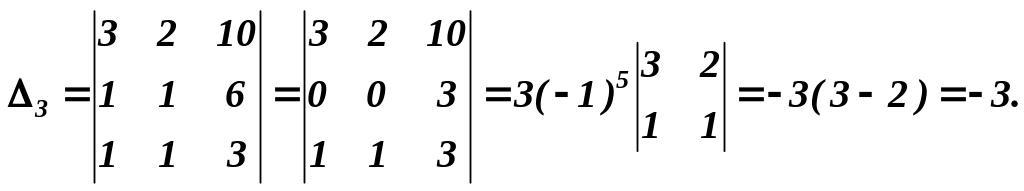
Розв’язок вихідної системи такий:

Приклад 3. Дослідити на сумісність і розв’язати систему рівнянь:

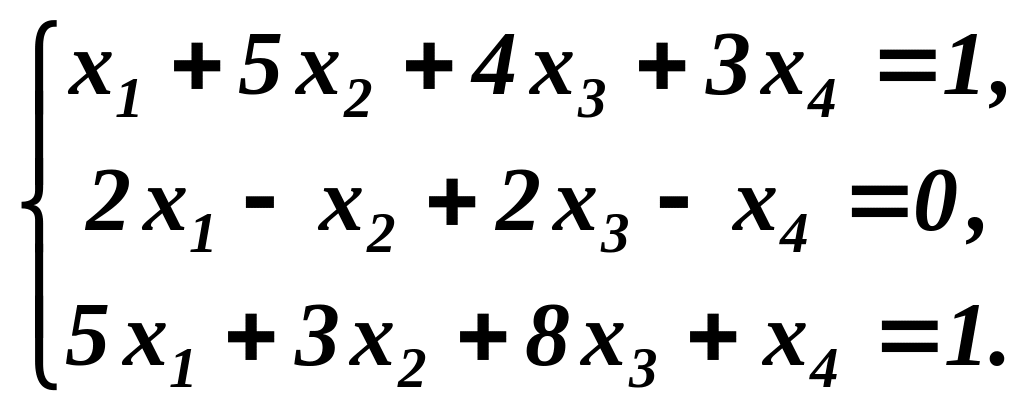
Розв’язування. З допомогою елементарних перетворень зведемо до діагонального вигляду матрицю

(-2)

(-2) (-5)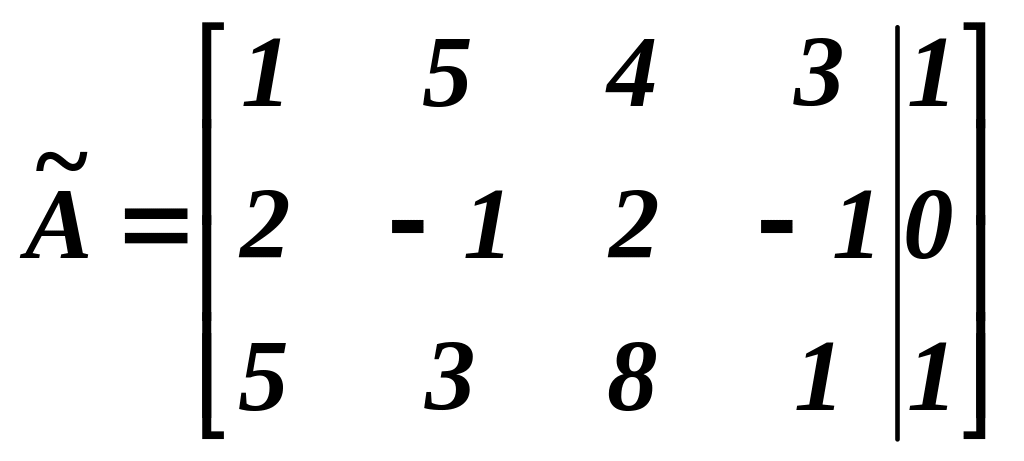

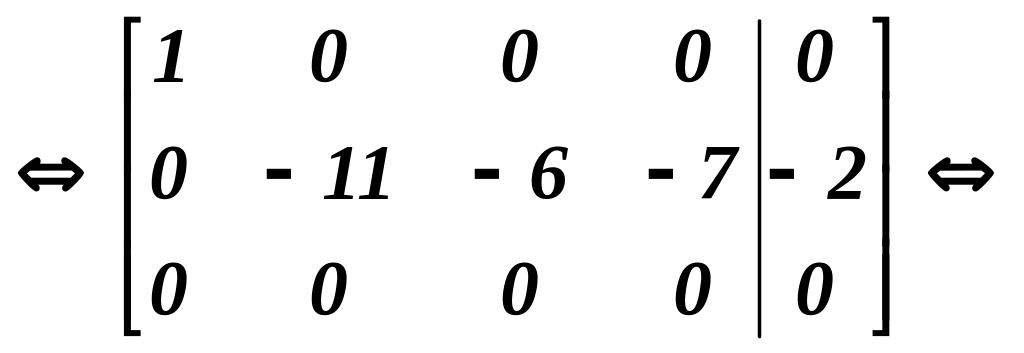
Як бачимо r(A)=r(Ã)=2. Це означає, що система лінійних рівнянь сумісна і має безліч розв’язків (оскільки ранг менший, ніж кількість невідомих).За базисний мінор візьмемо мінор 2-го порядку ( ), наприклад, який не дорівнює нулю. В даному випадку за основні невідомі приймемо х₁, х₂. Невідомі х₃ та х₄ будуть вільними.

Задана система еквівалентна такій:

або

За формулами Крамера знаходимо

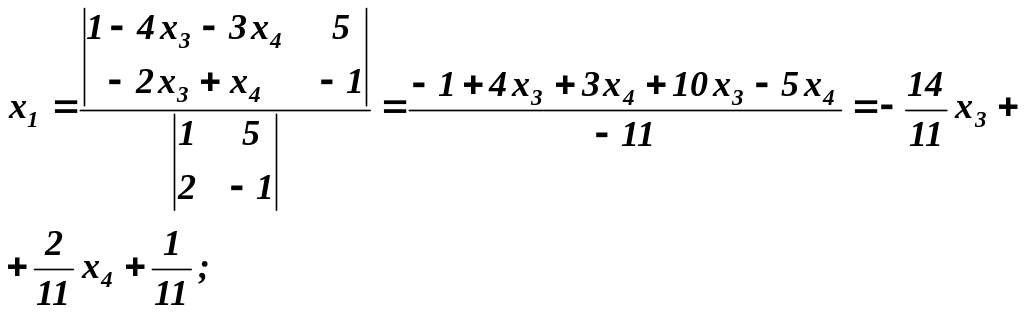
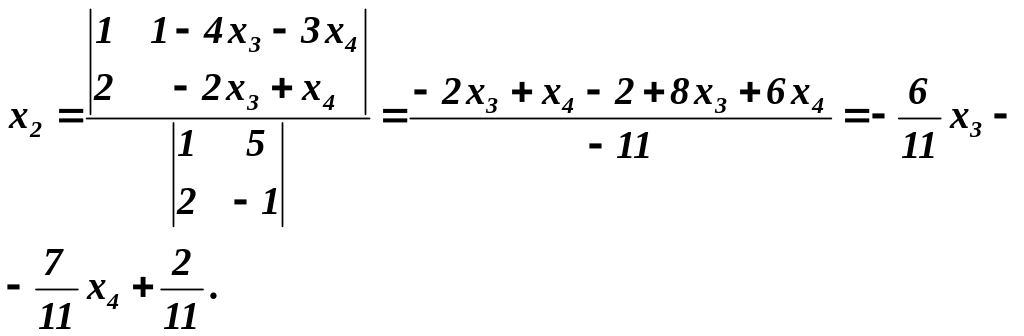
Отже, загальний розв’язок вихідної системи такий:

Надаючи вільним невідомим х₃, х₄ довільних значень, одержимо відповідні значення базисних невідомих х₁, х₂.

Наприклад, один із часткових розв’язків розглянутої системи

рівнянь буде

Зауваження. При знаходженні рангів r(A) і r(Ã) зручно користуватись методом окантування мінора. При цьому одночасно знаходимо і базисний мінор.

Системи m лінійних рівнянь з n невідомими можна розв’язувати методом Жордана-Гаусса.

Приклад 4. Дослідити на сумісність і розв’язати методом Жордана-Гаусса систему лінійних рівнянь:

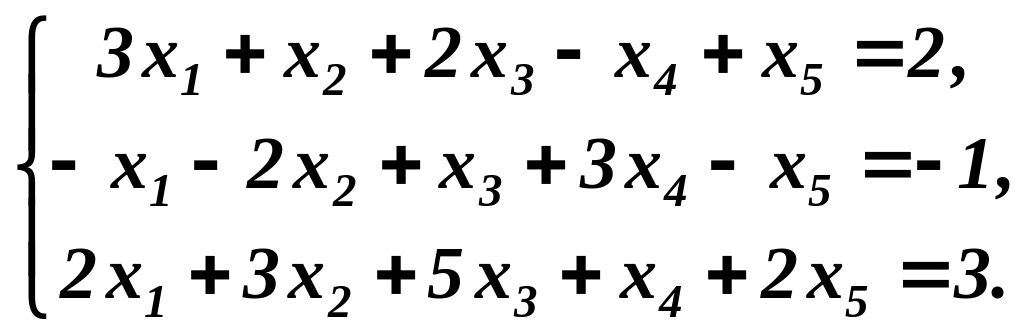
Розв’язування. Запишемо цю систему в табличній формі:

№ таблиці	х1	х2	х3	х4	х5	bi	∑
1	3	1	2	-1	1	2	8
	-1	-2	1	3	-1	-1	-1
	2	3	5	1	2	3	16
2	3	1	2	-1	1	2	8
	5	0	5	1	1	3	15
	-7	0	-1	4	-1	-3	-8
3	-11	1	0	7	-1	-4	-8
	-30	0	0	21	-4	-12	-25
	7	0	1	-4	1	3	8
(-1/30) 4	0	1	0
	1	0	0	-
	0	0	1

Дамо коротке пояснення до таблиць.

Таблиця 1. За ключовий елемент взято число “1” – коефіцієнт біля невідомої х₂. Помножимо всі елементи ключового рядка на “2” і додамо до відповідних елементів другого рядка. Помножимо всі елементи цього ж ключового рядка на “-3 ” і додамо до відповідних елементів третього рядка. При цьому отримали таблицю 2 (тут елементи першого рядка залишимо без зміни).

Таблиця 2. За ключовий елемент взято число “-1” (окреслено рамкою). Поділимо елементи ключового рядка на “-1” і утворимо нулі в третьому стовпці ( на місці елементів “2” і “5”).

Таблиця 3. Помножимо елементи третього рядка на “-5” і “-2” і додамо до відповідних елементів другого і першого рядків табл.2. За ключовий елемент візьмемо число “-30” і поділимо на нього всі елементи другого рядка і запишемо другим рядком таблиці 4.

Таблиця 4. Інші клітинки заповнимо аналогічно. Помножимо елементи другого рядка на “-7” і “11” і додамо до відповідних елементів третього і перших рядків таблиці 3.

Такі перетворення показано справа біля кожної з таблиць (числа вказують, що даний рядок на нього треба перемножити, а стрілки – до якого рядка потрібно додати відповідні елементи).

Якщо перші два рядки табл.4 поміняти місцями, то по головній діагоналі одержаної матриці-таблиці є три ненульові елементи:

1	0	0
0	1	0
0	0	1

Це означає, що ранги основної і розширеної матриць однакові

і дорівнюють 3. Тобто вихідна система 3 лінійних рівнянь з 5 невідомими сумісна і має безліч розв’язків (ранг менший за кількість невідомих).

Запишемо отриману систему базисних рівнянь, виходячи із таблиці 4.

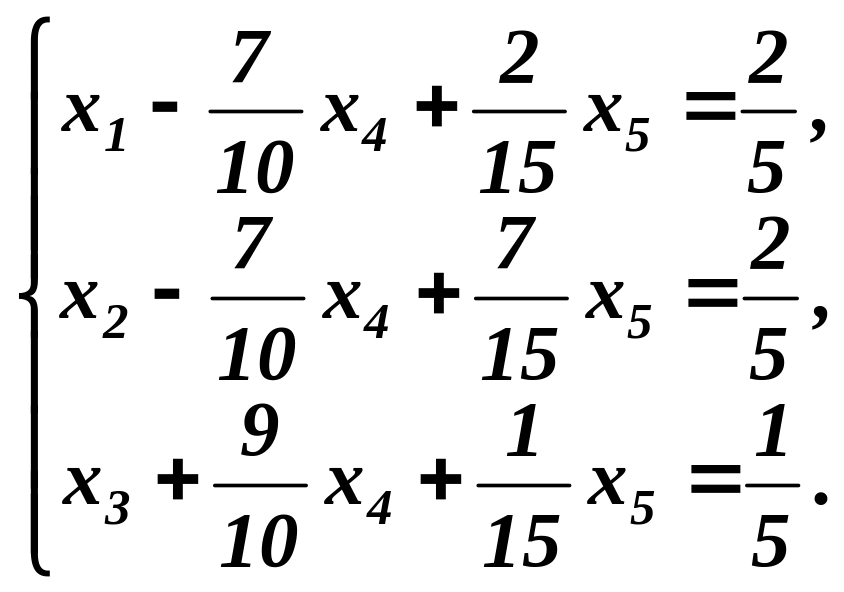
Маємо три базисні невідомі (х₁, х₂, х₃) і дві вільні (х₄, х₅). Друга таблиця виділяє базисну невідому х₂ третя таблиця - х₃ і четверта таблиця - х₁.

Звідси загальний розв’язок вихідної системи запишеться так:

.

Для перевірки правильності знайдених розв’язків, достатньо підставити ці значення х₁, х₂, х₃ у задану систему лінійних рівнянь і отримати тотожності.

Для одержання частинних розв’язків системи, надамо вільним невідомим х₄, х₅ довільних значень. Наприклад, якщо х₄=0, х₅=0,

то:

Якщо х₄=1, х₅= −1, то розв’язок буде такий:

, і т.д.

Таких частинних розв’язків можна знайти безліч.