§14. Системи лінійних однорідних алгебраїчних рівнянь

Система m лінійних алгебраїчних рівнянь з n невідомими називається однорідною, якщо вона має вигляд

(1.8)

Вона одержується із системи лінійних алгебраїчних рівнянь (1.3), якщо Розширена матриця Ã цієї системи одержується із основної матриці А, якщо приєднати нульовий стовпець. Значить ранг матриці А рівний рангу розширеної матриці Ã. При цьому за теоремою Кронекера-Капеллі вихідна система завжди сумісна.

Якщо ранг матриці системи лінійних однорідних рівнянь дорівнює кількості невідомих , то система має єдиний нульовий (тривіальний) розв’язок: Це випливає з теореми Крамера, оскільки всі визначники одержуються із визначника

(1.9)

заміною -го стовпця стовпцем із вільних членів , а тому

Значить, система лінійних однорідних алгебраїчних рівнянь з невідомими має нульові розв’язки тільки тоді, коли визначник системи , складеної із коефіцієнтів, які стоять біля невідомих відмінний від нуля.

Система лінійних однорідних алгебраїчних рівнянь з невідомими має ненульові розв’язки тільки тоді, коли визначник системи, складеної із коефіцієнтів, які стоять біля невідомих дорівнює нулю Тобто , система має ненульові розв’язки тільки тоді, коли , де - ранг матриці , а - число невідомих.

Приклад 1. Розв’язати систему лінійних однорідних рівнянь.

Розв’язування. Так як кількість рівнянь співпадає з

кількістю невідомих , а визначник

системи відмінний від нуля, то задана система лінійних однорідних рівнянь має тільки нульовий розв’язок:

Приклад 2. Розв’язати систему лінійних однорідних рівнянь

Розв’язування. Знайдемо ранг матриці, складеної з коефіцієнтів при невідомих. Для цього зведемо її до діагонального вигляду з допомогою елементарних перетворень:

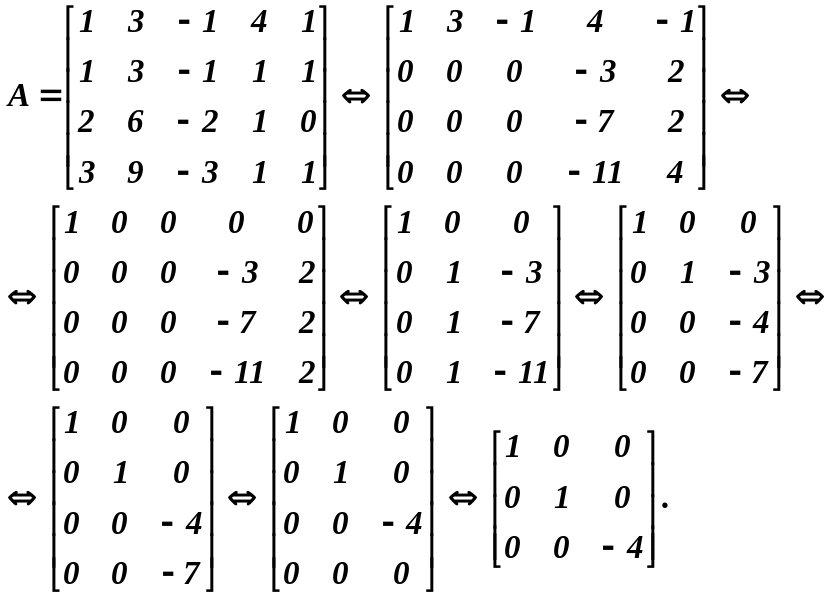
Ранг останньої матриці, а значить, і еквівалентної їй матриці дорівнює 3 ( і менший, ніж число невідомих, а тому вихідна система має ненульові розв’язки. Візьмемо ті рівняння заданої системи, в яких коефіцієнти при невідомих утворюють базисний мінор, наприклад:

який відмінний від нуля.

Задана система лінійних рівнянь еквівалентна такій:

Розв’яжемо її, відносно невідомих , методом Гаусса. Виключимо в другому і третьому рівняннях

Виключимо в третьому рівнянні

Із останнього рівняння знаходимо, що , а значить, і (із другого рівняння). З першого рівняння одержимо

Таким чином,

При довільних значеннях вільних невідомих та одержимо відповідні значення базисних невідомих. Наприклад, один із часткових розв’язків такий:

ТЕОРЕМА. Якщо визначник (1.9) системи лінійних однорідних алгебраїчних рівнянь з невідомими дорівнює нулю, а серед алгебраїчних доповнень А_ij ( елементів го рядка є ненульові, то ця система має ненульовий розв’язок: x_j=А_ij∙t. (1.10)

Тут t- деякий параметр.

Доведення. Підставивши розв’язок (1.10) в систему рівнянь (1.8) при , одержимо:

при (за теоремою анулювання);

при (за умовою теореми).

Приклад 3. Розв’язати систему лінійних однорідних рівнянь

Розв'язування. Визначник

Знайдемо алгебраїчні доповнення до елементів, наприклад, першого рядка:

Задана система лінійних однорідних алгебраїчних рівнянь має розв’язок

який залежить від параметра